<< 3. Астрономические системы координат | Оглавление | 3.2. Экваториальная система координат >>

3.1. Горизонтальная система координат

Представим себе наблюдателя, находящегося на поверхности Земли. Одним из выделенных направлений для него, как говорилось выше, является направление, совпадающее с отвесной линией, или с силой притяжения Земли. Мысленно продолжим отвесную линию вверх и вниз до пересечения ее с небесной сферой. 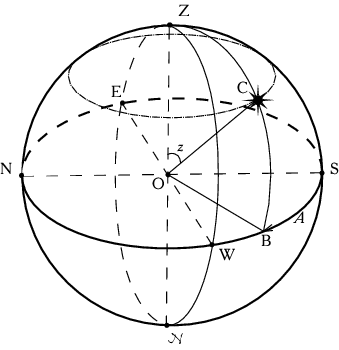Точки пересечения (полюсы горизонтальной системы координат) называются зенитом и надиром и обозначаются как и , соответственно (рис. 3.1). Плоскость, перпендикулярная отвесной линии, называется плоскостью горизонта.

Если через точки зенита и надира провести плоскость, то она пересечет небесную сферу по окружности, которая, по традиции, называется вертикальным кругом. На плоскости горизонта выделим четыре точки: севера (), юга (), запада () и востока () (рис. 3.1). Определение точек севера и юга связано с направлением оси вращения Земли (см. §3.2).

Если вертикальный круг проходит через небесный объект , то он называется вертикалом этого объекта. Дуга вертикала называется зенитным расстоянием объекта . Вместо зенитного расстояния часто используется другая координата: высота объекта над горизонтом; дуга равна . Из рисунка видно, что . Зенитное расстояние (или высота небесного объекта) является одной из координат в горизонтальной системе. Если небесный объект находится над горизонтом, то его зенитное расстояние изменяется от (объект в зените) до (объект в плоскости горизонта). Высота объекта изменяется от до , соответственно. Если или , то говорят, что объект находится под горизонтом; он в этом случае невидим для наблюдателя^3.3. При или объект находится в надире. При таком определении зенитного расстояния угол эквивалентен углу (см. определение сферических координат (§2.3) и рис. 2.5).

Второй координатой в горизонтальной системе является азимут небесного объекта. Азимут -- это двугранный угол между плоскостью и вертикалом объекта. Следует заметить, что в определении начальной точки отсчета азимута имеется произвол. В учебнике К.А.Куликова "Курс сферической астрономии" и некоторых других учебниках азимут отсчитывается от точки юга в направлении на запад (по часовой стрелке) от до . В данном учебнике также принимается это соглашение. В ряде книг азимут отсчитывается от точки севера на восток от до , а иногда азимут измеряется в пределах .

Главными кругами в горизонтальной системе координат являются: плоскость горизонта, первый вертикал, вертикал небесного тела и точки : зенита, надира, севера, юга, востока и запада. Используются также малые круги светил -- круги высоты или альмукантараты. Это -- круги, параллельные плоскости горизонта и проходящие через небесного тело. На рис. 3.1 круг высоты показан пунктирной линией.

Допустим, что наблюдатель неподвижен относительно горизонтальной системы координат. Из-за того, что направление отвесной линии не совпадает с направлением оси вращения Земли (если наблюдатель не находится на полюсе), объекты на небе движутся относительно горизонтальной системы сложным образом: одновременно меняются и зенитное расстояние, и азимут. Поэтому, чтобы звезда сохраняла свое положение в поле зрения телескопа, телескоп должен также перемещаться по сложному закону.

---

<< 3. Астрономические системы координат | Оглавление | 3.2. Экваториальная система координат >>

Публикации с ключевыми словами: астрометрия - сферическая астрономия - системы координат - шкалы времени Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени
См. также: Достижения космической астрометрии Скончался Константин Владиславович Куимов Константину Владиславовичу Куимову – 75 лет Саймон Ньюком (1835 -1909) к 175-летию со дня рождения. Вращение Земли и продолжительность суток 80 лет со дня рождения Альберта Петровича Гуляева Руководство по практической работе с каталогом Hipparcos Все публикации на ту же тему >>