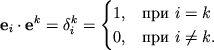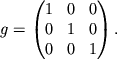2.3. Сферическая система координат
Для решения многих задач оказывается удобнее вместо декартовой
системы использовать криволинейные системы координат. В общем
случае используются три функции
![]() ,
,
![]() ,
,
![]() для определения положения тела в пространстве.
Координатная сетка состоит из пересекающихся кривых
для определения положения тела в пространстве.
Координатная сетка состоит из пересекающихся кривых
![]() вместо сетки прямых линий
вместо сетки прямых линий
![]() в
декартовой системе. Если функции выбраны подходящим образом, то
положение объекта может быть однозначно определено с
помощью криволинейных координат
в
декартовой системе. Если функции выбраны подходящим образом, то
положение объекта может быть однозначно определено с
помощью криволинейных координат
![]() вместо декартовых
координат
вместо декартовых
координат ![]() .
.
К таким системам относится и сферическая система
координат, широко
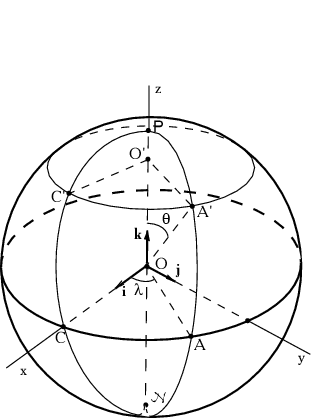
используемая не только в астрономии, но и других науках.
Сферические координаты (см. рис. 2.5): ![]() --
радиус-вектор объекта,
--
радиус-вектор объекта, ![]() -- полярное
расстояние, которое иногда называют
коширотой, и
-- полярное
расстояние, которое иногда называют
коширотой, и ![]() -- долгота связаны с декартовыми координатами
-- долгота связаны с декартовыми координатами
![]() уравнениями:
уравнениями:
Полярное расстояние изменяется от
Система уравнений (2.20) представляет преобразование между
сферической и декартовой системами координат. Следовательно,
функции
![]() равны:
равны:
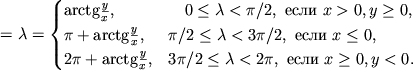 |
Вернемся к рис. 2.5. Через произвольно выбранные точки ![]() и
и ![]() проведем большой круг. Полюсы обозначим как
проведем большой круг. Полюсы обозначим как ![]() и
и ![]() .
Проведем теперь через полюсы и точку
.
Проведем теперь через полюсы и точку ![]() большой круг (аналогично
проведем большой круг через точку
большой круг (аналогично
проведем большой круг через точку ![]() ). Обозначим через
). Обозначим через ![]() центральный угол между направлением на точку
центральный угол между направлением на точку ![]() и направлением на
произвольную точку
и направлением на
произвольную точку ![]() , лежащую на сфере в плоскости большого
круга
, лежащую на сфере в плоскости большого
круга ![]() . Проведем через точку
. Проведем через точку ![]() плоскость,
параллельную большому кругу
плоскость,
параллельную большому кругу ![]() . Полученная плоскость является
малым кругом, и радиус
. Полученная плоскость является
малым кругом, и радиус ![]() окружности равен, если
окружности равен, если
![]() :
:
Введем декартову систему координат: ось ![]() направим вдоль радиуса
направим вдоль радиуса
![]() , ось
, ось ![]() -- вдоль радиуса
-- вдоль радиуса ![]() . Обозначим единичные векторы
осей
. Обозначим единичные векторы
осей ![]() и
и ![]() как
как ![]() и
и ![]() , соответственно. Направление
оси
, соответственно. Направление
оси ![]() зададим единичным вектором
зададим единичным вектором ![]() согласно уравнению:
согласно уравнению:
Векторное произведение (2.22) векторов
Обозначим через ![]() двугранный угол между плоскостями
двугранный угол между плоскостями
![]() и
и ![]() . Числа
. Числа
![]() называются
сферическими координатами точки
называются
сферическими координатами точки ![]() . При
. При ![]() достаточно
знать две координаты
достаточно
знать две координаты
![]() для определения положения
точки на сфере. В следующей главе будут определены различные
системы сферических координат. В каждой из них координаты
для определения положения
точки на сфере. В следующей главе будут определены различные
системы сферических координат. В каждой из них координаты
![]() имеют разные названия и могут обозначаться другими
буквами.
имеют разные названия и могут обозначаться другими
буквами.
Пусть точка ![]() лежит на сфере и является точкой пересечения
большого круга
лежит на сфере и является точкой пересечения
большого круга ![]() и малого круга
и малого круга ![]() (рис. 2.5). Найдем длину дуги
(рис. 2.5). Найдем длину дуги
![]() . Так как
центральный угол
. Так как
центральный угол ![]() равен
равен ![]() , то
, то
Рассмотрим более подробно вопрос преобразования координат вектора в криволинейных координатах.
В криволинейной системе координат в отличие от декартовой
возможны два способа выбора базисной тройки векторов: 1) базисные
векторы являются касательными в точке
![]() к кривым
к кривым
![]() ,
,
![]() ,
,
![]() ; обозначим их как
; обозначим их как
![]() ,
,
![]() ,
,
![]() и 2) базисные векторы
перпендикулярны в точке
и 2) базисные векторы
перпендикулярны в точке
![]() к поверхностям,
задаваемым функциями
к поверхностям,
задаваемым функциями
![]() , т.е.
, т.е.
![]() ,
,
![]() ,
,
![]() ; обозначим их как
; обозначим их как
![]() ,
,
![]() ,
,
![]() . Еще одним отличием от
декартовой системы является то, что направление, а также длина
базисных векторов может различаться в разных точках пространства.
. Еще одним отличием от
декартовой системы является то, что направление, а также длина
базисных векторов может различаться в разных точках пространства.
В случае сферических координат поверхность, задаваемая уравнением
![]() , есть сфера радиуса
, есть сфера радиуса ![]() , уравнение
, уравнение
![]() определяет малый круг, а
определяет малый круг, а
![]() -- плоскость меридиана. Пересечения
этих плоскостей со сферой являются окружностями. Так как кривые
-- плоскость меридиана. Пересечения
этих плоскостей со сферой являются окружностями. Так как кривые
![]() ,
,
![]() ,
,
![]() также являются
окружностями, то в случае сферических координат обе базисные
тройки совпадают. В общем случае это не так.
также являются
окружностями, то в случае сферических координат обе базисные
тройки совпадают. В общем случае это не так.
Два выбора базисных троек дают возможность найти проекции вектора
![]() как на оси
как на оси
![]() ,
,
![]() ,
,
![]() ,
так и на оси
,
так и на оси
![]() ,
,
![]() ,
,
![]() :
:
индексы суммирования могут обозначаться любыми буквами.
Числа
![]() называются
контравариантными, а
называются
контравариантными, а
![]() --
ковариантными проекциями
вектора
--
ковариантными проекциями
вектора
![]() .
.
Для базисных векторов
![]() справедливы
соотношения:
справедливы
соотношения:
Символ
Скалярное произведение в криволинейных координатах записывается в виде
Для того, чтобы получить явное выражение ковариантных и
контравариантных координат вектора, умножим скалярно первое из
уравнений (2.24) на
![]() , а второе -- на
, а второе -- на
![]() . Учитывая определение (2.25), найдем:
. Учитывая определение (2.25), найдем:
Значит,
Используя формулы (2.26), перепишем (2.24) в виде:
Соотношения справедливы для любого вектора
![]() . Если вместо
. Если вместо
![]() в (2.27) подставить базисные векторы, то получим:
в (2.27) подставить базисные векторы, то получим:
Вводя обозначения
перепишем соотношения (2.28) таким образом:
Для построения базисной тройки
![]() по векторам
по векторам
![]() необходимо знать матрицу с элементами
необходимо знать матрицу с элементами ![]() ; и,
наоборот, для построения базиса
; и,
наоборот, для построения базиса
![]() по базису
по базису
![]() -- матрицу с элементами
-- матрицу с элементами ![]() . Эти матрицы
взаимно обратны, т.е.
. Эти матрицы
взаимно обратны, т.е.
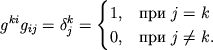
Величины ![]() и
и ![]() называются компонентами дважды
контравариантного и ковариантного метрического
тензора, соответственно.
называются компонентами дважды
контравариантного и ковариантного метрического
тензора, соответственно.
Что из себя представляет тензор в математике? Как мы видели, задание базисной тройки определяет систему координат, в которой можно найти координаты произвольных векторов, т.е. их проекции на базисные векторы. Но так как при переходе в другую точку пространства направление и величина базисных векторов может меняться, то необходимо решить задачу о преобразовании проекций произвольных векторов из одной базисной тройки в другую. Эта задача решается методами тензорного анализа. Тензоры представляют собой систему величин, преобразующихся по линейному закону при переходе от одной системы координат к другой. Соотношения, записанные в тензорной форме, сохраняют свою форму в любой координатной системе.
Найдем теперь расстояние
![]() между двумя бесконечно
близкими точками пространства. Декартовы координаты вектора
между двумя бесконечно
близкими точками пространства. Декартовы координаты вектора
![]() равны
равны ![]() . Для этого, считая
. Для этого, считая ![]() в
формулах (2.20) функциями переменных
в
формулах (2.20) функциями переменных
![]() найдем
дифференциалы
найдем
дифференциалы ![]() ,
, ![]() ,
, ![]() . По правилу вычисления
дифференциалов функций многих переменных, сначала фиксируем
переменные
. По правилу вычисления
дифференциалов функций многих переменных, сначала фиксируем
переменные
![]() и находим изменение функции (частную
производную
и находим изменение функции (частную
производную
![]() ) в зависимости от приращения
) в зависимости от приращения ![]() ,
затем фиксируем переменные
,
затем фиксируем переменные ![]() и
и ![]() и находим изменение
функции в зависимости от приращения
и находим изменение
функции в зависимости от приращения ![]() , и наконец при
постоянных
, и наконец при
постоянных ![]() и
и ![]() находим частную производную
находим частную производную
![]() . В результате получим:
. В результате получим:
По определению частные производные
![]() и др. являются касательными к
функциям
и др. являются касательными к
функциям ![]() , т.е. представляют собой компоненты базисных
векторов
, т.е. представляют собой компоненты базисных
векторов
![]() ,
,
![]() ,
,
![]() вдоль
направлений
вдоль
направлений
![]() :
:
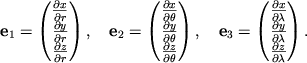
Следовательно, дифференциал функции является контравариантным
вектором. Переобозначив бесконечно малые приращения как
![]() ,
, ![]() ,
, ![]() , найдем квадрат расстояния
, найдем квадрат расстояния ![]() между двумя бесконечно близкими точками, который равняется в
декартовой системе координат
между двумя бесконечно близкими точками, который равняется в
декартовой системе координат
В более общем виде с учетом правила суммирования выражение для квадрата расстояния между двумя точками пространства записывается в виде:
где
Выбор той или иной системы координат дает возможность определить положение тела в пространстве и упростить уравнения движения тела, но не определяет свойства самого пространства. Задание метрики совместно с определением системы координат полностью описывает пространство. Это означает, что, зная метрический тензор, можно вычислить расстояние между двумя точками. В случае евклидова пространства, которое называется плоским, расстояние находится по формуле (2.32) и метрический тензор равен
В случае плоского пространства метрический тензор
Если пространство не является плоским, то для вычисления расстояний уже нельзя использовать закон Пифагора (2.32). В частности, при вычислениях на сфере (в кривом пространстве) длина дуги между двумя точками не равна длине хорды (расстоянию в плоском пространстве).
Квадрат элемента длины в сферической системе координат легко
найти, вычислив частные производные
![]() и т.д. и подставив их
в (2.32). Используя уравнения (2.20), находим, что
и т.д. и подставив их
в (2.32). Используя уравнения (2.20), находим, что
![]() ,
,
![]() и т.д. В результате
после приведения подобных членов получим, что
и т.д. В результате
после приведения подобных членов получим, что
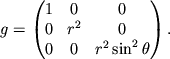
Таким образом, свойства геометрии в криволинейной системе
координат определяются компонентами ![]() метрического
тензора. В дальнейшем мы будем рассматривать четырехмерное
пространство-время для вычисления эффектов теории относительности
(изменения хода часов, находящихся в гравитационном поле,
отклонения луча света). В четырехмерном пространстве-времени
имеется, следовательно, 16 компонент тензора, из них только 10
различны из-за симметричности тензора (четыре с одинаковыми
индексами и
метрического
тензора. В дальнейшем мы будем рассматривать четырехмерное
пространство-время для вычисления эффектов теории относительности
(изменения хода часов, находящихся в гравитационном поле,
отклонения луча света). В четырехмерном пространстве-времени
имеется, следовательно, 16 компонент тензора, из них только 10
различны из-за симметричности тензора (четыре с одинаковыми
индексами и ![]() с различными индексами).
с различными индексами).
<< 2.2. Скаляры, векторы, тензоры | Оглавление | 2.4. Основные формулы сферической >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |