Разделы
- 2.1. Регенеративные спирали Линден-Белла
- 2.2. Энтузиазм MIT
- 2.3. Гравитационная устойчивость плоских систем
- 2.4. Калнайс в поиске спиральных мод
2. На гребне новой волны
| Если вы хотите узнать у физиков-теоретиков что-нибудь о методах, которыми они пользуются, советую вам твердо придерживаться следующего принципа: не слушайте того, что они говорят, а лучше изучайте их работы. |
А. Эйнштейн [88]
2.1. Регенеративные спирали Линден-Белла
| Мы находим, что в нашей Галактике спиральные рукава существуют на протяжении большей части ее жизни и что старые рукава закручиваются, поэтому из их останков должны образовываться новые, еще незакрученные рукава. Проблему описания такого механизма мы называем проблемой регенерации. |
Д. Линден-Белл [90]
В 1960 г. Линден-Белл представил диссертацию "Звездная и галактическая динамика" [89], в которой рассмотрел ряд общих вопросов звездной динамики и эргодической теории. Отдельная ее часть - "космогоническая динамика газа" - была посвящена проблеме спиральной структуры. В ней констатировалось, что "рукава - это прежде всего сосредоточение газа и пыли" (ввиду отсутствия которых в линзовидных галактиках "спиральная структура образовываться уже не может"), и перспективным поэтому виделся космогонический подход, но при условии отказа от классической схемы Джинса как совершенно непригодной в условиях дифференциального вращения.
"Представляется невозможным, чтобы протогалактический газ вращался однородно на стадии образования звезд. Вероятно, когда первичный газ разбивался на сгущения [протогалактики], каждый жидкий элемент стремился сохранить свой момент вращения около центра местного сгущения. В результате достигалось состояние равновесия, в котором центробежная и гравитационная силы практически компенсировали друг друга, а давление главным образом препятствовало образованию слишком тонкой системы" [89].
Линден-Белл рассмотрел реалистичные равновесные конфигурации невязкой газовой системы и вывел "энергетический принцип, который должен стать мощным средством определения равновесий на компьютере". По достижении одного из равновесных состояний система вступает в этап вековой эволюции. "Ее будет определять не сжатие, связанное с излучением энергии, как у Джинса, а перенос углового момента, обусловленный трением". Система "должна i) собрать момент в очень малой части своей массы и ii) перевести оставшуюся массу в более плотное состояние, поддерживаемое однородным вращением или давлением, - в соответствии с данными по солнечной системе и галактикам". "Таким образом, нам следует ожидать возникновения однородно вращающегося центрального сгущения, окруженного дифференциально вращающимся диском" [89].
Именно с таким диском газа Линден-Белл соотнес возможность
спиралеобразования. В сдвиговой деформации - прямой угрозе любой
возникающей структуре - он, в отличие от большинства других
исследователей, видел не антагониста "дилеммы сохраняемости"
спиральных рукавов, а фактор их циклического
воспроизводства, обусловленного гравитационной неустойчивостью
газовой компоненты в едином звездно-газовом диске галактик
(звездное население, по Линден-Беллу, обеспечивало равновесие
системы газа, но в общей коллективной динамике не участвовало). В
такой постановке задача предполагала полный анализ устойчивости в
условиях дифференциального вращения, что было невыполнимо
технически. Поэтому, за неимением лучшего, были использованы
методы, которые Фрике применял к модели газового слоя с
![]() [64]. Это привело к необходимому и достаточному
условию джинсовской устойчивости
[64]. Это привело к необходимому и достаточному
условию джинсовской устойчивости
![]() ,
36
а также определило инкремент
неустойчивости как величину
,
36
а также определило инкремент
неустойчивости как величину
![]() . Наиболее важной - спадающей к центру и к краю диска,
длинноволновой и потому быстрорастущей - становилась мода
. Наиболее важной - спадающей к центру и к краю диска,
длинноволновой и потому быстрорастущей - становилась мода ![]() при
при
![]() . Это по сути была
линдбладовская бар-мода (см. рис. 2) с двумя сгущениями по разные
стороны от центра на расстоянии
. Это по сути была
линдбладовская бар-мода (см. рис. 2) с двумя сгущениями по разные
стороны от центра на расстоянии ![]() кпк, она определяла
начальную стадию неустойчивости. Пока плотность возмущения
нарастала в
кпк, она определяла
начальную стадию неустойчивости. Пока плотность возмущения
нарастала в ![]() раз, вращение поворачивало моду на 180o (при
раз, вращение поворачивало моду на 180o (при
![]() . Но сдвиговые движения (в анализе
устойчивости неучтенные) за это время успевали закрутить ее в
полный виток спирали. Это означало уменьшение длины волны, и, как
ожидалось, должно было вызывать уменьшение
. Но сдвиговые движения (в анализе
устойчивости неучтенные) за это время успевали закрутить ее в
полный виток спирали. Это означало уменьшение длины волны, и, как
ожидалось, должно было вызывать уменьшение ![]() и устранение
неустойчивости; рукава спирали в таком случае рассасывались, и
восстанавливался "слой, с которого мы начинали", так что весь
процесс мог повторяться. Однако более тщательный анализ
подтвердил зависимость
и устранение
неустойчивости; рукава спирали в таком случае рассасывались, и
восстанавливался "слой, с которого мы начинали", так что весь
процесс мог повторяться. Однако более тщательный анализ
подтвердил зависимость ![]() от
от ![]() только "для систем, очень
близких к устойчивости". Такое условие было "слишком
чувствительным для объяснения всего многообразия спиралей", оно не
могло выполняться повсеместно, "в любой части наблюдаемых
спиральных рукавов". Следовательно, заключил сам автор, его
регенеративная теория в предложенном виде "неприменима"
[89].
только "для систем, очень
близких к устойчивости". Такое условие было "слишком
чувствительным для объяснения всего многообразия спиралей", оно не
могло выполняться повсеместно, "в любой части наблюдаемых
спиральных рукавов". Следовательно, заключил сам автор, его
регенеративная теория в предложенном виде "неприменима"
[89].
Действительно, полагаясь в своих регенеративных начинаниях на сдвиговые эффекты, Линден-Белл по сути просто наложил последние на самосогласованную динамику твердотельно вращающегося диска. Возможные динамические - коллективные - проявления сдвигового диска автоматически оказывались при этом вне рассмотрения. И все же пессимизм Линден-Белла был чрезмерным. Как в результате выяснилось, его регенеративные идеи содержали немалую долю истины. Но все это пришло не сразу и не по прямой дороге, потому что, как мы увидим в следующем разделе, старая идея установившихся спиральных мод вот-вот была готова была вызвать новый взрыв энтузиазма.
2.2. Энтузиазм MIT
Цзя-Цзяо Линь астрономом не был. С довоенного времени предмет его исследований составляли течения жидкостей. К началу 60-х гг. он имел более 60 публикаций, монографию по теории гидродинамических неустойчивостей [90], мировую известность эксперта по прикладным наукам и должный авторитет на отделении математики Массачусетсского технологического института (MIT), где он работал с 1947 г. Тем не менее, определенное отношение к астрономии у Линя было. К работам Чандрасекара, математической строгостью которых он восхищался, к исследованиям М.Шварцшильда по физике звезд, к морфологическому методу Цвики. С 1961 г. этот интерес стал жизненно важной необходимостью. Весной того года Линь приехал в Принстон к Стремгрену (для обсуждения с ним своих наработок по жидкому гелию в контексте строения звезд [91,92]), и там он принял участие в уже известной нам конференции по межзвездной среде. Ознакомившись с текущей ситуацией в изучении галактик, он проникся живым интересом к проблеме сохраняемости их спиральных форм37.
По возвращении в MIT Линь передал свой галактический энтузиазм молодым сотрудникам Хантеру и Томре38. Для оперативного знакомства с текущей периодикой была создана "группа чтения"39, в атмосфере дружелюбной общительности" [85] проходили частые дискуссии и организованные Линем рабочие визиты Волтьера и Люста40; на отделение был принят Лебовиц41. В 1962 г. к Линю для выполнения курсовой работы пришел студент Шу42, а Хантер и Томре, чьи контракты завкончились, уехали: один назад в Кембридж, другой в Принстон; в 1963 г. вышли их первые работы.
Дебют Томре и Хантера в динамике галактик был связан с насущной
задачей, уже поставленной, но не решенной сколько-нибудь
основательно [95,96]: как соотнести эмпирические кривые
вращения галактик с равновесным распределением в них массы? Томре
[97] развил общий математический метод решения задачи и для
модели бесконечно тонкого диска получил серию решений, ныне
известных как модели Томре n-го порядка [102, c.
44]43 Хантер [99], решая задачу в иной аппроксимации
тонкого диска, получил другую серию точных решений. Самой простой
в ней оказалась хорошо известная модель твердотельно вращающегося
диска с профилем поверхностной плотности
![]() . Только она
позволяла исследовать устойчивость равновесия
аналитически, и Хантер выполнил эту задачу, доказав "с помощью
ручки, бумаги и полиномов Лежандра" [30, c. 464], что
холодный диск такого типа неустойчив по
отношению к целому набору осесимметричных и неосесимметричных
колебательных мод.44.
Эти две работы Томре и Хантера
проложили дорогу дальнейшим исследованиям кинематических моделей и
глобальной динамики плоских звездных систем.
. Только она
позволяла исследовать устойчивость равновесия
аналитически, и Хантер выполнил эту задачу, доказав "с помощью
ручки, бумаги и полиномов Лежандра" [30, c. 464], что
холодный диск такого типа неустойчив по
отношению к целому набору осесимметричных и неосесимметричных
колебательных мод.44.
Эти две работы Томре и Хантера
проложили дорогу дальнейшим исследованиям кинематических моделей и
глобальной динамики плоских звездных систем.
2.3. Гравитационная устойчивость плоских систем
| Линь спросил [Волтьера в 1961]: "Какие нужны были бы обстоятельства для того, чтобы звездная и межзвездная части предположительно гладкого диска галактики оставались гравитационно устойчивыми - по отдельности или вместе - относительно любых крупномасштабных возмущений?" |
A. Tомре [101, с. 1217]
| Томре первым ясно указал на важность коллективных эффектов в нашей Галактике. Он показал, что движения звезд в диске достаточно связаны для того, чтобы диск оказался почти не защищенным от разрушения. |
А. Калнайс [83, c. 275]
Как мы помним, Сафронов уже ставил вопрос о гравитационной неустойчивости плоских вращающихся газовых систем, имея в виду разбиение протопланетного облака на отдельные кольца. Томре в 1961 г. обратился к близкой по сути, но противоположной по направленности, задаче и к лету 1963 г. подготовил статью "О гравитационной устойчивости диска звезд" ([101], в дальнейшем Т64)45.
Работа начиналась с общего представления проблемы, каковой она тогда виделась:
"Факт известных неустойчивостей сфероидов Маклорена, вращательное сжатие которых превышает определенное - весьма умеренное - значение, наводит на мысль о возможности неустойчивости и в других случаях вращающихся самогравитирующих систем при достаточной степени их сплюснутости. Во всяком случае, об этих неустойчивостях часто говорят как о вероятной причине ненаблюдаемости сильно сплюснутых эллиптических галактик. И только когда мы обращаемся к рассмотрению характера распределений всех - за исключением самых молодых - звезд в дисках обычных (без перемычек) спиральных галактик, этот классический результат приводит к серьезной дилемме : как объяснить то, что, несмотря на эти или аналогичные им неустойчивости, столь большая часть звездной материи в таких галактиках - и, очевидно, в S0-галактиках - распределена сейчас сравнительно плавно в дисках со степенью сжатия примерно 10:1?" [101, с. 1217]
Детальному изучению проблемы был предпослан первичный, качественный анализ устойчивости.
Тонкий холодный диск, находящийся в примерном равновесии между
гравитационной и центробежной силами, действующими на любой
элемент массы, удерживается от общего сжатия, но не от
фрагментации. Мелкомасштабные сгущения, повсеместно образующиеся
в таком диске, коллапсируют, поскольку избыток их гравитации
превосходит избыток вращения. Но на больших масштабах они не
идут, потому что соотношение тех же двух факторов становится
обратным. Критический масштаб ![]() , разделяющий устойчивый и
неустойчивый режимы, оказывается порядка радиуса диска
, разделяющий устойчивый и
неустойчивый режимы, оказывается порядка радиуса диска ![]() . Это
значит, что холодный диск, какой бы конкретной моделью он ни
описывался, крайне неустойчив46.
Вклад тепловых движений лучше всего
иллюстрирует модель покоящегося слоя. Гравитационная
неустойчивость в нем предотвращается, если слагающие его звезды
(или другие элементы) при характерной случайной скорости
. Это
значит, что холодный диск, какой бы конкретной моделью он ни
описывался, крайне неустойчив46.
Вклад тепловых движений лучше всего
иллюстрирует модель покоящегося слоя. Гравитационная
неустойчивость в нем предотвращается, если слагающие его звезды
(или другие элементы) при характерной случайной скорости ![]() проходят область сгущения за время, не превышающее то, в течение
которого при
проходят область сгущения за время, не превышающее то, в течение
которого при ![]() плотность возрасла бы в
плотность возрасла бы в ![]() раз.
Максимальный размер неколлапсирующего сгущения определяется,
таким образом, величиной порядка
раз.
Максимальный размер неколлапсирующего сгущения определяется,
таким образом, величиной порядка
![]() /
/![]() ; это по сути джинсовский критерий устойчивости. Переходя теперь
к вращающемуся слою, мы видим, что критичными становятся обе
характерные величины
; это по сути джинсовский критерий устойчивости. Переходя теперь
к вращающемуся слою, мы видим, что критичными становятся обе
характерные величины ![]() и
и ![]() . С ростом дисперсии
скоростей
. С ростом дисперсии
скоростей ![]() все более приближается к
все более приближается к ![]() и совпадает
с ней, когда
и совпадает
с ней, когда ![]() сравнивается со скоростью вращения по
порядку величины:
сравнивается со скоростью вращения по
порядку величины:
![]() . Наступает полная
стабилизация диска относительно возмущений рассмотренного типа
(рис. 5) [101].
. Наступает полная
стабилизация диска относительно возмущений рассмотренного типа
(рис. 5) [101].
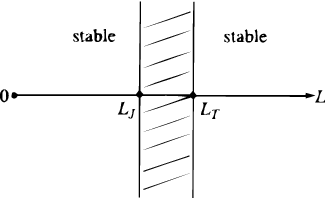
|
|
Рис. 5. Характерные масштабы в гравитирующем диске. По оси отложен размер L радиальных возмущений. Холодный вращающийся диск устойчив для возмущений в области L>lLT, горячий невращающийся слой устойчив для возмущенй в области L<LJ. Горячий врщающийся диск сочетает оба эти условия, поэтому область гравитационной неустойчивости ограничивается интервалом LJ<L<LT. С ростом дисперсии скоростей звезд LJ подтягивается к LT, интервал между ними сужается и при некотором значении c=V (см. текст) исчезает: диск становится полностью устойчивым относительно возмущений рассмотренного типа. |
Количественный анализ осесимметричных возмущений в бесконечно тонком диске, проведенный в работе Т64, подтвердил эти примерные оценки устойчивости. В холодном случае он привел к локальному дисперсионному соотношению
или
в котором
![]() - частота волны в
единицах
- частота волны в
единицах ![]() , а
, а
- критическое волновое число, определяющее минимальную
длину волны
![]() ненарастающих
(
ненарастающих
(![]() 0) возмущений47,
(рис. 6). Для горячего
диска была установлена минимальная радиальная дисперсия скорости,
при которой система все еще остается устойчивой относительно
всех осесимметричных возмущений48
0) возмущений47,
(рис. 6). Для горячего
диска была установлена минимальная радиальная дисперсия скорости,
при которой система все еще остается устойчивой относительно
всех осесимметричных возмущений48![]() 49
49 ![]() (Рис. 7):
(Рис. 7):
 |
 |
|
|
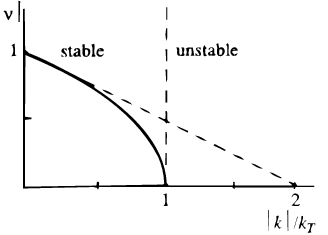
Рис. 6. График дисперсионного соотношения радиальных колебаний
и тугозакрученных спиральных волн в холодном диске.
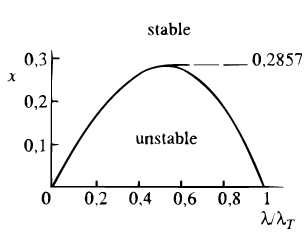
Рис. 7. Кривая нейтральной устойчивости горячего диска
[101]. | ||
Отношение реальной дисперсии к данному минимуму,
задало параметр локальной устойчивости диска50![]() 51.
При маржинальной устойчивости,
51.
При маржинальной устойчивости,
![]() , критическими становились возмущения масштаба
, критическими становились возмущения масштаба
![]() , которым в солнечной окрестности
соответствовала бы величина
, которым в солнечной окрестности
соответствовала бы величина ![]() кпк. Однако наблюдения
говорили в пользу определенного запаса локальной устойчивости,
кпк. Однако наблюдения
говорили в пользу определенного запаса локальной устойчивости,
![]() . Это, конечно, "не отрицало возможности
неустойчивости вообще", но в любом случае речь заведомо не шла бы
о раскачке волн длиной
. Это, конечно, "не отрицало возможности
неустойчивости вообще", но в любом случае речь заведомо не шла бы
о раскачке волн длиной
![]() кпк, которые "практически
наверняка устойчивы". "Это важный аргумент против предположений о
том, что существующая спиральная структура нашей Галактики могла
бы быть результатом коллективных звездных
неустойчивостей рассматриваемого типа" [101, c.
1236].
кпк, которые "практически
наверняка устойчивы". "Это важный аргумент против предположений о
том, что существующая спиральная структура нашей Галактики могла
бы быть результатом коллективных звездных
неустойчивостей рассматриваемого типа" [101, c.
1236].
Вместе с тем, развитая линейная теория не претендовала на многое. Она не могла, например, прояснить причину разогрева звездного диска и даже не показывала с какой-либо ясностью, что должно происходить с начальными сгущениями, возникающими в холодном диске за время всего одного-двух оборотов. "Ни откуда не следует, что такие первоначальные сгущения будут неминуемо приводить к образованию каких-нибудь перманентных иррегулярностей, - заметил Томре. - Гораздо вероятнее, что причастные к любой (в общем случае, неосесимметричной) неустойчивости звезды ... в конце концов разойдутся, выступая из противоположных сторон образования и испытывая вдобавок сдвиговое действие дифференциального вращения".
"Следовательно, первоначально неустойчивый диск звезд должен был уже претерпеть не один, а несколько последовательных этапов неустойчивости, после каждого из которых система становилась несколько менее неустойчивой, чем раньше. В частности, представляется вероятным, что по прошествии очень большого числа оборотов диск мог приблизиться к новому равновесному состоянию, регулярному и, по всей видимости, осесимметричному, в котором тепловые скорости на различных радиусах стали (и, значит, останутся) примерно равными минимальным значениям, требуемым для полной устойчивости" [101, c. 1237]52.
Кроме того, поскольку полная гравитационная энергия диска должна сохраняться по ходу его эволюции (теорема вириала), "указанное перераспределение звезд не могло состоять только из общего сжатия, оно должно было вызывать сжатие внутренних областей диска при одновременном расширении его внешних частей" [109, c. 1237] - как это уже предсказывал в рамках газодинамики Линден-Белл [89].
В отношении неосесимметричных возмущений в работе Т64
было замечено, что в силу специфики кориолисова действия они
сдерживаются легче чисто радиальных и потому большего значения
![]() не требуют. Однако, добавил Томре, его работа
оставляла "полностью открытым" вопрос о возможности стабилизации в
диске с
не требуют. Однако, добавил Томре, его работа
оставляла "полностью открытым" вопрос о возможности стабилизации в
диске с ![]() "наиболее крупных неосесимметричных возмущений
- таких, прежде всего, по которым можно было бы сказать, станет
ли развиваться в данном диске бароподобная структура или нет"
[101, c. 1235]53.
"наиболее крупных неосесимметричных возмущений
- таких, прежде всего, по которым можно было бы сказать, станет
ли развиваться в данном диске бароподобная структура или нет"
[101, c. 1235]53.
2.4. Калнайс в поиске спиральных мод
| По-моему, можно провести параллель между сегодняшними попытками вести разговор о развитии галактик и попытками понять звездную эволюцию до того как были поняты источники энергии звезд. |
Дж. Р. Бербидж [51, c. 291]
| Изучение звездных систем, подобных нашей Галактике, ограничено не недостатками понимания лежащих в их основе принципов, а скорее трудностью решения описывающих их эволюцию дифференциальных уравнений. |
А. Калнайс [105, с. i]
Агрис Калнайс поступил в электротехническую школу MIT в 1955г. За успехи в учебе он был зачислен в группу углубленного изучения физики и математики, в составе которой проходил практику в лаборатории микроволновых исследований в Рейтоне, где проводил измерения для компьютерного моделирования магнетронов. Здесь он узнал о движении электронов в перекрестных электрических и магнитных полях, о параметрическом усилении, о волнах положительной и отрицательной энергии, о волновых модах. Все это пригодилось ему в самостоятельной работе, правда в совсем ином направлении, когда в 1959 г. он пришел на астрономическое отделение Гарвардского университета и обратился к динамике галактик54.
Осенью 1961 г. Калнайс выполнил исследовательскую работу "Звездная
кинематика" [106]55.
Задача
состояла в расчете самосогласованных радиальных колебаний во
вращающемся звездном диске с целью объяснения ими 'местных'
рукавов Галактики. Малость межрукавного расстояния, ![]() кпк,
оправдывала локальный анализ возмущений в плоскости
тонкого однородного слоя. В рамках задачи на начальные условия
Калнайс решил уравнения Власова и Пуассона56,
получив уравнение осесимметричных
колебаний и корректное дисперсионное соотношение общего вида.
Интересуясь, однако, коротковолновыми решениями, он произвел
асимптотический анализ интегрального выражения, по ходу которого
упустил "множитель
кпк,
оправдывала локальный анализ возмущений в плоскости
тонкого однородного слоя. В рамках задачи на начальные условия
Калнайс решил уравнения Власова и Пуассона56,
получив уравнение осесимметричных
колебаний и корректное дисперсионное соотношение общего вида.
Интересуясь, однако, коротковолновыми решениями, он произвел
асимптотический анализ интегрального выражения, по ходу которого
упустил "множитель ![]() или около того" [105]. Это, а
также заниженный отклик диска на столь короткие (
или около того" [105]. Это, а
также заниженный отклик диска на столь короткие (
![]() 1 кпк) волны, привело к выводу о практическом
совпадении частоты колебаний слоя
1 кпк) волны, привело к выводу о практическом
совпадении частоты колебаний слоя ![]() с частотой колебаний
звезд
с частотой колебаний
звезд ![]() . "Эффекты самогравитации на коротких масштабах
волн слишком малы, чтобы представлять какой-либо интерес", -
заключил Калнайс [105]; все решения осциллируют и
описывают бегущую от центра волну, которая прибирает по пути
"объекты низкой дисперсии, такие как газ" [106, c. ii]. В
качестве возможного волнового генератора допускалось овальное
тело в центре Галактики.
. "Эффекты самогравитации на коротких масштабах
волн слишком малы, чтобы представлять какой-либо интерес", -
заключил Калнайс [105]; все решения осциллируют и
описывают бегущую от центра волну, которая прибирает по пути
"объекты низкой дисперсии, такие как газ" [106, c. ii]. В
качестве возможного волнового генератора допускалось овальное
тело в центре Галактики.
Ошибка асимптотического анализа вскрылась летом 1963 г., когда Калнайс и Томре наконец встретились. Сравнив и проверив свои расчеты, они нашли друг у друга технические недочеты. Калнайс пересмотрел свою теорию радиальных колебаний и произвел перерасчет дисперсионного соотношения, получив его на этот раз в том виде, в котором оно вошло в его диссертацию 1965 г. [107]57. В современных обозначениях, удобством и ясностью которых мы, несомненно, обязаны Линю, а также без поправки за тощину звездного диска, содержавшейся в расчетах 1961-63 гг., но не представляющей особого интереса58, это соотношение имет вид
где
- калнайсов вариант множителя, учитывающего роль тепловых движений звезд.
Эти движения отсутствуют в пределе ![]() , когда равенство (9) сводится к
равенству Томре (5) для холодного диска, устанавливающему пропорциональность
гравитационного члена волновому числу и, соответственно, его неограниченный
рост. Тепловые движения этот рост сдерживают. Теперь вклад гравитации лишь
достигает максимума при
, когда равенство (9) сводится к
равенству Томре (5) для холодного диска, устанавливающему пропорциональность
гравитационного члена волновому числу и, соответственно, его неограниченный
рост. Тепловые движения этот рост сдерживают. Теперь вклад гравитации лишь
достигает максимума при ![]() , а для
, а для ![]() он становится
малым. В солнечной окрестности уровню
он становится
малым. В солнечной окрестности уровню ![]() соответствует длина волны
соответствует длина волны
![]() кпк, установленная Томре при анализе маржинальной
устойчивости. Ее соизмеримость с радиусом диска Галактики делает локальную
теорию весьма сомнительной.
кпк, установленная Томре при анализе маржинальной
устойчивости. Ее соизмеримость с радиусом диска Галактики делает локальную
теорию весьма сомнительной.
"Выполняя в 1961 свою исследование, я находился под впечатлением
того, что расстояние между рукавами спирали составляет 1.5 кпк.
После встречи с Томре мне стало ясно, что волны (флуктуации)
такого масштаба важных для Галактики мод не представляли. ...
К тому же, к осени 1963 г. я получил копию диссертации Денвера.
Его измерения спиральных рукавов галактик давали типичный угол
закрутки
![]() , что означало еще большие, чем
6 кпк, масштабы. ...Томре к этому времени уже опубликовал
свои дисковые модели, и я мог использовать их для оценки
масштаба, на котором диски откликаются сильнее всего. Я убедился
в том, что ВКБ-приближение [см. раздел 3.1] слишком грубое и что
галактики, в отличие от плазмы, слишком неоднородные. Будущее
поэтому виделось за глобальными модами и интегральными
уравнениями" [105].
, что означало еще большие, чем
6 кпк, масштабы. ...Томре к этому времени уже опубликовал
свои дисковые модели, и я мог использовать их для оценки
масштаба, на котором диски откликаются сильнее всего. Я убедился
в том, что ВКБ-приближение [см. раздел 3.1] слишком грубое и что
галактики, в отличие от плазмы, слишком неоднородные. Будущее
поэтому виделось за глобальными модами и интегральными
уравнениями" [105].
Осознав этот факт, Калнайс потерял интерес к локальным теориям, полезным лишь для устойчивых коротковолновых решений, и обратился к глобальным модам: в них он видел теперь залог корректного решения проблемы. Уже в октябре 1963 г. им был представлен "Набросок диссертации на тему 'Спиральная структура галактик' ", содержавший наработки для новой теории установившихся спиральных волн. Ввиду фактической неизвестности этой работы, следующая большая цитата из нее [109, с. 1-3] представляется уместной59.
"Особенность, присущая сильно сплюснутым системам, состоит в наличии у них спиральных указателей, называемых рукавами. Эти образования наиболее рельефно прослеживаются по газовой компоненте галактик и по молодым горячим звездам, которые возбуждают газ. Однако флуктуации плотности заметны и в звездной компоненте, где они гораздо слабее, но, в то же время, и регулярнее.
Деление галактики на две компоненты, газовую и звездную, представляется вполне естественным при рассмотрении динамического поведения этих подсистем. Газовая компонента частично ионизована и, следовательно, подвержена и магнитной, и гравитационной силам; она также очень неравномерно распределена в галактической плоскости. Звездная же система довольно регулярна, ее динамика управляется дальнодействующими гравитационными силами со стороны галактики как целого, при этом концентрация звезд достаточно низка для того, чтобы двойными звездными сближениями можно было пренебрегать. Будучи массивной, звездная компонента не может поддерживать флуктуации плотности на масштабах, много меньших среднего отклонения звезд от круговых орбит (масштаб пекулярных движений). Зато газ мог бы поддерживать флуктуации меньшего масштаба, по крайней мере, в отсутствии магнитных эффектов. То что наблюдаемые рукава не намного уже минимального масштаба, который могут допускать звезды, говорит об активном участии последних в создании спиральных узоров.
Имеется, однако, фундаментальная проблема, связанная с предположением о том, что спиральные рукава сложены целиком из звезд. Если рукав существует и не нарастает со временем, то его зеркальное отражение - тоже возможная конфигурация: это следует из обратимости во времени уравнений движения и из инвариантности относительно пространственной обратимости. Поэтому на основе линейной теории нельзя установить лидирующий или отстающий характер рукавов, если настаивать на постоянстве формы спиральных указателей. В то же время наблюдения указывают, что природа отдает предпочтение отстающим спиральным руавам. Следовательно, правдоподобная теория спиральной структуры должна включать и звезды, и газ.
Я рассматриваю галактику состоящей из двух компонент, газа и звезд, связанных силами гравитации. Звезды обеспечивают крупномасштабную организацию, а газ позволяет отличать отстающие рукава от лидирующих. (Звездная система может рассматриваться как резонатор; газ тогда будет генератором, возбуждающим некоторые нормальные моды). Если связь [газовой и звездной компонент] не слишком сильна, то сначала обе подсистемы можно рассматривать отдельно, а потом допустить их взаимодействие. К сожалению, оценить степень этой связи без расчета нормальных мод обеих подсистем нельзя. Для газовой компоненты в настоящее время возможен только самый грубый анализ, поскольку для правдоподобности результатов в уравнениях движения газа необходимо учитывать нелинейные члены. Напротив, звездная компонента довольно гладкая, и для нее можно использовать линейную теорию. Так что можно поставить и - при небольших усилиях - решить задачу об определении нормальных мод.
В качестве темы своей диссертации я выбрал исследование звездных нормальных мод в плоскости модельной галактики. ...Некоторые качественные особенности уравнений указывают на то, что предпочтительным оказывается тип спиральных возмущений с двумя рукавами. Этот результат, очевидно, не сильно зависит от выбора модели, что немаловажно. Окончательное доказательство остается за численными расчетами, которые пока не завершены". [106, c. 1-3]
Можно, таким образом, видеть, что звездный диск галактики представлялся Калнайсу резонатором, в котором развиваются глобальные спирально-волновые моды. В стационарном случае отстающие и лидирующие волны являются зеркальным отражением друг друга, поэтому при сложении не дают общей спиральной картины. Симметрию, однако, нарушают необратимые процессы, присущие реальным галактикам.
В поддержку своей концепции нормальных мод Калнайс рассмотрел
крупномасштабные неосесимметричные возмущения в горячем неоднородном плоском
диске и вывел для них общее интегральное уравнение, частотная зависимость
которого предполагала дискретный волновой спектр. Он отметил также важную роль
линдбладовского условия (4). При его выполнении значительная область
галактического диска может поддерживать когерентные колебания для моды ![]() , тогда как для любых значений
, тогда как для любых значений ![]() > 2 внутрь диска попадают линдбладовские резонансы. Звезды,
двигаясь в области этих резонансов, испытывают возмущающее действие волны с
частотой их собственных колебаний,
> 2 внутрь диска попадают линдбладовские резонансы. Звезды,
двигаясь в области этих резонансов, испытывают возмущающее действие волны с
частотой их собственных колебаний,
и, как следствие, претерпевают сильные смещения на
своих орбитах, из-за чего в итоге моды ![]() теряют вид единой
цельной спирали60.
Калнайс заключил, что сформулированная
им проблема говорит, таким образом, о предпочтительности
двухрукавных спиралей и "дает скупое понимание того, что можно
ожидать при
теряют вид единой
цельной спирали60.
Калнайс заключил, что сформулированная
им проблема говорит, таким образом, о предпочтительности
двухрукавных спиралей и "дает скупое понимание того, что можно
ожидать при ![]() в плане формы возмущений и их зависимости от
времени" [109, с. 13].
в плане формы возмущений и их зависимости от
времени" [109, с. 13].
Обощающим изложением рассмотренных Калнайсом проблем стала его диссертация "Устойчивость сильно уплощенных галактик", представленная им в мае 1965 г. в Гарварде [107]61. Она содержала развернутую дискуссию на базе детального математического анализа. Вместе с тем, диссертация по сути явилась официальным публичным дебютом Калнайса, поэтому именно с ней следует соотносить хронологию событий, связывая те или иные фактические моменты спиральной истории 1960-х гг.
<< 1. Эпоха Линдблада | Оглавление | 3. Теория Линя >>
|
Публикации с ключевыми словами:
история астрономии - спиральная галактика - волны плотности - спиральная структура
Публикации со словами: история астрономии - спиральная галактика - волны плотности - спиральная структура | |
См. также:
Все публикации на ту же тему >> | |
