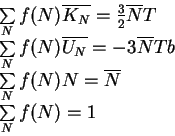Энтропия большого канонического ансамбля в расширяющейся Вселенной
<< 1. Вступление | Оглавление | 3. Модельный конфигурационный интеграл >>
2. Энтропия
Пусть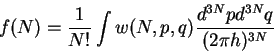 |
(1) |
Наша задача сейчас состоит в том, чтобы получить выражение для
энтропии через величины ![]() . Определение энтропии следующее:
. Определение энтропии следующее:
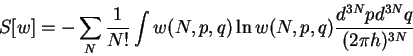 |
(2) |
где
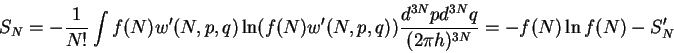
а величины
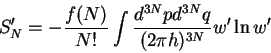 |
(3) |
Здесь делается второе предположение. Релаксация по энергии уже произошла, а по числу частиц - нет. Это разумно, так как первое происходит на расстоянии, в то время как второе связано с физическим перемещением галактик. Характерное время релаксации по числу частиц поэтому порядка размера рассматриваемого объема, деленного на среднюю "тепловую" скорость частиц. Для релаксации же по энергии характерное время есть скорость частицы, деленная на вызываемое другими галактиками ускорение. Для скопления галактик, содержащего в объеме 5 Мпк несколько сотен галактик, с "тепловыми" скоростями около двух-трех сотен километров в секунду они оказываеются порядка соответственно 10 и 1 миллиардов лет, так что релаксация по энергии происходит значительно раньше.
Релаксация и максимизация энтропии для нас - одно и то же. Поэтому
надо максимизировать величины ![]() . Теперь время вспомнить о
налагаемых на ансамбль условиях. Обычно, учитывая уравнение Лиувилля, ищут
зависимость от интегралов движения, и добавляя соображения о необходимости
аддитивности последних, получают распредения Гиббса. Однако последние не
кажутся очевидными для гравитационно связанных систем. Ни откуда не следует,
что фиксируется суммарная энергия. Поэтому естественным кажется включение
ограничений по отдельности на число частиц, кинетическую и потенциальную
энергию, причем под последней имеется в виду именно энергия корреляций - то
есть разница между реализуемой при данной конфигурации
. Теперь время вспомнить о
налагаемых на ансамбль условиях. Обычно, учитывая уравнение Лиувилля, ищут
зависимость от интегралов движения, и добавляя соображения о необходимости
аддитивности последних, получают распредения Гиббса. Однако последние не
кажутся очевидными для гравитационно связанных систем. Ни откуда не следует,
что фиксируется суммарная энергия. Поэтому естественным кажется включение
ограничений по отдельности на число частиц, кинетическую и потенциальную
энергию, причем под последней имеется в виду именно энергия корреляций - то
есть разница между реализуемой при данной конфигурации ![]() и средней в
данном объеме. Запишем эти условия, которые, собственно и выделяют системы и
условия полной нормировки:
и средней в
данном объеме. Запишем эти условия, которые, собственно и выделяют системы и
условия полной нормировки:
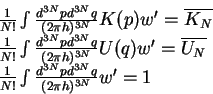 |
(4) |
Максимизируя
| (6) |
Далее из
![]() легко получить:
легко получить:
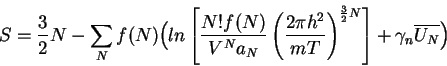 |
(7) |
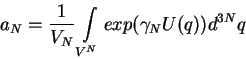
Для ![]() имеем уравнение:
имеем уравнение:
| (8) |
Итак, мы получили выражение для энтропии как функции ![]() и
и
![]() .
.
<< 1. Вступление | Оглавление | 3. Модельный конфигурационный интеграл >>
|
Публикации с ключевыми словами:
Космология - галактики - Расширение Вселенной - гравитационное скучивание галактик - термодинамика - энтропия
Публикации со словами: Космология - галактики - Расширение Вселенной - гравитационное скучивание галактик - термодинамика - энтропия | |
См. также:
Все публикации на ту же тему >> | |