Астронет > Вариационные принципы в физике

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Вариационные принципы в физике

Е. Д. Трифонов

Российский государственный педагогический университет им. А.И. Герцена, Санкт-Петербург

Теперь остается только подобрать радиус окружности для того, чтобы циклоида прошла через вторую заданную точку B. Все циклоиды подобны друг другу. Поэтому Бернулли предложил следующее построение. Построим какую-нибудь циклоиду, исходящую из первой точки A. Построим прямую, проходящую через обе заданные точки A и B. Эта прямая пересечет построенную циклоиду в некоторой точке О (рис. 3, а). Радиус окружности для искомой циклоиды относится к радиусу построенной циклоиды как отрезок AB к отрезку AO. Интересно, что в некоторых случаях для быстрейшего достижения конечной точки оказывается выгодным предварительно опуститься ниже ординаты этой точки (рис. 3, б).

Циклоида как форма траектории обладает еще одним замечательным свойством, открытым Гюйгенсом. Время движения тела по циклоиде под действием собственной тяжести до нижней ее точки не зависит от начального положения тела и превышает время падения с высоты h = d в p $\pi/2$ раз.

Заметим, что решение данной задачи И. Бернулли основано на кинематической оптико-механической аналогии, отличной от динамической аналогии, которая рассматривалась нами в статье [2]. Она носит чисто кинематический характер. Далее перейдем к выводу вариационных принципов механики, основанных на динамической оптико-механической аналогии.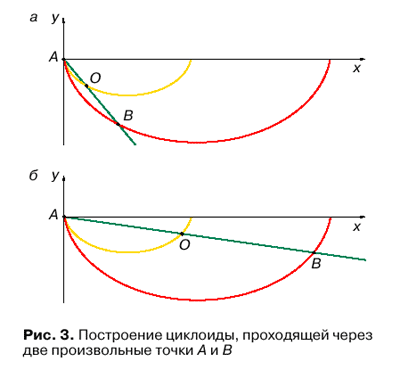

Принцип наименьшего действия Мопертюи

Напомним, что динамическая оптико-механическая аналогия состоит в том, что траектория материальной точки при движении ее в потенциальном поле U(x, y, z) и траектория луча в оптически неоднородной среде с непрерывно изменяющимся показателем преломления n(x, y, z) в точности совпадают, если выполняется соотношение пропорциональности

$$n(x,y,z)~v(x,y,z)=\sqrt{\frac{2}{m}(E-U(x,y,z))},$ (7)$

где m - масса материальной точки, u(x, y, z) - абсолютная величина ее скорости, Е - энергия. При этом направление скорости в начальной точке совпадает с направлением луча.

Воспользуемся опять принципом Ферма. Запишем время распространения света вдоль луча. С этой целью разобьем луч, соединяющий две фиксированные точки, на N достаточно малых отрезков $\Delta q_i$ , i=1,...,N. Показатель преломления среды на каждом из отрезков обозначим через n_i . Тогда скорость света на отрезке $\Delta q_i$ будет c/n_i , где c - скорость света в вакууме. Время распространения света вдоль этого отрезка равно $\Delta q_in_i/c$ . Тогда полное время распространения света вдоль луча можно представить в виде суммы

$$t=\frac{1}{c}\sum\limits^N_{i=1}n\Delta q_i.$ (8)$

Согласно принципу Ферма, эта сумма, вычисленная для истинного хода луча, должна быть минимальной по сравнению с такими же суммами для любой достаточно близкой вымышленной или, как говорят, виртуальной формы луча, проходящего через те же две точки.

Поскольку ход луча совпадает с траекторией движения материальной точки при определенном соответствии, выражаемом формулой (7), между потенциальным полем и показателем преломления, то очевидно, что аналогичный вариационный принцип должен выполняться и в механике. Подставляя в (8) вместо показателя преломления n_i абсолютное значение скорости материальной точки, умноженное на массу, получим, что величина

$$W=\sum\limits^N_{i=1}mv_i\Delta q_i$ (9)$

для истинной траектории, соединяющей две заданные точки, принимает минимальное значение по сравнению со значением этой величины, вычисленной для близкой виртуальной траектории, проходящей через те же две точки.

Величину W, стоящую в левой части (9), называют в механике действием, а сформулированный выше вариационный принцип, выражаемый этой формулой, - принципом наименьшего действия Мопертюи, поскольку в такой форме он впервые (1740) был предложен французским академиком Пьером Мопертюи (1698-1759). Интересно, что это было сделано при очень смутных представлениях об оптико-механической аналогии и явилось скорее счастливой догадкой, основанной на теолого-философских воззрениях автора. Аргументируя справедливость высказанного им принципа, Мопертюи почти точно повторяет слова Ферма: "Природа в своих действиях всегда пользуется наиболее простыми средствами". Возникли горячие дискуссии о справедливости этого принципа (в которых принял участие даже Вольтер), а затем не менее горячие споры о приоритете открытия. Из современников лишь Леонард Эйлер (1707-1783) поддержал Мопертюи, доказав справедливость его принципа на конкретных примерах.

Принцип наименьшего действия Гамильтона

Следующий важный шаг в развитии вариационных принципов был сделан Уильямом Гамильтоном (1805-1865) (с биографией и творческой жизнью Гамильтона можно познакомиться по книге [7]).

Гамильтон предложил новую форму вариационного принципа механики. Мы проиллюстрируем вариационный принцип Гамильтона на примере материальной точки, движущейся в потенциальном поле, не зависящем от времени. В этом случае выполняется закон сохранения энергии, то есть сумма кинетической и потенциальной энергии не изменяется со временем:

$$E=\frac{m(v^2_x+v^2_y+v^2_z)}{2}+U(x,y,z)=const,$ (10)$

хотя координаты и составляющие скорости частицы являются функциями времени: x = x(t), y = y(t), z = z(t), u_x = u_x(t), u_y = u_y(t), u_z = u_z(t). Пусть частица движется так, что в начальный момент времени t = 0 она находится в точке с координатами x₀ , y₀ , z₀ , а в момент времени t = T - в точке с координатами x₁ , y₁ , z₁ .

Разобьем траекторию движения на интервалы $\Delta q_i$ , которые частица проходит за малые промежутки времени Dti (последние можно считать равными по величине). Тогда скорость на i-м интервале будет $u_i = \Delta q_i/\Delta t_i$ .

Запишем теперь действие для этого движения, прибавив к нему константу -ET. Используя очевидное равенство $\sum\limits_i\Delta t_i = T$ , получим

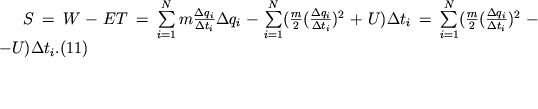
$S=W-ET=\sum\limits^N_{i=1}m\frac{\Delta q_i}{\Delta t_i}\Delta q_i - \sum\limits^N_{i=1}(\frac{m}{2}(\frac{\Delta q_i}{\Delta t_i})^2 + U)\Delta t_i = \sum\limits^N_{i=1}(\frac{m}{2}(\frac{\Delta q_i}{\Delta t_i})^2 - -U)\Delta t_i. (11)$

Введенную таким образом величину S также называют действием, а чтобы не было путаницы, величину W - укороченным действием. Мы видим, что для истинного движения действие S имеет минимальное значение по сравнению с его значениями на виртуальных траекториях, точки которых в начальный и конечный моменты времени совпадают соответственно с начальным и конечным положениями материальной точки.

Хотя это утверждение следует из принципа наименьшего действия Мопертюи, оказалось, что оно имеет большую область применимости и выполняется также для случая, когда потенциальная энергия зависит от времени. Причем при выборе виртуальных координат материальной точки можно не заботиться о сохранении энергии. В тех случаях, когда потенциальная энергия не зависит явно от времени, для истинного движения полная энергия будет сохраняться автоматически. Обратим внимание также на то, что в вариационном принципе Гамильтона можно варьировать (то есть изменять для сравнения величины действия S) не только форму траектории (как в принципе Мопертюи), но и характер движения по ней с течением времени. При этом должно только выполняться условие: полное время движения фиксировано.

Итак, принцип наименьшего действия Гамильтона можно сформулировать следующим образом. Действие S для истинного движения материальной точки, траектория которого в начальный и конечный моменты времени проходит через две определенные точки, принимает минимальное значение по сравнению с любыми виртуальными движениями, траектории которых в указанные моменты времени проходят через те же две точки.

Из-за недостатка места мы не приводим здесь конкретных примеров, подтверждающих справедливость принципов Мопертюи и Гамильтона. Ученику можно рекомендовать самостоятельно убедиться в этом на примере свободного падения тела в однородном поле тяжести. Это можно сделать аналитически, если ученик знаком с интегрированием элементарных функций, или с помощью компьютера, который становится все более доступным для школьного обучения.

Заключение

Кратко остановимся на роли, которую сыграли вариационные принципы в развитии физики.

После формулировки вариационных принципов в форме Мопертюи и Гамильтона были предложены и другие вариационные принципы механики. Их общее значение заключалось в том, что с их помощью удавалось единым методом получать уравнения движения сложных механических систем. (В основной части статьи мы не затрагивали этого важного этапа применения вариационных принципов, поскольку это требует достаточно сложного, и не только для школьников, математического аппарата.) В дальнейшем было показано, что вариационные принципы возможны и в других разделах физики, например в электродинамике и специальной теории относительности.

Вариационные принципы, возникшие из конкретных физических задач, обогатили и саму математику. Одной из общих вариационных задач, появившейся почти одновременно с задачей о брахистохроне, была задача о геодезической линии: требуется найти линию наименьшей длины, соединяющую две заданные точки на некоторой поверхности. Позже эта задача была обобщена на случай многомерных пространств с неевклидовой геометрией и вернулась в физику в общей теории относительности, где роль геодезических в четырехмерном пространстве-времени играют уравнения движения материальной точки. В частности, геодезической с нулевой "длиной" является уравнение движения частицы со скоростью света. Так появился очень важный аспект, связывающий физику и геометрию пространства, которая оказалась зависящей от реального распределения масс.

Вариационные принципы и физическая идея об оптико-механической аналогии имели определяющее значение для рождения волновой и квантовой механики. В этом можно легко убедиться, если заглянуть в оригинальные работы Луи де Бройля и Э. Шрёдингера (см. переводы этих работ в книге [3]). Вариационные принципы применяются и в квантовой теории поля, являющейся базой для исследования элементарных частиц.

Вы видите, что рожденные усилиями гениев вариационные принципы механики и оптики оказали огромное влияние на последующее развитие всей физики, - влияние, простирающееся до наших дней и далеко не исчерпанное.

Литература

1. Ньютон И. Математические начала натуральной философии. М.: Наука, 1989. 688 с.

2. Трифонов Е.Д. Оптико-механическая аналогия в изложении для школьников // Соросовский Образовательный Журнал. 1997. N 10. С. 133-137.

3. Вариационные принципы механики: Сб. ст. / Под ред. Л.С. Полака. М.: Гос. изд-во физ.-мат. лит., 1959. 932 с.

4. Гюйгенс Х. Трактат о свете. М.; Л., 1935.

5. Кудрявцев П.С. История физики. М.: Учпедгиз, 1948. Т. 1. 535 с.

6. Сивухин Д.В. Общий курс физики: Оптика. М.: Наука, 1980. 751 с.

7. Полак Л.С. Уильям Гамильтон. М.: Наука, 1993. 270 с.

Назад | К содержанию

Публикации с ключевыми словами: геометрическая оптика - физика - вариационный принцип
Публикации со словами: геометрическая оптика - физика - вариационный принцип

См. также:

Формула Эйнштейна

Всемирный год физики: триумф Эйнштейна

Внешняя баллистика пневматического оружия

Нобелевская премия по физике за 2004 год

Почему у кошек девять жизней?

Топ-10 по физике в 2003 году

УРАНИЯ Научно-популярный образовательный журнал в "Русском переплете"

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце