Внешняя баллистика пневматического оружия
10.04.2005 23:49 | Astronet

ВОТ ПУЛЯ ПОЛЕТЕЛА ... ВНЕШНЯЯ БАЛЛИСТИКА ПНЕВМАТИЧЕСКОГО ОРУЖИЯ

В своё время один ковбой-философ высказал "мудрую" мысль о том, что кратчайшее расстояние между ним и целью – это пуля. Наверное, он думал о воображаемой прямой линии, соединяющей дуло его кольта 45 калибра с грудью (или головой) своего противника, и эта прямая у него ассоциировалась с пулей.

В чем-то ковбой-философ был почти прав, если учесть, что свои отношения с противником он выяснял на малой дистанции – 5...10 м, и в этом случае действительно траекторию полёта его пули можно приближённо принять как прямую.

На самом деле, после вылета из ствола пуля летит не по прямой, а по некоторой кривой, которая и называется баллистической траекторией. В безвоздушном пространстве баллистическая траектория представляла бы собой параболу, а вот в воздухе, который нас окружает, траектория пули при детальном рассмотрении будет достаточно сложной, не располагающейся в одной плоскости кривой.

Изучением особенностей движения пуль, снарядов (да и вообще любых брошенных тел) занимаются такие интересные науки, как внешняя баллистика, аэродинамика, механика, в частности, такой её мощный раздел как динамика.

При полёте в атмосфере на пулю действуют две основные силы – сила земного притяжения и сила сопротивления воздуха, а также ряд менее значимых сил, например, сила Магнуса, которая в нашем случае, т.е. для пневматики, чаще проявляется при полёте шарообразных пуль, получивших незапланированное вращение в поперечном направлении при вылете из ствола), силы аэродинамического демпфирования (торможения).

Сила притяжения вызывает постепенное снижение пули, а сила сопротивления воздуха (аэродинамическая сила) непрерывно уменьшает скорость пули и заставляет её совершать в целом довольно сложное пространственное движение (о чем разговор пойдет дальше). На траекторию полёта пули также влияют и такие факторы, как метеорологические условия (давление, влажность и температура воздуха, ветер) и начальные возмущения в момент вылета пули из ствола.

Идеальная траектория (почему идеальная, разъяснится далее) полёта пули приведена на рис. 1, с помощью которого также достаточно просто разобраться с терминами, принятыми в стрелковом деле.

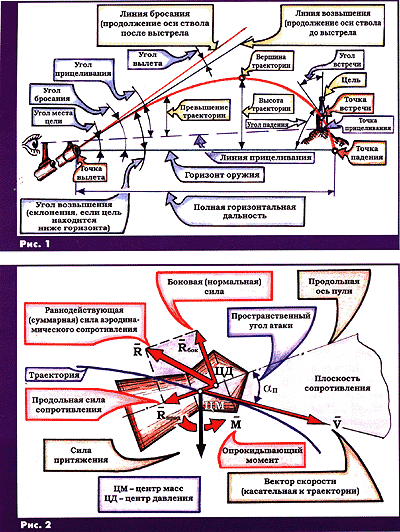К особенностям траектории следует отнести то, что её часть от вершины до точки падения (нисходящая ветвь) короче и круче её части от точки вылета до вершины (восходящая ветвь), а угол падения больше угла бросания; очевидно, что конечная скорость пули всегда меньше начальной, и время полёта по восходящей ветви траектории, естественно, всегда меньше, чем по нисходящей-

А теперь, разобравшись с терминами и определениями, обратимся к рис. 2, на котором приведена схема основных сил, действующих на осесимметричную пулю (в частности, на пневматическую) в полёте. В процессе полёта между продольной осью пули и касательной к траектории (вектором скорости V) существует так называемый пространственный угол атаки α_п, обусловленный действием на пулю начальных возмущений при выстреле, ветра, понижением (отклонением вниз) касательной к траектории.

Сила гравитационного притяжения G приложена в центре масс пули и направлена вниз. Равнодействующая аэродинамическая сила R складывается из сил давления воздуха, направленных по нормали к поверхности пули, и сил трения воздуха об эту поверхность, касательных к ней. Силу R, расположенную в так называемой плоскости сопротивления (т.е. плоскости, проходящей через продольную ось пули и вектор скорости V), можно разложить на две составляющие. Одна из них – продольная сила сопротивления R_прод, расположенная по продольной оси пули в сторону, противоположную её вершине. Вторая – боковая (поперечная, или применительно к рис. 2 – нормальная) сила R_бок, перпендикулярная продольной оси пули и лежащая в плоскости сопротивления.

Аэродинамическая сила R приложена к пуле в точке, которую называют центром давления. Для большинства пневматических пуль, а также и для пуль стрелкового огнестрельного оружия и артиллерийских снарядов центр давления не совпадает с центром масс пули и находится впереди него, т.е. ближе к вершине. В этом случае сила R вызывает аэродинамический момент М, стремящийся увеличить угол атаки, т.е. повернуть пулю вокруг центра масс вершиной назад (опрокидывающий аэродинамический момент).

Такую пулю называют статически (аэродинамически) неустойчивой. Заметим, что существуют и статически устойчивые баллистические объекты, у которых центр давления находится позади центра масс, например, дротики для стрельбы из пневматики, "летающие" шприцы-канюли для дистанционных инъекций животным (да иногда и людям), стрелы для лука, воланчики для бадминтона и, наконец, некоторые крылатые ракеты. У этих объектов центр давления находится позади центра масс (для этого они оснащаются стабилизаторами – кисточкой, юбкой, оперением и т.п.), и аэродинамический момент стремится ликвидировать возникший угол атаки, т.е. совместить продольную ось объекта с вектором скорости (стабилизирующий аэродинамический момент). Изготовлять статически устойчивые пули не всегда возможно, да и не всегда целесообразно по баллистическим соображениям.

И наконец, существуют объекты, которые являются статически нейтральными, например, шар, у которого в идеале центр давления находится в центре масс (в геометрическом центре).

Так как же всё-таки обеспечить движение статически неустойчивых пуль "головой вперёд", т.е. исключить их опрокидывание под действием аэродинамических сил и тем самым получить хорошие кучность и точность стрельбы? Этого можно добиться, придав пуле быстрое вращательное движение вокруг продольной оси (стабилизация вращением). Такое вращение можно осуществить как с помощью тех же аэродинамических сил (например, в турбинных пулях для гладкоствольного оружия), так и более известным для нас способом – с помощью специальных винтовых нарезов в канале ствола, которые в пневматическом оружии используются очень часто, а в огнестрельном оружии (обычном и высокоточном) – сплошь и рядом. Для быстровращающейся пули можно без большой погрешности принять, что её кинетический момент совпадает с продольной осью и направлен в сторону её вершины при правом вращении (по часовой стрелке, если смотреть с донной части) и в сторону донной части при левом. Применительно к гироскопам (а наша пуля – отличный гироскоп) такой кинетический момент называется собственным кинетическим моментом (он определяется как произведение угловой скорости вращения на момент инерции пули относительно продольной оси). И вот такой собственный кинетический момент и "держит" пулю на траектории, не давая ей опрокинуться.

Рассмотрим, как это происходит в случае пули, которая вылетает из ствола "идеально", т.е. без помех. В этом случае в начале полёта продольная ось пули совпадает с вектором скорости (с касательной к траектории), т.е. пространственный угол атаки равен нулю. Аэродинамическая сила направлена по оси пули и просто тормозит её. Затем под действием силы притяжения касательная к траектории начинает понижаться, и появляется угол атаки. Аэродинамическая сила R продолжает тормозить пулю (сила R_прод) и одновременно (сила R_бок) пытается опрокинуть её (на рис. 2 – повернуть против часовой стрелки вокруг центра масс моментом М). А так как пуля обладает собственным кинетическим моментом, появляется компенсирующий гироскопический момент, равный опрокидывающему моменту М, но направленный в противоположную сторону.

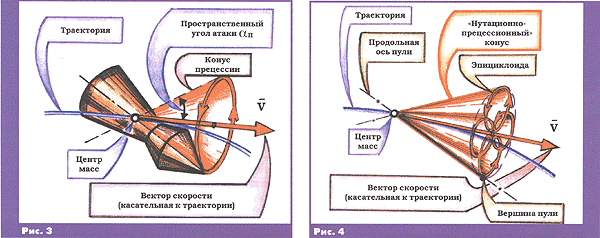
Пуля же в соответствии со свойствами гироскопа начнёт отклоняться не в сторону действия силы, а по направлению, перпендикулярному силе, в данном случае – вправо. Но как только вершина пули начнёт движение вправо, начнёт изменяться положение плоскости сопротивления, т.е. и направление действия составляющей аэродинамической силы R_бок – она начнёт также действовать правее. Вершина пули начнёт уходить вниз, сила R_бок – также вниз и т.д. В результате вершина пули описывает окружность, а её продольная ось – конус с вершиной в центре масс. Такое движение называется прецессионным или просто прецессией (рис. 3). Поскольку угол атаки (полураствор конуса прецессии) достаточно мал, то пуля летит вершиной вперёд. Но это – в идеале, т.е. как было сказано, для полёта пули без начальных помех. На самом деле в момент вылета из ствола, вследствие его вздрагивания (например, от отдачи) и под остаточным действием сжатого газа (воздуха) пуля получает некоторый боковой толчок или импульс. Направление этого толчка, вообще говоря, может быть произвольным. При этих условиях наиболее естественно (как это и принято в стрелковой и артиллерийской практике) полагать, что при вылете из ствола пуля от толчка почти мгновенно получает начальную угловую скорость в поперечном направлении. В связи с этим (и опять-таки в связи со свойствами гироскопа) продольная ось пули начнёт дополнительно совершать радиальное движение (колебания), называемое нутационным или просто нутацией.

В результате (рис. 4) вершина пули начнёт описывать довольно хитрую кривую, называемую эпициклоидой, а продольная ось пули – весьма замысловатый конус с основанием в виде этой самой эпициклоиды. Нутационные колебания постепенно затухают под действием сил аэродинамического демпфирования.

Естественно, на первый взгляд кажется, что упомянутые конусы описываются продольной осью пули вокруг вектора скорости (т.е. вокруг касательной к траектории), что действительно и происходит в самом начале траектории. Но затем касательная к траектории под действием силы притяжения начинает понижаться, и это приводит к тому, что пуля начинает колебаться не относительно вектора скорости, а относительно так называемой динамической оси равновесия, которая отклонена вбок (вправо при правом вращении) от вектора скорости на некоторый угол. Этот угол, в частности, прямо пропорционален скорости вращения пули и крутизне траектории. И вот это самое отклонение вправо динамической оси равновесия от вектора скорости приводит к возникновению добавочного бокового "довеска" к аэродинамической силе, в результате происходит дополнительное перемещение центра масс пули также вправо. Это специфическое явление называется деривацией, которую необходимо учитывать при стрельбе на большие дальности.

Ну, и если быть достаточно скрупулёзным, следует отметить следующее. Угловые прецессионно-нутационные колебания пули вокруг центра масс приводят к тому, что и сам центр масс одновременно с деривационным уходом совершает в поперечной плоскости такие же колебания, т.е. описывает постепенно затухающую эпициклоиду.

Таким образом, траектория пули, как было упомянуто в начале статьи, является действительно сложной кривой: центр масс пули летит вперёд и вправо (деривация), совершая при этом поперечные эпициклоидальные колебания, а сама пуля совершает такие же колебания вокруг центра масс. Однако пусть нас, дорогой читатель, это не смущает: все поперечные колебания пуль пневматического, да и в основном стрелкового огнестрельного оружия, как будет показано ниже, весьма и весьма малы и к тому же постепенно затухают (эти колебания ощутимы в мощной дальнобойной артиллерии), а деривация компенсируется правильной пристрелкой.

Необходимо отметить двойственный характер действия на пулю опрокидывающего момента от аэродинамической силы. С одной стороны, этот момент обусловливает необходимость придания пуле гироскопической устойчивости за счёт вращения, чтобы не допустить её кувыркания (и не ухудшить дальность, точность и кучность стрельбы). С другой стороны, на криволинейном участке траектории вращающаяся пуля "следит" за касательной к траектории только благодаря тому, что на неё действует опрокидывающий момент. Если бы не было этого момента (не было бы воздуха), продольная ось пули (вектор её собственного кинетического момента) при движении по траектории перемещалась бы плоскопараллельно и сохраняла бы начальную ориентацию в пространстве, полученную при вылете из ствола (т.е. пуля могла бы попасть в цель под большим углом, а то и вообще почти боком).

Мы всё время говорим о вращении пули, и возникает естественный вопрос, с какой угловой скоростью её вращать. Не влезая в густые дебри механики, аэродинамики, теории устойчивости отметим, что выбор скорости вращения осуществляется по двум критериям. Первый критерий задаёт нижнее, допустимое для обеспечения устойчивости пули, значение угловой скорости, исходя из соотношений моментов инерции пули относительно продольной и поперечной осей, её начальной скорости, площади поперечного сечения, расстояния между центром масс и центром давления (плеча аэродинамической силы), некоторых аэродинамических коэффициентов. Второй критерий определяет верхнюю границу скорости вращения, исходя из минимизации угла отклонения динамической оси равновесия от вектора скорости: устойчивая вращающаяся пуля должна "следить" за касательной к траектории, поэтому допускать больших отклонений динамической оси не следует (т.е. нельзя чрезмерно увеличивать скорость вращения). Эта граница определяется устойчивым движением пули в вершине траектории, т.е. в критической точке, где наблюдается перегиб. Тут возможен казус – нижняя граница превосходит верхнюю: это происходит при очень больших углах бросания (больше 70 град.), свойственных мощной дальнобойной артиллерии. В этом случае приходится искать другие способы обеспечения стабилизации снарядов (например, с помощью оперения).

Так как мы стреляем из пневматики по очень настильным траекториям (в большинстве случаев с углами бросания менее 10 град.), то для нас "перестабилизация" пули вращением не страшна, особенно, если цель поражается на восходящей ветви траектории (а часто так и бывает). При этом, поскольку для каждого калибра пневматики существует целая гамма пуль с разной степенью статической неустойчивости (которая определяется отношением разности расстояний от вершины пули до центра масс и центра давления к ее длине), разбросом массо-габаритных характеристик и т.п., фирмы-производители оружия обычно выпускают универсальные стволы с повышенной крутизной нарезов для гарантированной устойчивости даже самых неустойчивых пуль. Поэтому скорость вращения пули выбирается с достаточно большим запасом – на 25...50% больше минимально допустимого значения.

Заданная угловая скорость вращения пули обеспечивается с помощью нарезов в стволе. Длина хода их равна линейной (дульной) скорости пули, поделенной на скорость вращения (угловую скорость) и умноженной на 2π. Если длину хода нарезов поделить на калибр ствола, то получим длину хода нарезов в калибрах (более универсальный параметр).

Необходимо вкратце упомянуть о влиянии на полёт пули метеоусловий. Нормальные метеоусловия -это температура воздуха +15 С, давление 750 мм рт. ст., влажность 50%, ветер отсутствует. Изменение метеоусловий напрямую влияет на плотность воздуха, т.е. и на пропорциональную ей аэродинамическую силу, которая действует на пулю.

Так, повышение атмосферного давления, влажности и понижение температуры приводит к увеличению плотности воздуха (и, в результате, к уменьшению дальности полёта пули) и наоборот. Ветер влияет на полёт пуль опять-таки через ту же самую аэродинамическую силу. Если ветер попутный или встречный, то соответственно убывает или возрастает продольная сила сопротивления, а значит, возрастает или уменьшается дальность полёта пули.

Боковой ветер приводит к появлению дополнительного угла атаки в боковой плоскости, т.е. к возрастанию боковой составляющей аэродинамической силы и, соответственно к отклонению пули в ту сторону, куда дует ветер. Применительно к пневматике отметим, что сильный (скорость 6...8 м/с) и умеренный (4...5 м/с) ветер существенно влияет на лёгкую пулю, имеющую малую поперечную нагрузку (отношение массы пули к площади её поперечного сечения) и относительно небольшую скорость.

Таковы вкратце теоретические основы полёта пули. Здесь мы умышленно не говорим о таких разделах внешней баллистики как рассеивание, пристрелка оружия и т.п., так как они достаточно полно изложены в доступных наставлениях по стрелковому делу.

Поговорим лучше немного о практической стороне полёта пули (а то теоретические "зёрна" – это всё изящная словесность, а ведь нужно что-то и поклевать).

Рассмотрим типовую пневматическую пулю типа "дьябло" Gamo Hunter калибра 4,5 мм с куполообразной головкой, обладающую довольно высокой кучностью и сохраняющей максимум энергии на больших дальностях.

Усреднённые данные по такой пуле следующие: масса ~0,47 г (7,25 гран); длина ~5,7 мм; диаметр головной части 4,5 мм, диаметр юбки – 4,7 мм; расстояние центра масс от вершины ~2,73 мм, а центра давления ~2,4 мм (пуля имеет малую статическую неустойчивость - 5,8%).

Остальными параметрами (такими, например, как моменты инерции пули, её аэродинамические коэффициенты) не будем перегружать читателя, и отвлекать его от главного – увидеть в цифрах поведение пули в полёте.

Пусть пуля выстреливается из компрессионного пистолета многоразовой накачки Crosman 1377 калибра 4,5 мм с длиной ствола 250 мм и длиной хода правых нарезов 500 мм. Средняя начальная скорость пули при 10 нагнетаниях составляет около 168 м/с. Рассматриваемый ствол сообщает пуле угловую скорость вращения ~2111 с^-1, т.е. ~336 об/с. Минимальная требуемая скорость для такой пули из условия обеспечения гироскопической устойчивости составляет ~1505 с^-1 (240 об/с), так что коэффициент запаса по скорости вращения для нашей пули составляет примерно 1,4.

Принимаем, что при вылете из ствола пуля получает достаточно жёсткие для пневматики начальные условия – начальная угловая скорость в поперечном направлении составляет 50 град/с (разброс начальных угловых скоростей в поперечном направлении для стрелкового оружия составляет 30...60 град/с, а в пневматике может быть ещё меньше, в зависимости от типа оружия, прикладки стрелка и т.п.).

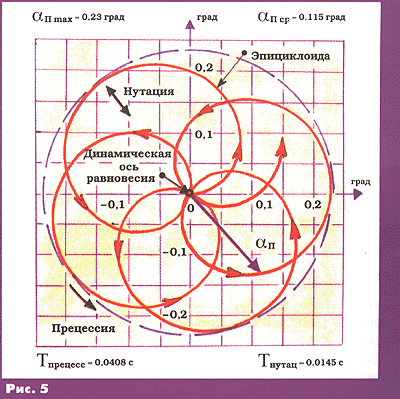На рис. 5 по результатам расчётов приведена иллюстрация углового движения вершины пули относительно динамической оси равновесия в проекции на поперечную плоскость (пуля летит на наблюдателя).

Максимальное значение пространственного угла атаки при заданных начальных условиях составляет ~0,23 град., среднее значение ~0,115 град, (малюсенькая величина, почти нуль!). Динамическая ось равновесия отклоняется от вектора скорости на максимальный угол – 0,043 град, (настолько мало, что можно считать, что пуля колеблется вокруг вектора скорости). При этом период прецессии составляет ~ 0,0408 с, а нутации соответственно ~0,0145 с. Таким образом, наша (хотя по происхождению испанская) пуля совершает весьма резвые угловые колебания по очень маленькой эпициклоиде, да ещё очень быстро крутится вокруг продольной оси. Отметим, что центр масс пули также описывает в поперечной плоскости микроскопическую эпициклоиду с максимальным радиусом ~0,05 мм (считаем, что наша пуля летит плавно) и теми же временными характеристиками, что и у углового движения. Деривация пули при стрельбе на 10 м составляет всего около 1,8 мм (хотя уже есть что компенсировать при пристрелке!). Что можно сказать об этих малых величинах? Маленькая пуля – и всё остальное маленькое.

А теперь в заключение приведём несколько простых приближённых соотношений, позволяющих (если, конечно, есть интерес) "на коленке" рассчитать некоторые основные усреднённые параметры траектории при настильной стрельбе пулями типа "дьябло" калибра 4,5 мм с массой 0,50,1 г. Напомню, что под "дьяволом" подразумевается пуля с ярко выраженной головной частью любой из известных форм (плоская, куполообразная, полусферическая или конусная) и "юбкой" (с насечкой или без).

Здесь: V₀ – дульная скорость (м/с); L – дальность стрельбы (м); ω₀ – угловая скорость вращения пули вокруг продольной оси (с ).

У некоторых читателей может появиться недоумение по поводу размерностей в формулах, но здесь нет ошибки – ВСЁ учтено в цифровых коэффициентах.

Таково краткое, очень краткое, описание процесса полёта пневматической пули.

(Статья перепечатана из журнала "Пневматическое оружие в России", N 3, 2003.)

Публикации с ключевыми словами: физика Публикации со словами: физика
См. также: Формула Эйнштейна Всемирный год физики: триумф Эйнштейна Нобелевская премия по физике за 2004 год Почему у кошек девять жизней? Топ-10 по физике в 2003 году УРАНИЯ Научно-популярный образовательный журнал в "Русском переплете" Физика и астрономия Все публикации на ту же тему >>