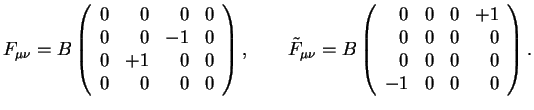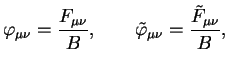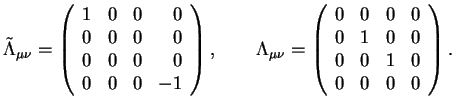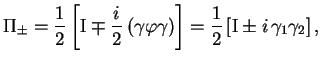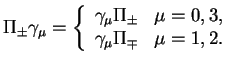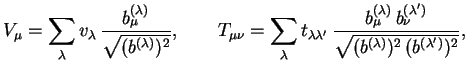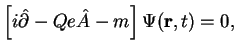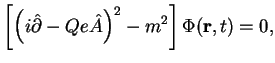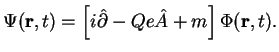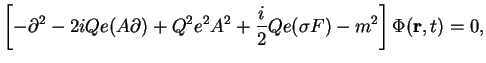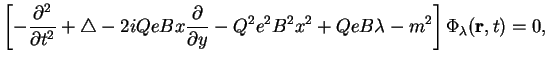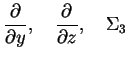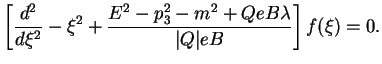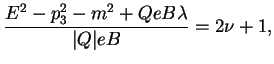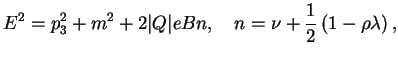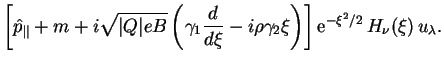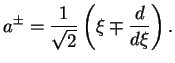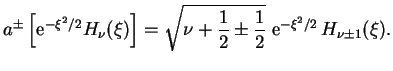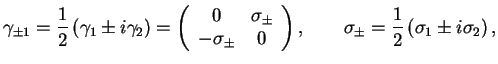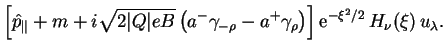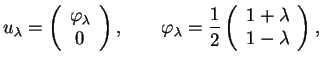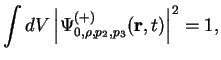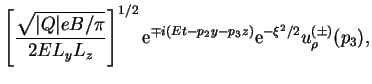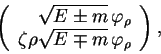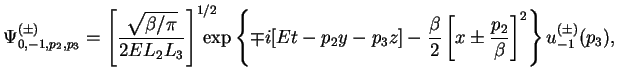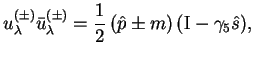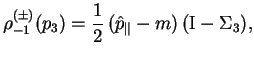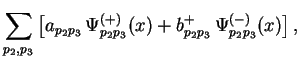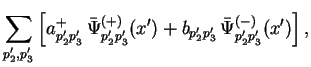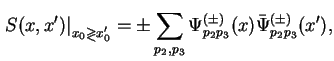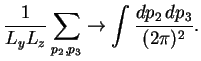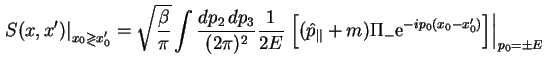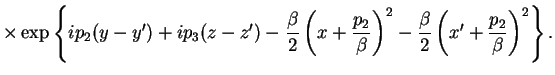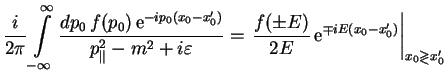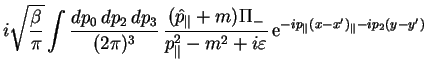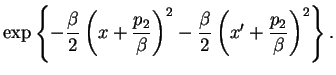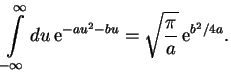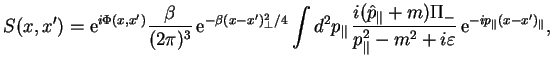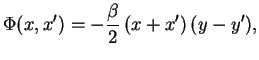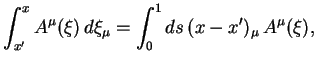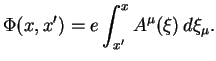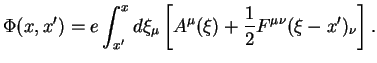Задания по квантовой теории поля

---

<< Титульный лист | Оглавление | Древесные процессы >>

Вводные задания

(Задание 1, Задание 2, Задание 3)

Задание 1. Построить базис для частицы в постоянном однородном магнитном поле.

Решение. Для любой частицы с импульсом , находящейся в электромагнитном поле, можно ввести удобный для анализа квантовых процессов с ее участием базис. Заметим, что конфигурация чисто магнитного поля, наиболее важная в приложении к астрофизическим объектам, обладает набором специфических свойств, использование которых существенно упрощает расчеты конкретных реакций.

Из электродинамики известно, что электромагнитное поле полностью определяется тензором напряженностей . В дополнение к нему также вводится дуально сопряженный тензор . Выберем систему координат таким образом, чтобы ось была направлена вдоль напряженности магнитного поля . В такой системе отсчета тензоры и имеют следующий явный вид:

В дальнейшем удобно пользоваться не самим тензором электромагнитного поля и дуальным к нему, а их безразмерными аналогами:

явный вид которых в выбранной нами системе отсчета представлен числовыми матрицами в формуле (1.1).

Представляет интерес проанализировать алгебру введенных безразмерных тензоров (1.2). Начнем с бинарных произведений:

В отличие от антисимметричных тензоров и , тензоры и симметричны в соответствии с общими свойствами сверток тензоров. В выбранной нами системе координат эти тензоры имеют следующий явный вид:

Из явного представления тензоров видно, что они не являются линейно независимыми, а связаны друг с другом посредством метрического тензора :

Проведенный анализ показывает, что наличие постоянного однородного внешнего магнитного поля естественным образом разбивает четырехмерное пространство Минковского на два непересекающихся подпространства: двумерное евклидово подпространство с метрическим тензором , ортогональное вектору напряженности магнитного поля B, и двумерное псевдоевклидово подпространство с метрическим тензором . Безразмерные тензоры электромагнитного поля и играют роль тензоров Леви-Чивита (полностью антисимметричных тензоров) этих подпространств и обладают следующими свойствами:

Для введенного набора тензоров справедливы следующие бинарные соотношения:

При конкретных вычислениях оказывается удобным ввести специальные обозначения для каждого из подпространств: - для евклидова подпространства с метрикой и - для псевдоевклидова подпространства с метрикой . При таком соглашении произвольный 4-вектор можно разбить на две ортогональные составляющие:

где и в соответствии со свойством (1.5). Такое разбиение позволяет ввести скалярное произведение векторов в каждом подпространстве по отдельности:

где и - произвольные 4-векторы.

Деление четырехмерного пространства на два непересекающихся подпространства приводит к эффективной модификации свойств -матриц. Будем обозначать -матрицы подпространства как , а подпространства - . Введем проекционные операторы :

где учтен явный вид тензора в выбранной системе отсчета. Отметим следующие мультипликативные свойства проекционных операторов:

а также их коммутационные свойства по отношению к -матрицам:

Последнее свойство интересно тем, что если встречается конструкция вида , то эффективно от -матрицы остается только ее продольная составляющая - . Следует отметить также и коммутативность проекционных операторов с матрицей :

Широко используемой операцией является взятие шпура произведения некоторого числа -матриц. В случае сильного магнитного поля вычисление шпуров эффективно реализуется только в подпространстве. Как и в обычном четырехмерном пространстве в подпространстве шпур нечетного числа -матриц равен нулю, а несколько первых шпуров четного числа - следующие:

Полезны и другие часто встречающиеся соотношения:

Легко показать, что свертка двух -матриц, между которыми находится любое нечетное число -матриц, обращается в нуль.

Наличие внешнего магнитного поля, а следовательно, и набора тензоров , , и позволяет естественным образом ввести базис четырехмерного импульсного пространства для любой частицы с 4-импульсом :

Эти векторы взаимно ортогональны, но не нормированы, поэтому приведем значения квадратов этих векторов:

Отсюда видно, что ортонормированный базис может быть легко построен как для времениподобного , так и для пространственноподобного вектора. Для безмассовой частицы на массовой поверхности () третий и четвертый базисные векторы оказываются изотропными, что не позволяет их нормировать. Однако это не мешает пользоваться набором ненормированных базисных векторов (1.17) при расчетах процессов с участием безмассовых частиц. Следует также отметить, что первый и второй базисные векторы целиком лежат в и подпространствах соответственно, в то время как третий и четвертый имеют составляющие в обоих подпространствах. Выпишем явный вид набора базисных векторов в выбранной нами системе отсчета:

Введение базиса (1.17) позволяет делать разложения 4-тензора любого ранга в соответствии с правилами:

где и - произвольные 4-вектор и 4-тензор второго ранга, а и - их составляющие в этом базисе.

Задание 2. Найти решение уравнения Дирака для фермиона с зарядом ( - элементарный заряд) в постоянном однородном внешнем магнитном поле.

Решение. Уравнение Дирака для фермиона во внешнем электромагнитном поле с 4-потенциалом  имеет вид:

где и .

Решения этого уравнения, полученные для постоянного однородного магнитного поля , получили свое наибольшее приложение в астрофизике. В частности, на поверхности пульсаров обнаружены достаточно сильние магнитные поля  Гс, а согласно теоретическим моделям в ядрах таких пульсаров напряженности полей могут быть на два-три порядка больше. В этой связи непосредственный интерес представляют не просто точные решения уравнения Дирака в магнитном поле, а их асимптотика в случае экстремально больших напряженностей.

Для решения уравнения (2.1) выберем систему координат таким образом, чтобы вектор напряженности магнитного поля B был направлен по оси , а векторный потенциал A - по оси . В такой калибровке 4-потенциал внешнего магнитного поля можно представить в виде:

Для решения поставленной задачи удобно ввести вспомогательную функцию , которая является решением квадрированного уравнения Дирака:

при этом точное решение уравнения (2.1) связано с функцией соотношением:

Найдем явный вид функции  . Используя известное свойство произведения двух -матриц - , где - метрический тензор и , а также условие Лоренца для 4-потенциала - , квадрированное уравнение (2.3) приводится к виду:

где - тензор внешнего магнитного поля, и . Можно показать, что , где - проекция релятивистского оператора спина фермиона на ось . Будем считать, что функция является собственной функцией оператора :

где собственное значение имеет смысл удвоенного среднего значения проекции спина фермиона. Тогда оператор в квадрированном уравнении (2.5) становится пропорциональным единичной матрице пространства Дирака, что позволяет фактически перейти от матричного к скалярному уравнению. Принимая во внимание явный вид 4-потенциала (2.2), распишем явно квадрированное уравнение (2.5) в выбранной нами системе координат:

где - оператор Лапласа. Оператор уравнения (2.7) не зависит явно от времени, поэтому функция является стационарным решением этого уравнения и описывает квантовую частицу с сохраняющимся значением энергии . Поскольку приведенное уравнение (2.7) имеет явную зависимость только от переменной , то оператор этого уравнения будет коммутировать с операторами и . Эти дифференциальные операторы определены в лоренцевском 4-пространстве-времени, поэтому они также будут коммутировать и с оператором , являющимся постоянной величиной в этом пространстве. Исходя из вышесказанного, будем искать положительно частотное решение уравнения (2.7) в виде:

как собственную функцию трех операторов:

с собственными значениями , и соответственно. Будем также считать, что постоянный биспинор является решением уравнения (2.6).

Подставляя решение (2.8) в уравнение (2.5) и вводя вместо  новую безразмерную переменную , получим следующее уравнение для функции :

Полученное уравнение по виду совпадает с уравнением Шредингера для одномерного гармонического осциллятора. Из нерелятивистской квантовой механики известно, что собственные функции такого уравнения обращаются в нуль при , когда собственные значения пропорциональны положительным целым нечетным числам:

где - целое неотрицательное число. Собственные функции, соответствующие этим собственным значениям, имеют вид:

где - полиномы Эрмита, а - нормировочный множитель. В итоге точные решения квадрированного уравнения Дирака и соответствующий им спектр энергии можно записать в виде:

где введены главное квантовое число , нумерующее энергетические уровни заряженного фермиона в магнитном поле (уровни Ландау) и принимающее целые неотрицательные значения, и знак заряда фермиона . Из выражения для энергии (2.14) следует, что спектр энергии фермиона имеет двукратное вырождение по квантовому числу при и бесконечнократное вырождение по числу , если оно непрерывно.

Воспользуемся уравнением (2.4), чтобы по функции восстановить функцию - точное решение уравнения Дирака в магнитном поле. Распишем явно оператор в выбранной нами системе координат и подействуем им на функцию из (2.13), что дает следующее выражение для функции :

Следует напомнить, что уравнение по переменной  (2.10) формально совпадает с уравнением Шредингера для гармонического осциллятора. Поэтому по аналогии с квантовым осциллятором удобно ввести повышающий и понижающий операторы:

Напомним действие операторов на волновую функцию осциллятора:

Если также ввести следующие линейные комбинации -матриц:

где , - матрицы Паули, то функция приводится к виду:

При таком подходе остается произвол в выборе постоянного биспинора . Зафиксируем этот произвол, потребовав, чтобы слагаемое в формуле (2.19) обратилось в нуль. Выберем биспинор вида:

который является собственной функцией оператора проекции спина , а также удовлетворяет уравнению:

Из этого уравнения следует, что слагаемое, пропорциональное повышающему оператору, обращается в нуль, если . Поэтому при таком выборе биспинора точное решение уравнения Дирака в постоянном однородном магнитном поле может быть приведено к виду:

Основным уровнем Ландау естественно считать квантовое состояние с , причем вспомогательное число , определяющее набор дискретных уровней, также равно нулю. Согласно определению энергетических уровней (2.14) на основном уровне соотношение между энергией и импульсом равно: , что соответствует свободному движению заряженного фермиона вдоль оси . При этом волновая функция заряженного фермиона оказывается связанной только с одной вспомогательной функцией соотношением:

После подстановки явного вида функции  (2.13) нормировочный множитель определяется из условия:

где интегрирование проводится по объему бесконечного (вдоль оси ) цилиндра с поперечным сечением в виде прямоугольника со сторонами и .

Отрицательно частотное решение можно получить из положительно частотного (2.23) заменами: , () и . В заключение выпишем окончательный результат для положительно и отрицательно частотных решений уравнения Дирака заряженного фермиона, находящегося на основном уровне Ландау () во внешнем постоянном однородном магнитном поле:

где , - знак заряда, - знак импульса вдоль направления магнитного поля, - постоянные спиноры, определяемые уравнением (2.20). Следует также заметить, что биспиноры нормированы условием точно так же, как положительно и отрицательно частотные решения свободного уравнения Дирака.

Задание 3. Найти пропагатор электрона в сильном магнитном поле.

Решение. Магнитное поле естественно считать сильным, если оно определяет наибольший энергетический масштаб задачи:

В этом случае электроны будут находиться на основном уровне Ландау (), что существенно упрощает задачу о нахождении пропагатора электрона в таком сильном магнитном поле.

На основном уровне Ландау электрон ( - знак заряда фермиона) имеет сохраняющуюся проекцию спина на направление, противоположное напряженности магнитного поля, ( ) и, в соответствии с (2.26), будет описываться волновой функцией вида:

где - чисто полевой параметр, и - энергия и импульс электрона, причем , - параметр с размерностью массы, определяющий положение максимума волновой функции на оси , и - длины нормировочных отрезков вдоль осей и . Для вычисления пропагатора найдем сначала матрицу плотности . Из квантовой теории поля известно, что для биспинора матрица плотности есть:

где 4-импульс и - вектор поляризации электрона в его системе покоя. Учитывая в выбранной нами системе координат корреляцию между спином электрона и направлением магнитного поля , вектор поляризации - , так что 4-вектор поляризации (3.4) сведется к . Подставляя импульс и вектор поляризации в матрицу плотности (3.3) и проводя простые алгебраические преобразования, получим следующий результат:

где - оператор проекции спина фермиона на ось . Используя определение проекционного оператора  (1.11), запишем матрицу плотности (3.5) в виде:

Для вычисления пропагатора электрона представим его волновую функцию в виде разложения по операторам рождения и уничтожения:

где в положительно и отрицательно частотных решениях (3.2) первые два индекса для краткости опущены. По определению, пропагатор электрона вычисляется как разность временного и нормального упорядочения произведения и :

Принимая во внимание свойство антикоммутации операторов рождения и уничтожения электрона, пропагатор электрона (3.8) принимает вид:

где и - временные компоненты 4-векторов и . При вычислении пропагатора электрона удобно перейти от суммирования к интегрированию:

Подставляя явный вид функций  (3.2) в пропагатор (3.9), получим:

Следует заметить, что при выводе пропагатора в случае в интеграле была сделана замена переменных и . Для проведения дальнейших преобразований воспользуемся соотношением:

Делая подстановку этого соотношения в пропагатор (3.11), получим:

Интеграл по - гауссов и берется с помощью формулы:

В результате для пропагатора электрона получается следующее:

где интегрирование ведется в подпространстве . Следует несколько слов сказать относительно фазы  . Можно показать, что она может быть получена как результат интегрирования по отрезку прямой , соединяющей точки и четырехмерного пространства-времени, так что . Вспомним также, что решение уравнения Дирака для электрона найдено нами в калибровке 4-потенциала внешнего поля вида: . Тогда интеграл, вычисленный по указанному отрезку четырехмерного пространства-времени:

с точностью до коэффициента сводится к (3.16). Поэтому фазу можно записать в следующем лоренц-инвариантном виде:

Фаза, представленная в такой форме, содержит неоднозначность, поскольку зависит от пути интегрирования. Чтобы избавиться от такой зависимости, вместо 4-потенциала введем новый 4-вектор и потребуем, чтобы он был потенциальным:

Указанного свойства можно добиться, если к потенциалу добавить 4-вектор , где - тензор внешнего постоянного электромагнитного поля. Поэтому фаза, записанная в лоренц-инвариантном виде и не зависящая от пути интегрирования, имеет вид:

В заключение отметим, что наличие этой фазы в пропагаторе электрона (3.15) делает его калибровочно и трансляционно неинвариантным.

---

<< Титульный лист | Оглавление | Древесные процессы >>

Публикации с ключевыми словами: квантовая теория поля - элементарные частицы - сверхсильные магнитные поля - рождение частиц Публикации со словами: квантовая теория поля - элементарные частицы - сверхсильные магнитные поля - рождение частиц
См. также: Бозон Хиггса: объяснение в комиксе Эволюция вселенной Лептоны Элементарные частицы Ее звали Икс Пентакварк, опять пентакварк? Протон и антипротон: похожие или одинаковые? Все публикации на ту же тему >>