Астронет > Эволюция вселенной

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Эволюция вселенной

А.Н.ВАСИЛЬЕВ

Санкт-Петербургский государственный университет

В статье кратко излагается современная теория Большого Взрыва, объясняющая эволюцию наблюдаемой Вселенной.

Картина ночного неба представляется наблюдателю некоторым эталоном стабильности по сравнению с окружающими его процессами на Земле и в обществе: на протяжении всей жизни человека видимые звезды сохраняют неизменными свои положения и яркости, сохраняется привычный рисунок созвездий, и это единообразие нарушается лишь заметным движением небольшого числа объектов типа планет или комет, относящихся к нашей Солнечной системе.

Но это первое впечатление неизменности окружающей нас Вселенной в действительности обманчиво: она эволюционирует, и эта эволюция, сравнительно медленная сейчас, на ранних этапах была невообразимо быстрой, так что серьезные качественные изменения состояния Вселенной происходили за доли секунды. По современным представлениям, наблюдаемая нами сейчас Вселенная возникла около 15 миллиардов лет назад из некоторого начального "сингулярного" состояния с бесконечно большими температурой и плотностью и с тех пор непрерывно расширяется и охлаждается. Согласно этой теории Большого Взрыва, дальнейшая эволюция зависит от измеримого экспериментально параметра $\rho$ - средней плотности вещества в современной Вселенной. Если $\rho$ меньше некоторого (известного из теории) критического значения $\rho_c$ , Вселенная будет расширяться вечно; если же $\rho$ > $\rho_c$ , то процесс расширения когда-нибудь остановится и начнется обратная фаза сжатия, возвращающая к исходному сингулярному состоянию. Современные экспериментальные данные относительно величины $\rho$ еще недостаточно надежны, чтобы сделать однозначный выбор между двумя вариантами будущего Вселенной.

Есть ряд вопросов, на которые теория Большого Взрыва ответить пока не может, однако основные ее положения обоснованы надежными экспериментальными данными, а современный уровень теоретической физики позволяет вполне достоверно описать эволюцию такой системы во времени, за исключением самого начального этапа - порядка сотой доли секунды от "начала мира". Для теории важно, что эта неопределенность на начальном этапе фактически оказывается несущественной, поскольку образующееся после прохождения данного этапа состояние Вселенной и его последующую эволюцию можно описать вполне достоверно.

Закончив на этом общее введение, переходим к более подробному изложению теории Большого Взрыва и порождаемых ею проблем. Основными экспериментальными основаниями данной теории являются следующие три:

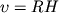Наблюдаемое "разбегание" далеких галактик, подчиняющееся закону Хаббла $\upsilon=RH$ .
Открытие в 1964 году Р. Пензиасом и А. Вильсоном космического фона "реликтового излучения", по интенсивности и спектральному составу эквивалентного излучению черного тела с температурой около 3 K (градусы Кельвина).
Наблюдаемый химический состав Вселенной, состоящей приблизительно из 3/4 (по массе) водорода и 1/4 гелия с небольшой (порядка одного процента) примесью прочих элементов.

Для описания эволюции после первой сотой доли секунды используются следующие разделы теоретической физики:

равновесная статфизика, главным образом ее основные принципы и теория релятивистского идеального газа;
общая теория относительности Эйнштейна, в частности космологическая модель Фридмана расширяющейся вселенной;
некоторые сведения из физики элементарных частиц: список основных частиц, их характеристики, типы взаимодействия, законы сохранения.

Все нужные сведения и закономерности из этих разделов являются надежно установленными, поэтому получаемую с их помощью информацию относительно эволюции системы можно считать вполне достоверной. Принципиальные трудности возникают лишь при попытке продвинуться еще ближе к "началу мира", т.е. внутрь первой сотой доли секунды. Для этого нужны надежные сведения о физике элементарных частиц в области сверхвысоких энергий, которыми мы сейчас не располагаем, поскольку такие энергии недостижимы на земных ускорителях. При дальнейшем продвижении к началу мира мы в какой-то момент столкнемся с еще более трудной проблемой необходимости "квантования гравитации", пока не имеющей даже принципиального удовлетворительного решения. В силу этих причин все попытки исследования самых первых мгновений существования нашего мира остаются пока чисто умозрительными теоретическими построениями. Поэтому мы будем просто исключать из рассмотрения это "первое мгновение" эволюции, ограничиваясь лишь последующим этапом, для которого располагаем достоверной информацией.

Прежде всего поясним подробнее перечисленные выше основные экспериментальные свидетельства в пользу теории Большого Взрыва.

1. Расширение вселенной

По данным современной наблюдательной астрономии звезды во Вселенной группируются в галактики, которые, в свою очередь, также образуют скопления. Представление о порядках величин дают следующие цифры: наша Галактика содержит ~ 10¹¹ звезд и имеет форму линзы диаметром 80 тысяч световых лет и толщиной ~ 30 тысяч световых лет. Ближайшая к нам галактика M31 в созвездии Андромеды удалена от нас на расстояние порядка 2 миллионов световых лет. Мы находимся на периферии гигантского скопления более тысячи галактик с центром в направлении созвездия Девы, удаленным на расстояние ~ 60 миллионов световых лет. Возможности современной техники позволяют наблюдать достаточно яркие галактики вплоть до расстояний порядка 10 миллиардов световых лет. Данные наблюдений показывают, что в крупных масштабах Вселенная однородна и изотропна. Грубо говоря, это означает, что в любой сфере с фиксированным достаточно большим диаметром (достаточным считается число ~ 300 миллионов световых лет) содержится приблизительно одинаковое число галактик. Утверждение об однородности и изотропности Вселенной в больших масштабах принято называть Космологическим Принципом.

В наблюдаемых спектрах звезд и галактик хорошо различимы спектральные линии поглощения (хромосферами звезд) известных элементов. Это позволяет довольно точно измерять с помощью хорошо известного эффекта Доплера скорость $\upsilon$ , с которой данный излучающий объект удаляется ( $\upsilon$ > 0) или приближается ( $\upsilon$ < 0) по отношению к земному наблюдателю. Такое движение приводит к смещению $\lambda$ \rightarrow $\lambda$ ' длины волны $\lambda$ излучающего источника:

$\frac{\lambda'}{\lambda}=\frac{1+\upsilon/c}{\sqrt{1-(\upsilon/c)^2\,}},$

(1)

где $\upsilon$ - скорость удаления, $c$ - скорость света (знаменатель (1) - поправка в релятивистской теории Эйнштейна, существенная только при $\upsilon$ , близких к скорости света $c$ ). Из (1) видно, что для удаляющегося от нас объекта линии смещаются в красную сторону ( $\lambda$ > $\lambda$ '), а для приближающегося - в голубую ( $\lambda$ < $\lambda$ ').

Если бы окружающие нас галактики двигались хаотически, то красные и голубые смещения в их спектрах наблюдались бы с одинаковой вероятностью. Но эксперимент показывает другое: красные смещения преобладают и тем больше, чем дальше от нас находятся изучаемые объекты. Количественным итогом этих наблюдений является сформулированный в 1929 году Хабблом "закон разбегания", согласно которому все галактики (в среднем) удаляются от нас и скорость этого разбегания $\upsilon$ приблизительно пропорциональна расстоянию $R$ до рассматриваемой галактики:

$\upsilon=HR, \qquad H\cong 15 \frac{\mbox{км}}{\mbox{c}} \left/ 10^6\textrm{~световых лет.}\right.$

(2)

Коэффициент пропорциональности $H$ называют постоянной Хаббла. Мы указали в (2) принимаемое сейчас большинством астрономов значение: 15 км/с на каждый миллион световых лет расстояния. Здесь следует отметить, что определение величины $H$ по данным эксперимента является очень трудной задачей: скорости $\upsilon$ по эффекту Доплера можно определить достаточно точно, но измерение расстояний $R$ до далеких галактик - труднейшая проблема, и до сих пор она решается лишь различными косвенными методами. Сам Хаббл при оценке расстояний занизил их на порядок, поэтому получил на порядок большее, чем в (2), значение $H$ (170 вместо 15). До сих пор часть астрономов считает, что значение $H$ заметно больше приведенного в (2), но большинство принимает цифру 15.

Из закона разбегания (2), разумеется, не следует, что наша галактика является центром мира, а все прочие удаляются от нее. Согласно Космологическому Принципу наша галактика ничем не выделена, так что точно такую же картину разбегания должен видеть наблюдатель из любой другой галактики. Это значит, что "все разбегаются от всех". Наглядной моделью такого разбегания может послужить надуваемый резиновый шарик с нанесенными хаотически на его поверхность точками - "галактиками": при надувании все эти точки будут удаляться друг от друга в точном соответствии с законом Хаббла (2). Это модель "двумерного замкнутого мира". Аналогичный "открытый мир" можно представить в виде резиновой плоскости с нанесенными точками, равномерно растягивающейся во всех направлениях.

Из пропорциональности $\upsilon$ и $H$ в законе (2) вытекает фундаментальный вывод относительно существования "начала мира": где-то в прошлом был момент, в который любая из наблюдаемых сейчас галактик была бесконечно близка к нашей, следовательно, "любая к любой" в силу Космологического Принципа. Из-за такого сближения плотность вещества во Вселенной в "начальный момент" становится бесконечной. Но это не означает, что все оно было собрано в одном месте, так как тот же Космологический Принцип требует, чтобы плотность становилась бесконечной в любой точке пространства.

Оценить "возраст Вселенной" $t_0$ можно очень просто, если предположить, что постоянная Хаббла $H$ в процессе расширения остается неизменной: тогда $t_0 = 1/H\cong 20$ миллиардов лет для числа из (2). На самом деле предположение о неизменности $H$ неправильно и точную оценку $t_0$ можно получить только с помощью космологической модели Фридмана (см. далее). К качественным изменениям это не приводит, а для $t_0$ тогда получается $t_0 = 2H/3\cong$ 14 миллиардов лет.

2. Реликтовое излучение

Это важнейшее космологическое открытие нашего века, которое было сделано случайно. В 1964 году астрономы Р. Пензиас и А. Вильсон решили измерить фоновое радиоизлучение нашей Галактики в направлениях вне ее плоскости эклиптики. Для этого они решили воспользоваться построенной для связи со спутниками рупорной антенной лаборатории фирмы Белл-Телефон, сконструированной так, чтобы обеспечить сверхнизкий уровень собственных шумов. Последнее очень важно, так как ожидаемое фоновое радиоизлучение галактики также подобно радиошуму, который следовало выделить на фоне других шумов от атмосферы, самой антенны и ее усилительных цепей.

После тщательного анализа и оценки всех этих "паразитных" шумов Пензиас и Вильсон начали измерения на сравнительно коротких волнах с длиной 7,35 см (микроволновый диапазон), для которых радиошум галактики должен практически отсутствовать. Они ожидали, что весь сигнал будет тогда простой суммой уже известных "паразитных шумов". Но оказалось, что кроме них система регистрирует некоторый слабый дополнительный радиошум, интенсивность которого не зависит ни от направления антенны, ни от времени суток.

Пензиас и Вильсон не понимали природы этого дополнительного радиошума и даже разобрали, почистили и вновь собрали всю антенну, чтобы исключить добавочные помехи от возможных загрязнений. Но это практически не изменило результат, и им пришлось констатировать, что по непонятным (для них) причинам их антенна принимает дополнительный слабый радиошум внеземного происхождения, интенсивность которого постоянна во времени и не зависит от направления. Измеренная ими на длине волны 7,35 см интенсивность этого радиосигнала оказалась равной интенсивности излучения на данной длине волны абсолютно черного тела с температурой около трех кельвинов. Пензиас и Вильсон наткнулись на этот факт случайно и некоторое время даже не решались опубликовать свои результаты, поскольку не понимали природы обнаруженного ими радиошума (в 1978 году они получили за свое открытие Нобелевскую премию). Но уже в конце сороковых годов появились первые работы физиков-теоретиков, в которых предсказывалось, что в настоящий момент вся Вселенная должна быть заполнена равновесным электромагнитным излучением с эффективной температурой в несколько градусов Кельвина.

Распределение по энергиям такого равновесного излучения (оно же излучение абсолютно черного тела) описывается известной формулой Планка

$d\rho=d\lambda \frac{8\pi hc}{\lambda^5}\frac{1}{e^{hc/\lambda kt}-1}\,,$

(3)

в которой $d\rho$ - энергия в единице объема, приходящаяся на интервал длин волн от $\lambda$ до $\lambda$ + $d\lambda$ , $T$ - температура в кельвинах K, $h = 6,625 \cdot10^{-27}$ эрг с - постоянная Планка, $k = 1,38 \cdot 10^{-16}$ эрг/K - постоянная Больцмана, c = 3 $\cdot 10^{10}$ см/c - скорость света.

Согласно утверждениям теоретиков, на ранней стадии Вселенная была заполнена равновесным излучением с очень высокой температурой. В процессе расширения Вселенной это излучение охлаждалось, оставаясь равновесным, и к настоящему времени температура опустилась до значений нескольких градусов Кельвина. Именно это "реликтовое излучение", оставшееся от начальной фазы горячей ранней Вселенной, обнаружили Пензиас и Вильсон. Они узнали об этом, вступив в контакт с физиками из Принстонского университета, которые были знакомы с теорией горячей (на ранней стадии) Вселенной и уже строили специальную антенну для обнаружения реликтового излучения. Но Пензиас и Вильсон их опередили.

Наличие реликтового излучения считается в настоящий момент достоверно установленным фактом. Основной проверкой является возможность его измерения на разных длинах волн $\lambda$ : интенсивность сигнала должна быть пропорциональной известной из (3) величине $d\rho/d\lambda$ с одной и той же для всех $\lambda$ температурой $T$ . В настоящее время измерения выполнены для десятков различных длин волн как в микроволновой, так и в инфракрасной области спектра электромагнитных волн (согласно распределению (3) максимум интенсивности при $T$ = 3 K соответствует $\lambda$ = 0,1 см, более короткие волны относятся уже к инфракрасной области). По последним данным, полученным с помощью установленной на спутниках аппаратуры, современное значение температуры реликтового излучения есть 2,74 K. Точность этих измерений уже настолько высока, что она позволила обнаружить наличие слабой анизотропии реликтового излучения, объясняющейся движением земного наблюдателя через заполненное излучением пространство. Вследствие того же эффекта Доплера излучение прямо по направлению движения должно казаться немного более горячим, а в обратном направлении - более холодным. Эти небольшие (порядка 10^-3 от основной величины) вариации температуры были обнаружены экспериментально, и они имеют характерную ( $\propto\cos\theta$ ) угловую зависимость. По этим данным можно вычислить скорость движения Земли относительно этого "нового эфира", образованного фоном реликтового излучения. В итоге получается значение порядка 600 км/с. Помимо этой "кажущейся" анизотропии, в экспериментах обнаружена и настоящая (не связанная с движением Земли) анизотропия реликтового излучения. Она очень мала (порядка 10^-5 от основной величины), поэтому с высокой степенью точности реликтовое излучение можно считать однородным и изотропным. Но сам факт наличия хотя бы очень слабой анизотропии принципиально важен для различных теорий, пытающихся объяснить и описать математически происхождение галактик.

3. СОСТАВ ВСЕЛЕННОЙ

Как уже было сказано, по данным наблюдений Вселенная состоит в основном из водорода (3/4 по массе) и гелия (1/4), прочие элементы составляют примесь порядка одного процента. Эти данные получены по спектрам звезд и межзвездного газа и хорошо согласуются с теоретическими моделями астрофизики, описывающими состав и эволюцию звезд. Приведенные выше цифры 3/4 и 1/4 относятся к начальной фазе этой эволюции, в процессе которой в звездах вырабатываются и другие, в том числе тяжелые, элементы.

По современным представлениям, где-то в первые минуты своего существования Вселенная прошла "эру нуклеосинтеза" (подробнее потом), во время которой и образовались водород и гелий в пропорции 3 : 1 плюс ничтожная примесь других легких элементов, в частности лития Li, и изотопов водорода - дейтерия D и трития T. Все прочие более тяжелые элементы образовались уже гораздо позднее внутри звезд, а в межзвездное пространство они попадают при взрывах сверхновых и т.п. Как это ни странно, именно простой факт преобладания водорода во Вселенной позволил теоретикам предсказать необходимость существования реликтового излучения.

Для дальнейшего изложения также важно сопоставить плотность ядерных частиц (протонов и нейтронов) в наблюдаемой Вселенной с плотностью числа фотонов в реликтовом излучении. Согласно теории Планка, равновесное электромагнитное излучение можно рассматривать как некоторый идеальный газ безмассовых частиц - фотонов, имеющих энергию $\overline{E}=hc/\lambda=h\nu$ для длины волны $\lambda$ . Плотность энергии (3) связана с плотностью числа фотонов $n$ очевидным соотношением $d\rho = dn \cdot E_{\lambda}$ , так что из (3) определяется и распределение числа фотонов по длинам волн. Интегрируя $dn$ по всем $\lambda$ , получим полное число фотонов $n$ в единице объема, аналогичный интеграл от $d\rho$ из (3) дает объемную плотность энергии $\rho$ , частное $\rho/n$ - среднюю энергию одного фотона $\overline E$ . Все эти величины зависят только от температуры $T$ и мировых констант:

$\rho = a_{1}T^{4}~$ [эрг/см³], $n = a_{2}T^3$ [фотонов/см³],

$\rho = a_{1}T^{4}~$ [эрг/см³], $n = a_{2}T^3$ [фотонов/см³], (4)

$\overline E = a_{3}T~$ [эрг],

где $T$ - температура в кельвинах, $a_i$ - известные константы: $a_{1} = 7,56\cdot 10^{-15}, a_{2} = 20,28, a_{3} = 3,73\cdot 10^{-16}$ . Первое из соотношений (4) называется законом Стефана-Больцмана. Из (4) следует , что при современной температуре $T$ = 3 K в фоне реликтового излучения содержится 550 миллионов фотонов на 1 кубометр. Оценка плотности вещества по данным наблюдений остается пока неопределенной, но в любом случае не выходит из границ от 6 до 0,03 ядерных частицы на 1 кубометр (критической плотности соответствует число 3). Таким образом, на одну ядерную частицу приходится порядка 10⁸ - 10¹⁰ фотонов. В дальнейшем при оценках будем принимать цифру 10⁹ : один миллиард фотонов на одну ядерную частицу.

Хотя это очень большое число, основная энергия сейчас сосредоточена в веществе, а не в излучении. Энергия $E = mc^2$ одной ядерной частицы равна приблизительно 1000 МэВ (МэВ = 1 миллион электронвольт), тогда как получаемая из (4) средняя энергия одного фотона при $T$ = 3 K составляет в тех же единицах (1 эрг = $6,24\cdot10^{11}$ эВ) приблизительно $7\cdot10^{-4}$ эВ. Эта величина даже после умножения на 10⁹ остается на три порядка меньше энергии одной ядерной частицы, так что подавляющая доля плотности энергии приходится сейчас на вещество. Но так было не всегда: на ранней стадии основная доля энергии приходилась на излучение (см. ниже).

Переходя к описанию самого процесса эволюции, выделим мысленно в пространстве произвольную сферу достаточно большого радиуса $R$ ("достаточно" для справедливости Космологического Принципа) и будем следить за эволюцией во времени содержащегося внутри данной области излучения и вещества, предполагая их распределение однородным и изотропным. Термин "излучение внутри данной сферы", конечно, условен, поскольку фотоны могут выходить из нее и приходить извне. Но эти два процесса в силу предполагаемой однородности взаимно компенсируют друг друга, так что понятие "количество излучения (энергии) внутри данной сферы" имеет смысл. Согласно закону Хаббла (1) радиус рассматриваемой области растет со скоростью $\upsilon =\dot R = HR$ . Поскольку количество вещества внутри сферы остается неизменным, его плотность изменяется по закону $\rho_\textrm{\normalsize вещ}\propto R^{-3}$ . Это относится и к энергетической, и к массовой плотности, так как они связаны простой пропорциональностью $E = mc^2$ .

Рассмотрим теперь энергию реликтового излучения. В настоящий момент Вселенная практически прозрачна для электромагнитных волн (раз мы видим далекие галактики), т.е. сейчас излучение фактически не взаимодействует с веществом и эволюционирует самостоятельно. Его можно рассматривать как релятивистский газ фотонов с некоторой температурой $T$ , находящийся внутри сферы радиуса $R$ и адиабатически (т.е. без обмена теплом с внешней областью) расширяющийся. Из статистической физики известно, что полная энтропия такого газа пропорциональна $VT^{3} (V = 4\pi R^{3}/3$ - объем сферы) и остается постоянной в процессе расширения. Отсюда следует, что $R$ и $T$ связаны соотношением $RT$ = const, т.е. $T\propto 1/R$ . Это значит, что в тот момент прошлого, когда все галактики были вдвое ближе друг к другу, Вселенная была вдвое горячее и что "очень давно" она была "очень горячей". Термин "температура Вселенной" в данной фазе обозначает температуру реликтового излучения и не имеет отношения к веществу.

Из сказанного выше и первого равенства (4) следует, что энергетические плотности вещества и излучения связаны с $R$ и $T$ следующими соотношениями: $\rho$ _изл $\propto T^4$ , $\rho$ _вещ $\propto T^3$ , $T\propto 1/R$ . Из них следует, что при "движении в прошлое" ( $R\rightarrow 0, T\rightarrow \infty$ ) величина $\rho$ _изл растет быстрее, чем $\rho$ _вещ . Поэтому современная "эпоха вещества" ( $\rho$ _изл $\ll\rho$ _вещ) где-то в прошлом обязательно должна переходить в "эпоху излучения" ( $\rho$ _изл $\gg\rho$ _вещ) с другой зависимостью $\rho$ от $R$ и $T$ .

Рассмотрим в общих чертах основные этапы эволюции, двигаясь назад по направлению к "началу мира" и принимая за независимую переменную температуру $T$ (впоследствии мы увяжем ее с возрастом Вселенной). С ростом $T$ растет средняя энергия фотона (4), по порядку величины равная $kT$ . Качественные изменения происходят тогда, когда величина $kT$ достигает значений порядка энергии связи электронов в атомах и молекулах (~ 1 эВ), затем ядер (~ 1 МэВ), затем - порогов рождения пар частица - античастица, сначала для самых легких элементарных частиц, потом с ростом $T$ - все более тяжелых. Поясним подробнее. Элементарные частицы характеризуются своей массой покоя $m$ (обычно вместо $m$ приводится значение соответствующей энергии $E = mc^2$ в электронвольтах), а также дискретными квантовыми числами: спином (внутренний момент количества движения) и различными зарядами - электрическим, барионным и лептонным. В подходящих единицах спин любой частицы является целым или полуцелым числом, частицы с целым спином являются бозонами, с полуцелым - фермионами. Фотон - частный случай бозона со спином 1 и нулевыми значениями $m$ и всех трех зарядов. Если для данного сорта частиц $kT\gg mcE^2$ , то их массой можно пренебречь, и тогда для любых бозонных частиц распределение по энергиям будет иметь тот же вид (3), что и для фотонов, а для фермионов знак минус в знаменателе (3) заменится знаком плюс. Это приведет лишь к незначительному (множители типа 7/8) изменению коэффициентов в формулах (4), так что различие между бозонами и фермионами $kT\gg mcE^2$ несущественно.

Большинство частиц имеет соответствующую пару - античастицу с той же массой и спином и противоположными значениями всех зарядов. Все три заряда сохраняются в любых процессах взаимодействия элементарных частиц. При их столкновениях могут происходить любые взаимопревращения частиц, допустимые по энергии и законам сохранения зарядов. В частности, при столкновении двух фотонов с достаточно высокой энергией могут рождаться различные пары частица - античастица. Такие процессы начинаются, когда величина $kT$ достигает порогового значения $mc^2$ для данного сорта частиц, и становятся весьма интенсивными при $kT\gg mcE^2$ . Перечислим наиболее важные элементарные частицы, указывая в скобках их традиционные обозначения, энергию покоя $E = mc^2$ и порядок величины пороговой температуры: электрон и его античастица позитрон ( $e^\pm$ , $E$ = 0,5 МэВ, $T = 6 \cdot 10^9$ K), аналогичные пары мю-мезонов ( $\mu^\pm$ , $E = 10^6$ МэВ), пи-мезонов ( $\pi^\pm$ , $\pi^{0}$ , E ~ 135 МэВ) с пороговой температурой порядка 10¹² K, наконец, ядерные частицы протон (пара $p$ , $\overline{p}$ , $E$ = 938,26 МэВ) и нейтрон (пара $n$ , $\overline{n}$ , $T$ = 939,55 МэВ) с пороговой температурой 10¹³ K. Нейтрон немного (на 1,3 МэВ) тяжелее протона, и это важно для эры нуклеосинтеза.

Теперь мы можем проследить эволюцию "назад по времени" при нарастании температуры $T$ . Первое качественное изменение происходит при $T$ ~ 3000 K, когда $kT$ достигает величин порядка 1 эВ и излучение начинает разбивать атомы. Вещество тогда превращается в плазму, состоящую из свободных ядер и электронов, ее плотность нарастает ~ $T^3$ при дальнейшем росте $T$ . Через какое-то время при $T$ порядка 10⁴ K такая среда становится уже непрозрачной для излучения: фотоны рассеиваются на свободных электронах и ядрах, и это приводит к установлению общего теплового равновесия между излучением и веществом с общей для всей системы температурой $T$ . Следующий важный этап - $T$ ~ 10¹⁰ K, когда начинается интенсивное рождение электрон-позитронных пар (порог $6 \cdot 10^9$ K) и процессы развала ядер на их составляющие - свободные нейтроны и протоны. Плотность массы в этот период достигает значений порядка 10⁵ г/см³. Столь высокая плотность увеличивает число взаимных столкновений, и это обеспечивает установление термодинамического равновесия для всех типов присутствующих в системе частиц. До порога рождения пар $p$ , $\overline{p}$ и $n$ , $\overline{n}$ еще далеко ( $T$ _пор ~ 10¹³ K), поэтому отношение числа протонов $N_p$ к числу нейтронов $N_n$ определяется классической формулой Гиббса

$N_{p}/N_{n}=\exp\left\{(m_{n}-m_{p})c^{2}/kT\right\} =\exp\left\{1,3 \textrm{МэВ}/kt\right\}\,,$

(5)

что при $T = 10^{10}$ K дает $N_p / N_n \cong 76/24$ .

Если бы процесс нуклеосинтеза происходил именно в этот момент, то практически все нейтроны должны были бы войти в состав наиболее устойчивых ядер ⁴He (два нейтрона плюс два протона), что привело бы к результату $M_{H} / M_{He}$ = 52/48 для отношения масс водорода и гелия. Экспериментальное значение этого отношения другое, а именно 3 : 1. Это доказывает, что процесс нуклеосинтеза реально происходит позднее при более низких температурах, когда определяемый соотношением (5) баланс еще больше смещается в пользу протонов. Например, при $T = 10^9$ K из (5) получим $N_{p} / N_{n}$ = 86/14, откуда $M_{H}/M_{He}$ = 72/28, что уже согласуется с экспериментом.

Для объяснения такой задержки нуклеосинтеза как раз и требуется наличие очень большого числа фотонов на одну ядерную частицу. Это число не определяется автоматически условиями термодинамического равновесия. Оно остается неизменным на протяжении рассматриваемого периода эволюции, поскольку обе плотности числа частиц изменяются по одному и тому же закону ~ $T^{3} ~ 1/R^{3}$ (т.е. полное число частиц сохраняется). Если бы фотонов (излучения) не было, то при $T$ = 10¹⁰ K протоны и нейтроны уже могли бы сливаться в ядра ⁴He, так как их энергия связи превышает характерную тепловую энергию $kT\cong$ 1 МэВ. Наличие фотонов с такой же энергией тормозит процесс нуклеосинтеза, поскольку фотоны, сталкиваясь с ядрами, способствуют их развалу на исходные элементы. Этот конкурирующий с нуклеосинтезом процесс идет тем быстрее, чем больше плотность числа фотонов. Для обеспечения задержки нуклеосинтеза вплоть до температур порядка 10⁹ K (что нужно для объяснения экспериментального отношения 3 : 1), согласно расчетам специалистов по ядерным реакциям, необходима очень высокая плотность числа фотонов порядка 10⁸ - 10¹⁰ на ядерную частицу. Она столь велика, что даже к настоящему времени должна оставить заметный след в форме реликтового излучения - именно из этих соображений оно и было предсказано теоретиками.

При дальнейшем росте $T$ начнутся процессы рождения пар более тяжелых частиц. Вещество Вселенной будет тогда представлять собой некоторый очень горячий и очень плотный "суп" из всех допустимых по энергиям частиц и античастиц, находящийся в состоянии теплового равновесия. В какой-то момент энергии станут столь высоки, что мы войдем в ту область физики элементарных частиц, о которой мало что пока знаем. Наконец, при "планковских энергиях", соответствующих $T$ ~ 10³² K , гравитационное взаимодействие по силе сравняется с прочими (сильными, слабыми, электромагнитными), и его уже нельзя будет рассматривать чисто классически: возникает проблема квантования гравитации. Но важно, что все эти неопределенности относятся только к начальному этапу, а после охлаждения до температуры порядка 10¹¹ K все становится уже вполне предсказуемым.

Нам еще хотелось бы связать шкалу температур со временем - возрастом Вселенной. Для этого нужны уравнения Фридмана для расширяющейся однородной и изоторопной Вселенной. Их вывод сложен, так как опирается на общую теорию относительности Эйнштейна. Но конечный результат прост и может быть сформулирован в виде дифференциального уравнения

${\dot R}^{2}-\frac{8\pi GR^{2}\rho}{3} = \mbox{~const}$

(6)

в котором $R$ - радиус рассматриваемой сферы, $\dot R=\upsilon$ - скорость ее расширения, $\rho$ - полная массовая плотность (вещества плюс излучения) Вселенной, $G = 6,67\cdot10^{- 8}$ см³/(г с) - гравитационная постоянная. Для вещества $\rho\approx R^{- 3}$ , а для излучения $\rho\approx R^{- 4}$ , поэтому на ранней стадии эволюции ( $R\rightarrow$ 0) слагаемое с $\rho$ в (6) важнее константы в правой части, и последней можно пренебречь. Тогда уравнение (6) легко решается: для эпохи излучения ( $\rho$ = const $\cdot R^{-4}$ ) получим $R\approx t^{1/2}$ , а для эпохи вещества ( $\rho$ = const $\cdot R^{-3}$ ) получим $R\approx t^{2/3}$ . При учете связи $R\approx 1/T$ тогда имеем $t\approx T^{-2}$ в первом случае и $t\approx T^{-3/2}$ во втором. Это позволяет связать шкалу температур со шкалой времени, причем для температур выше 10⁴ K следует пользоваться соотношениями эпохи излучения, а для более низких температур - эпохи вещества.

Элементарный расчет тогда показывает, что "планковская температура" $T$ = 10³² K достигается через 10^{- 43} секунд от начала мира, $T$ = 10¹³ K - через 10^{- 6} секунд, $T$ = 10¹⁰ K - через 1 секунду, $T$ = 10⁹ K - через 1 минуту, $T$ = 10⁴ K (смена эпох) - через 100 тысяч лет, $T$ = 10³ K - через 1 миллион лет. Таким образом, первичный нуклеосинтез завершается уже через несколько минут от "начала мира", а формирование атомов - через миллион лет. После этой довольно бурной стадии начальный этап эволюции завершается и переходит в рутинный процесс расширения, который мы и наблюдаем сейчас, спустя приблизительно 15 миллиардов лет от "начала мира".

Приведенное здесь изложение теории Большого Взрыва было по необходимости кратким и неполным. Более подробную информацию можно найти в книгах [1],[2].

Информацию о более поздних и пока что дискуссионных исследованиях в данной области (ранняя Вселенная, происхождение асимметрии частица-античастица и др.) можно найти в статьях [3],[4] (за указание этих ссылок автор признателен рецензенту А.М. Черепащуку), а также в книгах [5],[6].

Литература


[1].	Вайнберг С. Первые три минуты. М.: Энергоиздат, 1981.
[2].	Силк Дж. Большой взрыв. М.: Мир, 1982.
[3].	Долгов А.Д., Зельдович Я.Б. Вещество и антивещество во Вселенной // Природа. 1982. No 8. С. 33 - 45.
[4].	Зельдович Я.Б. Современная космология// Природа. 1983. No 9. С. 11 - 24.
[5].	Линде А.Д. Физика элементарных частиц и инфляционная космология. М.: Наука, 1990.
[6].	Долгов А.Д., Зельдович Я.Б., Сажин М.В. Космология ранней Вселенной. М.: Изд-во МГУ, 1988.

Публикации с ключевыми словами: элементарные частицы - разбегание галактик - эволюция Вселенной - первичный нуклеосинтез - Реликтовое излучение - Космология
Публикации со словами: элементарные частицы - разбегание галактик - эволюция Вселенной - первичный нуклеосинтез - Реликтовое излучение - Космология

См. также:

Диполь реликтового излучения: полет сквозь Вселенную

Разложение далекого света

Карта реликтового излучения от "Планка"

Формирование галактик в магнитной Вселенной

Газ в скоплении галактик создает дыру в реликтовом излучении

"Эффекты" Зельдовича, запечатлённые на нашем небе

Сверхновая 1994D и неожиданная Вселенная

Все публикации на ту же тему >>

Мнения читателей [8]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

$\rho = a_{1}T^{4}~$ [эрг/см³], $n = a_{2}T^3$ [фотонов/см³],	(4)
$\overline E = a_{3}T~$ [эрг],