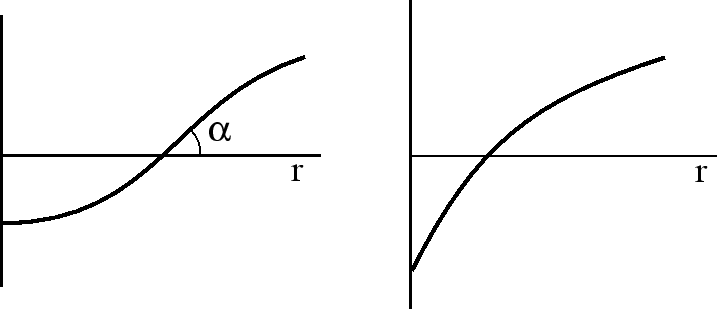<< 9.2 Движение частиц в ... | Оглавление | 9.4 Общие свойства равновесия ... >>
9.3 Сферически-симметричное поле внутри звезды
Займемся теперь уравнениями в веществе. Начнем с уравнения
(3) из раздела 9.1. Оно содержит
только ![]() . Пусть задано
. Пусть задано ![]() .
.
Известный метод решения неоднородных уравнений -- метод вариации констант. Мы знаем, что
![]() удовлетворяет однородному уравнению. Будем теперь считать, что
удовлетворяет однородному уравнению. Будем теперь считать, что ![]() не
является константой. Тогда после подстановки
не
является константой. Тогда после подстановки ![]() в неоднородное уравнение все члены, не содержащие
в неоднородное уравнение все члены, не содержащие
![]() , сократятся, а мы получим
, сократятся, а мы получим
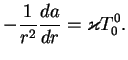
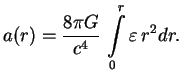
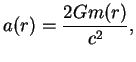
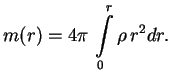
Результат получился вроде бы тривиальный. Но на самом деле это не так. Элемент объема
вовсе не равен
![]() . Поскольку метрика неевклидова, расстояние между равно не
. Поскольку метрика неевклидова, расстояние между равно не
![]() , а
, а
![]() , т. е.
, т. е.
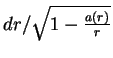 , так что
, так что
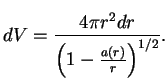
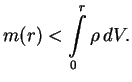
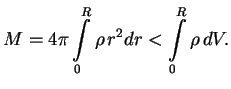
Если отдельные куски вещества (так же сжатые, как в звезде) разнести далеко друг от друга, то их полная масса была бы равна
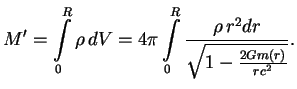
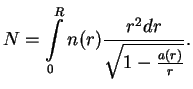
![]() -- это минимальная энергия, необходимая для того, чтобы ``распылить''
звезду на бесконечность.
-- это минимальная энергия, необходимая для того, чтобы ``распылить''
звезду на бесконечность.
Плотность вещества
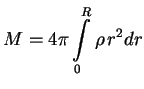
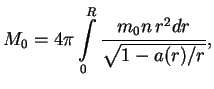
Поэтому в принципе энергия связи звезды
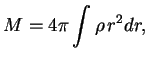
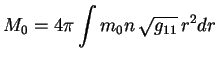
Запишем выражение для массы звезды в виде
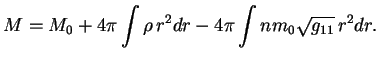
Введем
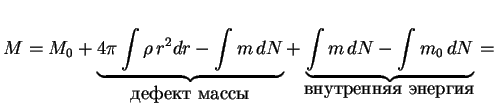
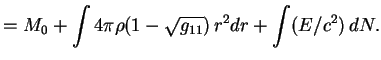
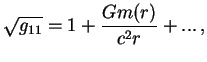
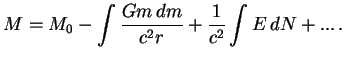
Полученное соотношение было точным выражением для полной энергии звезды в ньютоновской теории. По порядку величины
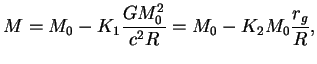
В следующем порядке появляется член
![]() . Мы уже знаем, что при
. Мы уже знаем, что при
![]() , т.е.
член
, т.е.
член ![]() исчезает, и для расчета устойчивости становятся важны поправки
исчезает, и для расчета устойчивости становятся важны поправки
![]() . Эффекты ОТО приводят к тому, что при центральной плотности звезды
больше некоторой, массы белых карликов начинают убывать
(см. рис. 45). Важен также учет ОТО
для случая сверхмассивных горячих звезд, где из-за роли давления излучения показатель
адиабаты также стремится к 4/3.
. Эффекты ОТО приводят к тому, что при центральной плотности звезды
больше некоторой, массы белых карликов начинают убывать
(см. рис. 45). Важен также учет ОТО
для случая сверхмассивных горячих звезд, где из-за роли давления излучения показатель
адиабаты также стремится к 4/3.
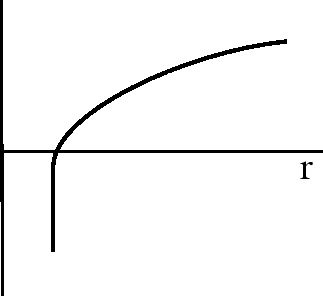
Не решая пока уравнения Эйнштейна до конца, попробуем уже сейчас выяснить некоторые свойства метрики внутри звезды. Из-за сферической симметрии достаточно рассмотреть геометрию одной ``плоскости'', проходящей через центр, чтобы охарактеризовать все трехмерие. Метрика такой поверхности такая же, как в плоском трехмерном пространстве на изогнутой поверхности вращения (``тарелке'', см. рис. 55a). Для такой поверхности
![$\displaystyle g_{11}=\left[1-{2Gm(r)\over{rc^2}}\right]^{-1},
$](https://images.astronet.ru/pubd/2008/02/15/0001226214/img1875.gif)
т.е. в центре появляется коническая точка с бесконечной кривизной
(рис. 55b) --
это решение является асимптотической серии несингулярных решений при
![]() .
.
Рассмотрим теперь асимптотику при
![]() ,
,
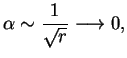
Продолжим решение уравнений. До сих пор мы использовали только одно уравнение ОТО, куда входит
слева ![]() (и не входит
(и не входит ![]() ), а в правую часть
), а в правую часть
![]() .
.
Очень важно заметить, что до сих пор не подразумевалось, что распределение плотности равновесно.
Необходим только покой (
![]() ). Скорости равны нулю, а ускорения могут быть
любыми. Условие равновесия мы нигде не использовали. Поэтому полученное выражение для
). Скорости равны нулю, а ускорения могут быть
любыми. Условие равновесия мы нигде не использовали. Поэтому полученное выражение для ![]() удобно в дальнейшем использовать для исследования устойчивости звезды.
удобно в дальнейшем использовать для исследования устойчивости звезды.
Вернемся к равновесным звездам. Следующие уравнения (вместе с условиями стационарности
![]() ), куда входит давление, дадут условие равновесия. Ограничимся случаем
паскалевой жидкости
), куда входит давление, дадут условие равновесия. Ограничимся случаем
паскалевой жидкости
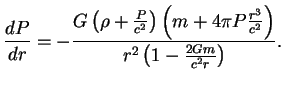
Напомним, что в ньютоновской теории
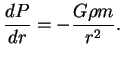
Надо иметь ввиду, что физический градиент давления равен
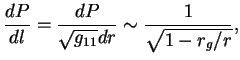
Задавшись уравнением состояния ![]() , можно интегрировать уравнение равновесия и
уравнение непрерывности
, можно интегрировать уравнение равновесия и
уравнение непрерывности
Что будет, если центральная плотность очень велика (
![]() ),
не получится ли бесконечная масса? Возьмем степенное уравнение состояния. Пусть
),
не получится ли бесконечная масса? Возьмем степенное уравнение состояния. Пусть
![]() -- плотность барионов,
-- плотность барионов, ![]() -- энергия на барион. В изэнтропическом случае
-- энергия на барион. В изэнтропическом случае
![]() . Поскольку
. Поскольку
![]() ,
,
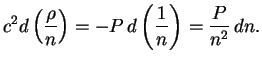
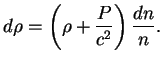
Пусть
![]() ,
,
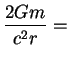 const
const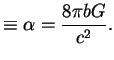
Подставляя ![]() и
и ![]() в уравнение равновесия, получим
в уравнение равновесия, получим
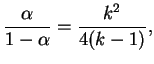
Текущая масса ![]() , но это справедливо только в области больших плотностей,
затем
, но это справедливо только в области больших плотностей,
затем ![]() спадает быстрее, чем
спадает быстрее, чем ![]() , и
, и ![]() становится конечным. Таким образом,
даже при
становится конечным. Таким образом,
даже при
![]() масса остается конечной! При этом общая масса
звезды зависит от того значения плотности
масса остается конечной! При этом общая масса
звезды зависит от того значения плотности ![]() , при котором уравнение состояния
перестает быть степенным, т. е. где нарушается пропорциональность
, при котором уравнение состояния
перестает быть степенным, т. е. где нарушается пропорциональность ![]() и
и ![]() .
.
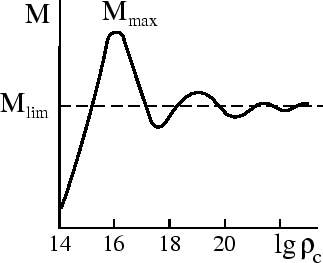
Аналитическое исследование для степенных уравнений состояния и численные расчеты
показывают, что зависимость ![]() ведет себя как на
рис. 57, т. е. после
первого максимума возникают колебания кривой
ведет себя как на
рис. 57, т. е. после
первого максимума возникают колебания кривой ![]() . Анализ показывает, что
все решения за первым максимумом неустойчивы. Значение максимальной массы
. Анализ показывает, что
все решения за первым максимумом неустойчивы. Значение максимальной массы ![]() получается разным при разных уравнениях состояния. Для газа свободных нейтронов
Оппенгеймер и Волков получили
получается разным при разных уравнениях состояния. Для газа свободных нейтронов
Оппенгеймер и Волков получили
![]() 9.3. Современные
расчеты, учитывающие межнуклонные взаимодействия, дают для нейтронных звезд
9.3. Современные
расчеты, учитывающие межнуклонные взаимодействия, дают для нейтронных звезд
![]() . Еще раз напомним, что масса здесь понимается как источник
гравитационного поля для внешнего наблюдателя. Масса того же числа барионов существенно
больше
. Еще раз напомним, что масса здесь понимается как источник
гравитационного поля для внешнего наблюдателя. Масса того же числа барионов существенно
больше
![]() , так что энергия связи
отрицательная. Нейтронные звезды большой массы устойчивы относительно разлета на
бесконечность, при их образовании выделяется энергия
, так что энергия связи
отрицательная. Нейтронные звезды большой массы устойчивы относительно разлета на
бесконечность, при их образовании выделяется энергия ![]() начальной энергии покоя,
т.е. величина, во много раз превышающая ядерную энергию.
начальной энергии покоя,
т.е. величина, во много раз превышающая ядерную энергию.
Задача. Известно, что при предельно жестком уравнении состояния
![]() const
const![]() (Я.Б.Зельдович) в ньютоновской теории масса звезды
(Я.Б.Зельдович) в ньютоновской теории масса звезды
![]() при
при
![]() . С помощью уравнения гидростатики показать, что
в ОТО даже в случае несжимаемой жидкости (
. С помощью уравнения гидростатики показать, что
в ОТО даже в случае несжимаемой жидкости (
![]() const)
масса остается конечной при
const)
масса остается конечной при
![]() .
.
<< 9.2 Движение частиц в ... | Оглавление | 9.4 Общие свойства равновесия ... >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |