Астронет > 8.4 Гравитационное красное смещение. Замедление времени

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Физические основы строения и эволюции звезд

<< 8.3 Физика искривленного ... | Оглавление | 9. Сильные гравитационные поля ... >>

8.4 Гравитационное красное смещение. Замедление времени

В предыдущих разделах мы увидели, что основная идея ОТО о движении тел в искривленном пространстве-времени по геодезическим означает, что все тела падают в гравитационном поле по одинаковым траекториям с одинаковым ускорением.

Рис. 53.

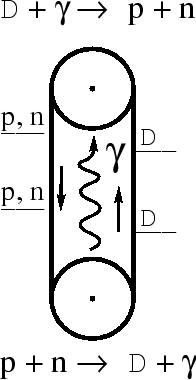
Покажем сейчас с помощью ОТО и квантовой механики, что в гравитационном поле происходит замедление времени. Для этого рассмотрим один проект вечного двигателя. На установке из двух блоков (рис. 53) будем поднимать ядра дейтерия, а опускать протоны и нейтроны.

Пусть внизу протоны реагируют с нейтронами, а образующиеся $\gamma$ -кванты используются наверху для диссоциации дейтерия. Масса на 2,2 МэВ меньше , поэтому под действием большей тяжести p-n система будет отдавать энергию, совершать вечное движение.

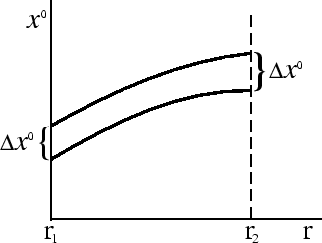
Ошибка этого проекта в том, что в действительности $\gamma$ -квант не поглотится, так как часть его энергии уйдет на преодоление силы тяжести:

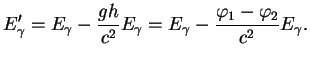
$\displaystyle E'_{\gamma}=E_{\gamma}-{gh\over{c^2}}E_{\gamma}=E_{\gamma}-{\varphi_1-\varphi_2\over{c^2}} E_{\gamma}. %% izmenil znak! \varphi$

Энергия $\gamma$ -кванта $E_\gamma=\hbar \omega$ . Поскольку $E'_{\gamma}<E_{\gamma}$ , то $\omega'<\omega$ , т. е. частота фотонов испытывает красное смещение в гравитационном поле. Этот эффект уже наблюдался на Земле с помощью эффекта Мессбауэра (опыт Паунда и Ребки).

В общем случае можно написать

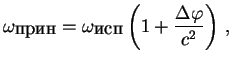
$\displaystyle \omega_{\mbox{прин}}=\omega_{\mbox{исп}}\left(1+\frac{\Delta\varphi}{c^2}\right)\,,$

где $\Delta\varphi$ -- различие гравитационного потенциала в местах испускания и приема. Это соотношение верно для фотонов любых частот. В данном месте частота фотонов зависит только от свойств испускающих их атомов (или ядер). На этих же свойствах основано и измерение времени в данном месте (атомные часы). Поэтому наблюдатель, находящийся в точке с другим гравитационным потенциалом, будет интерпретировать сдвиг частот как изменение хода времени:

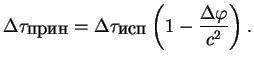$\displaystyle \Delta\tau_{\mbox{прин}}=\Delta\tau_{\mbox{исп}}\left(1-{\Delta\varphi\over{c^2}}\right).$

(8.2)

Рис. 54.

Раньше мы говорили об изменении в гравитационном поле метрики вообще, а теперь видим более конкретно, что изменяется течение времени в разных точках. Это можно интерпретировать как изменение коэффициента $g_{00}$ при временной координате в метрике. Рассмотрев как изменяется $g_{00}$ в слабом поле (т. е. ньютоновском случае), мы увидим, что $g_{00}$ играет роль ньютоновского потенциала для медленных частиц.

Рассмотрим статическое гравитационное поле. По определению это значит, что метрику можно написать в виде

$\displaystyle ds^2=g_{00}(dx^0)^2+g_{\alpha\beta}\,dx^{\alpha}dx^{\beta}\qquad (\alpha,\beta=1,2,3),$

причем ни $g_{00}$ , ни $g_{0\alpha}$ не зависят от временной координаты

. Пусть в некоторой точке

испускаются два световых сигнала с запаздыванием $\Delta x^0$ и принимаются в точке

(см. рис. 54). Поскольку $g_{ik}$ от

не зависит, мировая линия второго сигнала отличается от первой только сдвигом по координате

на $\Delta x^0$ , т. е. запаздывание сигналов в точке приема по координатному времени тоже будет $\Delta x^0$ . Однако наблюдатель пользуется не координатным, а собственным временем $\tau$ . Это соответствует тому, что он в своей окрестности пользуется метрикой

$\displaystyle ds^2=c^2d\tau^2-dl^2.$

Интервал между двумя событиями -- приходом сигналов в точку

-- инвариантен (не зависит от выбора метрики), т. е.

$\displaystyle \sqrt{g_{00}(2)\,}\,\Delta x^0=c\;\Delta\tau_2.$

Отсюда и из (8.2) получаем связь $g_{00}$ и ньютоновского потенциала $\varphi$ :

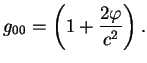
$\displaystyle g_{00}=\left(1+{2\varphi\over{c^2}}\right).$

<< 8.3 Физика искривленного ... | Оглавление | 9. Сильные гравитационные поля ... >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы

См. также:

Переработка вещества в Кассиопее А

NGC 7789: Роза Каролины

Планетарная туманность NGC 2818 от Хаббла

Научная конференция "Наблюдаемые проявления эволюции звезд" в САО РАН

Планетарные туманности

Прошлые и будущие звёзды Андромеды

Туманность Ожерелье

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце