Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Физические основы строения и эволюции звезд
<< 8.2 Параллельный перенос векторов | Оглавление | 8.4 Гравитационное красное смещение... >>

8.3 Физика искривленного пространства-времени

В отсутствие гравитационного поля физика разворачивается в псевдоевклидовом пространстве Минковского с метрикой

$\displaystyle ds^2=c^2dt^2-dx^2-dy^2-dz^2. $

При наличии гравитации, т. е. в ОТО, будем считать, что пространство искривлено:

$\displaystyle ds^2=g_{ik}(x)\,dx^idx^k,\;\;g_{ik}=g_{ki}$ (8.1)

(по повторяющимся индексам предполагается суммирование).

Если задан метрический тензор $ g_{ik}$ (для краткости будем говорить ``метрика'' $ g_{ik}$),то можно найти геодезические в пространстве-времени, т. е. определить движение частиц в гравитационном поле.

В данной точке квадратичную форму (1) можно диагонализовать и привести ее к метрике Минковского8.2.

В общем случае можно разложить $ g_{ik}$ в ряд Тейлора в окрестности точки $ x_0$

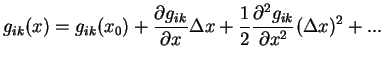
$\displaystyle g_{ik}(x)=g_{ik}(x_0)+{\partial g_{ik}\over{\partial x}}\Delta x+{1\over 2} {\partial^2 g_{ik}\over{\partial x^2}}(\Delta x)^2+... $

Преобразованием системы координат в данной точке всегда можно обратить в нуль первые производные $ g_{ik}$. Для этого достаточно перейти в свободно падающую систему отсчета. Но произвольную совокупность всех вторых производных $ g_{ik}$ никакими преобразованиями системы координат уничтожить нельзя.

Если рассматривать квадратичные эффекты, например, относительные ускорения удаленных частиц, то можно заметить приливные силы. Невесомость существует лишь если ограничиться первым порядком по $ \Delta x$. Таким образом, одна частица ``не чувствует'' гравитационного поля, но система с разнесенными массами ``чувствует''. Глобально гравитационное поле всегда можно обнаружить.

Таким образом, в членах первого порядка по $ \Delta x$ эффект гравитации компенсируется ускорением свободного падения -- в этом и состоит точная формулировка принципа эквивалентности. (Более грубая формулировка: ``Силы инерции эквивалентны некоторому полю тяготения''.)

Итак, кривизна пространства характеризуется двадцатью независимыми числами $ R^i_{klm}$. Естественно связать $ R^i_{klm}$ с веществом.

В ньютоновской теории потенциал гравитационного поля определяется плотностью вещества $ \rho\,$[г/см$ ^3$]. Можно перевести плотность вещества $ \rho $ в плотность энергии $ \varepsilon=\rho c^2$. В специальной теории относительности $ \varepsilon$ является 00-компонентой тензора энергии-импульса

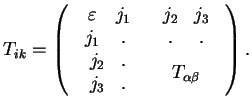
$\displaystyle T_{ik}= \left( \begin{array}{cc} \begin{array}{cc} \varepsilon & ... ...2 & . \\ j_3 & . \\ \end{array} & T_{\alpha\beta} \\ \end{array}\right). $

Тензор $ T_{ik}$ состоит из величин, которые по отношению к трехмерным, чисто пространственным поворотам ведут себя как скаляр $ \varepsilon$, вектор $ \vec{j}$ (поток энергии-импульса на единицу объема) и трехмерный тензор натяжений $ T_{\alpha\beta}$, диагональные члены которого характеризуют давление, а недиагональные -- вязкость.

Мы видим, что вещество характеризуется тензором второго ранга.

Эйнштейн получил уравнения поля в виде

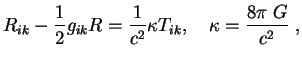
$\displaystyle R_{ik}-{1\over 2}g_{ik}R={1\over{c^2}}\kappa T_{ik},\quad \kappa={8\pi\;G\over{c^2}}\;, $

где $ R_{ik}=g^{lm}R_{limk},\;R=g^{ik}R_{ik}$. Из этих уравнений следует (в случае слабых полей) закон тяготения Ньютона и, кроме того, автоматически выполняются законы сохранения8.3.

В электромагнитной теории заряд сохраняется, но движение заряда произвольно. В ОТО $ T_{ik}$ не может быть любым -- движение должно соответствовать законам механики, т.е. законам сохранения энергии и импульса. Нет метрики, где вещество сначала покоилось, а потом все в целом самопроизвольно начало бы двигаться. Кроме того, оказалось, что из уравнений ОТО получаются не только законы движения материальных точек (т. е. законы механики), но и (с небольшим произволом) законы свободного электромагнитного поля(уравнения Максвелла). Это породило в свое время массу надежд. Казалось, что всю физику можно вывести из ОТО. Однако попытки создать единую теорию поля к успеху не привели.

Число уравнений Эйнштейна равно числу компонент тензора второго ранга, а полное описание пространства задается тензором четвертого ранга $ R_{klm}^i$. В двумерном и трехмерном пространстве-времени задание $ R_{ik}$ однозначно определяет $ R_{klm}^i$, в четырехмерном мире это не так: условие $ R_{ik}=0$ совместимо с $ R_{klm}^i\ne 0$. Это означает, что гравитационное поле может существовать и без источников -- это, например, гравитационные волны.

Еще английский математик Клиффорд высказал идею, что у пространства должна быть собственная упругость. В некотором смысле ОТО является развитием этой идеи. В лагранжиан $ L$ входит кривизна $ R=g^{ik}R_{ik}$:

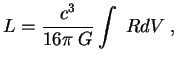
$\displaystyle L={c^3\over{16\pi \;G}}\int\;RdV\;, $

где $ V$ -- четырехмерный объем. (Если задаться таким лагранжианом и лагранжианом других полей и частиц, то при варьировании метрики можно получить уравнения ОТО, что и сделал Гильберт.) Можно наглядно представить себе, что $ L$ описывает упругость пространства, ``стремление'' пространства оставаться плоским. Константа $ c^3/16\pi G$, характеризующая упругость вакуума, велика, и пространство искривлено слабо, из-за того, что велика его упругость.

Может смутить то обстоятельство, что константа $ c^3/16\pi G$ размерна, поэтому непонятно, относительно чего она является большой. В безразмерном виде силу гравитационного взаимодействия характеризует константа $ Gm^2/\hbar c$, аналогичная константе электромагнитного взаимодействия $ e^2/\hbar c=1/137$. Из вида константы сразу получаем массу, характерную для гравитационного взаимодействия (так называемая планковская масса, сравните аналогичные рассуждения о слабом взаимодействии и о массе $ W$-бозона в разделе 7.4):

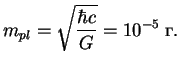
$\displaystyle m_{pl}=\sqrt{{\hbar c\over G}}=10^{-5}\;\mbox{г}. $

Характерная квантовая длина этой массы:

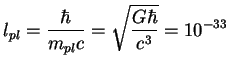$\displaystyle l_{pl}={\hbar\over{m_{pl}c}}=\sqrt{{G\hbar\over{c^3}}}=10^{-33}\;$см$\displaystyle . $

Легко убедится, что $ l_{pl}$ совпадает как раз с гравитационным радиусом $ r_{g}$ для планковской массы. Таким образом, искривление пространства велико на расстоянии $ l_{pl}$ от массы $ m_{pl}$. Для известных элементарных частиц $ m\sim 10^{-24}\,{\mbox г}\ll m_{pl}$, $ l\sim 10^{-13}\,{\mbox см} \ll l_{pl}$, т. е. эффекты гравитации и искривления пространства в объеме известных элементарных частиц чрезвычайно малы. Это и доказывает большую упругость вакуума.

Нельзя ли получить упругость пространства из каких-то более общих соображений? Из квантовой теории мы знаем, что вакуум обладает нулевыми колебаниями, которые, в частности, дают поправки в уровнях атома водорода (Лэмбовский сдвиг). Может быть такие эффекты приводят и к упругости вакуума? Такой подход удалось сформулировать, но при этом оказалось, что в теорию необходимо вводить частицы с массой $ m_{pl}$.

Таким образом, есть два принципиально различных направления:

1) из теории тяготения вывести существование частиц с $ m_{pl}$.

2) из теории частиц получить константу $ G$. (Подробнее см. книги Я.Б.Зельдовича и И.Д. Новикова ``Релятивистская астрофизика'' и ``Теория тяготения и эволюция звезд'').


<< 8.2 Параллельный перенос векторов | Оглавление | 8.4 Гравитационное красное смещение... >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 120]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования