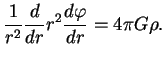<< 1.1 Энергия взаимодействия ... | Оглавление | 1.3 Сферически-симметричные поля тяг... >>
1.2 Векторное поле ускорений, теорема Гаусса, гравитационный потенциал, уравнение Пуассона
Введем понятие векторного поля ускорений ![]() , создаваемых гравитирующими
телами. Одна точечная масса
, создаваемых гравитирующими
телами. Одна точечная масса ![]() создает поле ускорений :
создает поле ускорений :
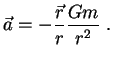
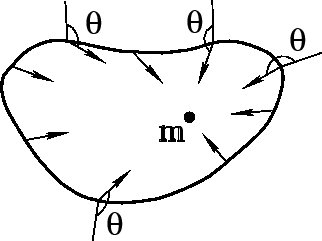
Окружим массу ![]() произвольной замкнутой поверхностью
(рис.1) и вычислим поток
поля
произвольной замкнутой поверхностью
(рис.1) и вычислим поток
поля ![]() через поверхность
через поверхность ![]() :
:
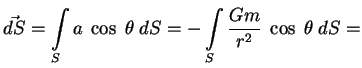 |
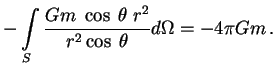 |
Здесь
Если имеется несколько масс
![]() то поле
то поле ![]() является
суперпозицией полей
является
суперпозицией полей
![]() создаваемых этими массами
создаваемых этими массами
Используя это свойство гравитационного поля и окружая поверхностью ![]() несколько масс,
легко получить
несколько масс,
легко получить
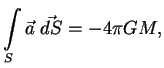
Можно убедиться, что масса, расположенная вне замкнутой поверхности ![]() , не дает
вклада в
, не дает
вклада в
![]() .
.
Таким образом, полный поток векторного поля ![]() равен
равен
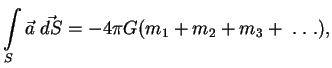
Применим теорему Гаусса к сферическому слою. Пусть ![]() -- сфера радиуса
-- сфера радиуса ![]() , лежащая
внутри этого слоя. Тогда
, лежащая
внутри этого слоя. Тогда
![]() , т.к. внутри
, т.к. внутри ![]() нет масс. Следовательно,
внутри сферического слоя1.1
нет масс. Следовательно,
внутри сферического слоя1.1![]() .
Окружим теперь сферически-симметричную конфигурацию массы
.
Окружим теперь сферически-симметричную конфигурацию массы ![]() поверхностью
поверхностью ![]() .
Тогда
.
Тогда
![]() и
и ![]() . Итак, сферически-симметричная
конфигурация создает поле, эквивалентное полю точечной массы, сосредоточенной в ее
центре.
. Итак, сферически-симметричная
конфигурация создает поле, эквивалентное полю точечной массы, сосредоточенной в ее
центре.
Для малого объема ![]() можно написать
можно написать
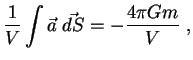
Мы получили уравнение Пуассона -- основное уравнение теории потенциала. Дифференциальный
оператор
![]() называют лапласианом. В декартовых координатах
называют лапласианом. В декартовых координатах
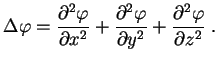
В сферических координатах (
![]() )
)
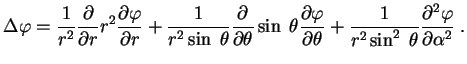
Итак, для сферически-симметричного распределения плотности
<< 1.1 Энергия взаимодействия ... | Оглавление | 1.3 Сферически-симметричные поля тяг... >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |