Астронет > 4.3 Поведение плотности и температуры вблизи поверхности горячей звезды

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Физические основы строения и эволюции звезд

<< 4.2 Коэффициент теплопро... | Оглавление | 4.4 Критическая светимость >>

4.3 Поведение плотности и температуры вблизи поверхности горячей звезды

Зависимость $\rho$ и от радиуса определяется уравнениями:

1) ${dP\over dr}=-{Gm(r)\over r^2}\,\rho$ -- уравнение гидростатики,

2) $L(r)=-4\pi\,r^2\,{c\over 3\varkappa\rho}\,{d\varepsilon_r\over dr}$ -- уравнение теплопроводности, где $L(r)=H_r4\pi r^2$ -- светимость, т.е. полный поток энергии через сферу радиуса . Так как $P_r=\varepsilon_r/3$ , перепишем последнее уравнение в виде

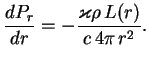
$\displaystyle {dP_r\over dr}=-{\varkappa\rho\,L(r)\over c\,4\pi\,r^2}.$

Если бы ядерная энергия каждой единицы массы звезды $\varepsilon\;($ эрг г $\cdot$ с выделялась одинаково, так что $\varepsilon=$ const по звезде и $L(r)=\varepsilon\;m(r)$ , то мы получили бы, что

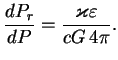
$\displaystyle {dP_r\over dP}={\varkappa\varepsilon\over cG\,4\pi}.$

Поскольку приближенно

$\displaystyle \varkappa=\varkappa(P_r/P),$

(4.3)

мы получим решение, положив, например,

$\displaystyle P_r/P=$ const $\displaystyle .$

Несколько десятков лет назад, когда мало знали об источниках ядерной энергии, астрофизики занимались задачами подобного рода, однако сейчас это представляет чисто исторический интерес.

Вблизи поверхности звезды $m(r)=M,\;L(r)=L$ -- полная светимость звезды и

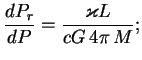
$\displaystyle {dP_r\over dP}={\varkappa L\over cG\,4\pi\,M};$

это хорошее приближение потому, что постоянно выделение энергии $\varepsilon$ , а потому, что у поверхности $M-m\ll M$ .

При , и const $\cdot P$ . Из (4.3) получим $\varkappa=$ const, а из уравнения гидростатики

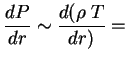$\displaystyle {dP\over dr}\sim{d(\rho\;T\over dr)}=$ const $\displaystyle \cdot\rho$

имеем

const $\cdot(R-r)$ . Из

const следует $\rho\sim T^3 =$ const ${(R-r)}^3$ . Таким образом, независимо от того, как распределены источники ядерной энергии вблизи центра звезды, следует асимптотическое распределение

и $\rho$ вблизи поверхности. Заметим только, что на краю $T\ne 0$ , а $T\to T_{eff}$ . Поэтому наши асимптотики верны при $T>T_{eff}$ , где $T_{eff}$ определяется соотношением

$\displaystyle L=4\pi\sigma\,T_{eff}^4\,R^2,$

т.е. не в атмосфере и не в короне.

<< 4.2 Коэффициент теплопро... | Оглавление | 4.4 Критическая светимость >>

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы

См. также:

Переработка вещества в Кассиопее А

NGC 7789: Роза Каролины

Планетарная туманность NGC 2818 от Хаббла

Научная конференция "Наблюдаемые проявления эволюции звезд" в САО РАН

Планетарные туманности

Прошлые и будущие звёзды Андромеды

Туманность Ожерелье

Все публикации на ту же тему >>

Обсудить эту публикацию

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце