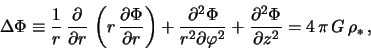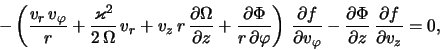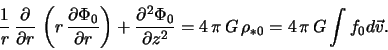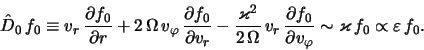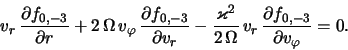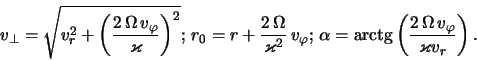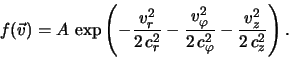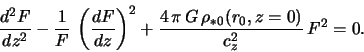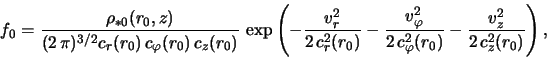---

<< 2. Динамика звездного диска | Оглавление | 2.2 Динамика возмущений ... >>

Разделы

• 2.1.1 Исходные уравнения
• 2.1.2 Равновесная функция распределения звезд

---

2.1 Равновесие

2.1.1 Исходные уравнения

Характерное время, в течение которого параметры движения отдельной звезды могут заметно измениться благодаря парному гравитационному взаимодействию с другими звездами в дисках плоских галактик, намного больше времени существования этих систем [61]. Поэтому структуру и динамику звездных дисков галактик с хорошей точностью можно описывать с помощью бесстолкновительного кинетического уравнения. В декартовых координатах это уравнение имеет вид

где -- функция распределения звезд в шестимерном фазовом (координатно-скоростном) пространстве, -- гравитационный потенциал. Подчеркнем, что векторную форму мы использовали исключительно для краткости записи, и при переходе к другой системе координат вид уравнения (2.1.1) изменится^2.1.

Звездные диски галактик в значительной мере обладают осевой симметрией, что является естественным следствием их вращения. По этой причине для решения многих проблем динамики звездного диска удобно пользоваться уравнением (2.1.1), записанным в цилиндрических координатах [1]:

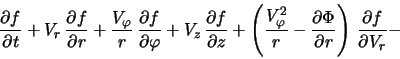
Уравнение (2.1.2) могло бы полностью описывать динамику звездного диска, если бы был задан гравитационный потенциал . Величина последнего определяется распределениями пространственных плотностей всех подсистем галактики -- в основном звезд диска , сфероидальной и плоской газовой . В объеме, занятом звездным диском, величина мала по сравнению с , даже если масса диска сравнима с массой гало (см. п. 1.3.2). Поэтому, интересуясь динамикой звездного диска, можно в первом приближении потенциал гало считать внешним, не зависящим от времени.

В осесимметричных задачах или системах без газа^2.2 гравитационный потенциал, определяющий динамику звездного диска, практически можно считать самосогласованным и тем самым связать величины и через объемную плотность звездного диска уравнением Пуассона

где -- гравитационная постоянная, а величины и связаны очевидным соотношением

Выше уже упоминалась относительная малость амплитуд неосесимметричных возмущений плотности звездного диска. Кроме того, если отвлечься от упомянутых особенностей, распределения различных величин в дисках практически не изменяются в течение временных промежутков порядка нескольких оборотов диска. И тем самым функцию распределения звезд диска можно представить в виде суммы стационарной осесимметричной и "возмущенной" компонент.

Как уже отмечалось в обзоре наблюдательных данных (см. разд. 1.1), основным движением звезд в диске является их вращение вокруг оси симметрии плоской галактики. В соответствии с этим удобно выделить угловую скорость вращения диска

и ввести остаточную скорость соотношениями

Нетрудно видеть, что такое преобразование приведет исходное кинетическое уравнение (2.1.2) к виду

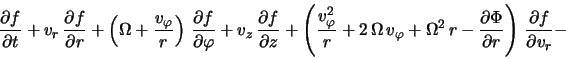
где -- эпициклическая частота (частота малых колебаний звезд диска в радиальном направлении -- см.разд. 1.1).

2.1.2 Равновесная функция распределения звезд

Равновесная (стационарная и осесимметричная) компонента функции распределения звезд диска, согласно (2.1.7), должна удовлетворять уравнению

где -- стационарная осесимметричная часть гравитационного потенциала, описываемая уравнением Пуассона

Система уравнений (2.1.8), (2.1.9) самосогласованна и в соответствии с приведенными выше замечаниями может служить для определения функций и . Она довольно сложна, и для дальнейшего продвижения в решении поставленной нами задачи необходимо использовать приближения, основанием для применения которых должны быть данные наблюдений.

Из этих данных в первую очередь следует, что характерная полутолщина звездного диска много меньше его радиуса . Это означает, что в уравнении (2.1.9) и в простейшем приближении однородного по толщине диска из (2.1.9) вытекает оценка частоты колебаний звезд поперек плоскости диска [см. (1.1.4)]:

где -- равновесная поверхностная плотность звездного диска. Очевидно, что для заданного значения величина при . В этом же пределе частота колебаний звезд в плоскости диска остается конечной величиной [186]. Поэтому в теории, изучающей структуру достаточно тонких звездных дисков, появляется малый параметр [см. оценку (1.1.6)]

Из приведенных выше рассуждений следует, что амплитуда колебаний звезд поперек плоскости диска есть величина порядка , а -компонента их скорости . Поэтому в уравнении (2.1.8) операторы и . С другой стороны, используя уравнения движения отдельной звезды поперек плоскости диска, видим: . Поэтому связанная с -движением звезд часть кинетического уравнения (2.1.8) имеет вид

Из данных наблюдений также следует (см. п. 1.1.1), что характерные дисперсии компонент остаточных скоростей звезд [см. (2.1.6)] малы по сравнению со скоростью вращения звезд диска вокруг центра масс галактики:

где , . Малая величина этого параметра означает, что ; и, следовательно, членами и в уравнении (2.1.8) можно пренебречь. Приближение, в котором указанными членами пренебрегают, называется эпициклическим^2.3. Членом мы пренебрегать не будем, поскольку характерные масштабы радиальной неоднородности параметров диска за пределами его центральной части малы по сравнению с расстоянием до центра диска [8].

Приближение, определяемое неравенством (2.1.13), дает основание заключить, что равновесие диска в радиальном направлении обусловлено балансом центробежной и равновесной гравитационной сил

с точностью до членов .

Из приведенной выше оценки следует, что зависящая от часть равновесного гравитационного потенциала . Именно эта величина и определяет порядок по параметру зависящей от -координаты компоненты угловой скорости вращения диска. Действительно, так как полная , где , из условия равновесия диска (2.1.14) получим

и, следовательно,

За вычетом этого вклада и [см. (2.1.12)] оставшаяся совокупность членов в (2.1.8) есть

Полученные результаты, оценивающие согласно (2.1.12), (2.1.16), (2.1.17) порядки членов кинетического уравнения по малому параметру , позволяют перейти к решению поставленной нами задачи определения и методом последовательных приближений. Для реализации этой возможности заметим, что из элементарной оценки следует и, следовательно, . Поэтому разложения искомых функций и в ряды по степеням параметра должны иметь вид

где ; . Разложение по четным степеням обусловлено тем, что его зависимость от определяется только параметром толщины диска . Это утверждение справедливо и для , но необязательно должно выполняться для .

Подставим разложения (2.1.18),(2.1.19) в исходную систему уравнений (2.1.8), (2.1.9). Тогда в двух главных порядках по параметру получим

где

Если бы проекция траектории звезды на плоскость представляла собой окружность, то благодаря стационарности и осесимметричности равновесного состояния диска величина

была бы интегралом движения. Реально же радиальная координата звезды является медленно меняющимся (в связи с тем, что ) параметром. Поэтому приближенно сохраняющейся величиной должен быть адиабатический инвариант [52] и для решения приведенной выше системы уравнений удобно перейти от переменных к переменным типа действие-угол [186]:

В этих переменных система (2.1.20), (2.1.21) примет вид

Отсюда видно, что не зависит от переменной . Поскольку определение и является нашей задачей, проинтегрируем (2.1.28) по полному периоду изменения величины . В результате получим

Перейдем теперь к переменным ,, , связанным с величинами , , соотношениями

Как будет видно из содержания следующего раздела, величина имеет смысл амплитуды радиальной скорости звезды, представляет собой радиус круговой орбиты центра эпицикла звезды, а величина является фазой движения звезды по эпициклу. Поскольку в рамках используемого нами эпициклического приближения , то в (2.1.30), (2.1.31) следует полагать , .

Нетрудно видеть, что в новых переменных (2.1.31) уравнение (2.1.29) приобретает вид

С учетом уравнения (2.1.27) отсюда следует искомая равновесная функция распределения звезд

Это означает, что в рамках используемых нами приближений (эпициклического и главного порядка по параметру ) величины , , являются интегралами движения.

Конкретный вид этой функции должен быть определен на основании дополнительных данных. Непосредственно построить функцию распределения , исходя из наблюдений, в настоящее время представляется возможным только в солнечной окрестности Галактики. Неравенство дисперсий скоростей звезд Галактики в трех взаимно перпендикулярных направлениях является непреложным наблюдательным фактом (см. п. 1.1.4). Имеется ряд аналитических аппроксимаций наблюдаемых распределений скоростей звезд, которые согласуются с наблюдениями только в ограниченных интервалах скоростей (обзор литературы дан Шацовой [187]). Наиболее известно распределение Шварцшильда, которое представляет собой анизотропное максвелловское:

Были предприняты большие усилия для того, чтобы, с одной стороны, обосновать этот закон теоретически [188,189], а с другой -- устранить противоречия с наблюдениями путем увеличения числа и точности наблюдений. В итоге можно сказать, что лишь для малых и средних скоростей звезд удается получить удовлетворительное согласие закона (2.1.34) с наблюдениями. Для области больших скоростей расхождения существенны [187]. Однако, несмотря на наличие определенных трудностей прежде всего теоретического плана, закон Шварцшильда является наиболее популярным в звездной астрономии. Ниже нами будет использоваться распределение в форме (2.1.34)^2.4. В соответствии с этим полагаем

где , параметры , имеют очевидный смысл дисперсий скоростей звезд в радиальном и перпендикулярном к плоскости диска направлениях соответственно, а из (2.1.31) нетрудно видеть, что роль дисперсии скоростей звезд в азимутальном направлении играет величина

Это соотношение между и с хорошей точностью соответствует имеющимся данным астрономических наблюдений [56,57].

Вычислим равновесное распределение объемной плотности в диске. Для этого проинтегрируем (2.1.35) по пространству скоростей

где

-- размерная константа [см. (2.1.35)]. Положим теперь, что

Тогда уравнение Пуассона (2.1.22) в главном порядке по малому параметру переходит в уравнение, определяющее функцию :

Нетрудно видеть, что убывающее при решение этого уравнения имеет вид

где параметр

имеет очевидный смысл характерной полутолщины звездного диска, а величина

представляет собой равновесную поверхностную плотность звездного диска.

Суммируем полученные результаты. Равновесная функция распределения звезд в главном порядке по малому параметру и в эпициклическом приближении, определяемом неравенством (2.1.13), имеет вид

где

а распределение равновесного гравитационного потенциала поперек плоскости диска описывается соотношением

Как видно из (2.1.44)-(2.1.46), равновесие диска определяется распределениями следующих параметров: , , , , , , . Однако не все из них независимы. Так, величина однозначно определяется через угловую скорость соотношением (1.1.5), а параметры , , а также , , связаны уравнениями (2.1.36) и (2.1.42) соответственно. Еще одну связь между равновесными параметрами звездного диска могло бы дать уравнение (2.1.14), если бы масса диска в плоских галактиках всегда была много больше массы сфероидальных подсистем. В этом случае мы могли бы связать [а через уравнение Пуассона и ] с угловой скоростью вращения диска . К сожалению, упомянутое условие не выполняется, и поэтому в рамках развитой выше теории имеются четыре независимых параметра, описывающих звездный диск. Как будет видно из дальнейшего, еще две связи между равновесными параметрами звездного диска можно в принципе получить из условий его маргинальной^2.5 устойчивости относительно изгибных возмущений и возмущений в его плоскости. Тогда независимыми и, следовательно, требующими определения из данных наблюдений останутся лишь два параметра. Одним из них обычно полагают уверенно наблюдаемую угловую скорость вращения диска . Другим может быть либо одна из дисперсий скоростей звезд ( ) в диске, либо его поверхностная плотность . Величина последней из наблюдений уверенно не определяется, однако из данных по многоцветной фотометрии звездных дисков известно, что за пределами центральной ( ) части диска [8,10].

В этом разделе мы, следуя Вандервоорту [186], построили довольно простую модель звездного диска. Более сложные модели структуры диска поперек его плоскости можно найти, например, в упоминавшейся уже работе Вандервоорта и работе Бакола [190]. В последней, в частности, учтен вклад объемной плотности звезд сфероидальной подсистемы (см. также работу [191]). Мы их, однако, описывать не будем. Во-первых, потому, что довольно тонкие детали моделей весьма трудно сравнивать с данными наблюдений. Во-вторых, потому, что задача построения теории устойчивости этих моделей звездных дисков относительно как изгибных возмущений, так и возмущений в их плоскости пока не решена, и тем самым целостного понимания динамики звездного диска в рамках таких моделей не возникает.

---

<< 2. Динамика звездного диска | Оглавление | 2.2 Динамика возмущений ... >>

Публикации с ключевыми словами: аккреционный диск - диск, галактический - гидродинамика - спиральная структура Публикации со словами: аккреционный диск - диск, галактический - гидродинамика - спиральная структура
См. также: Искривленный диск NGC 4753 Аккреционный диск черной дыры: визуализация Дважды искривленный мир двойных черных дыр Спиральный диск вокруг черной дыры В центре спиральной галактики NGC 3521 Массивная черная дыра разрывает пролетающую звезду Ультрафиолетовые кольца M31 Все публикации на ту же тему >>