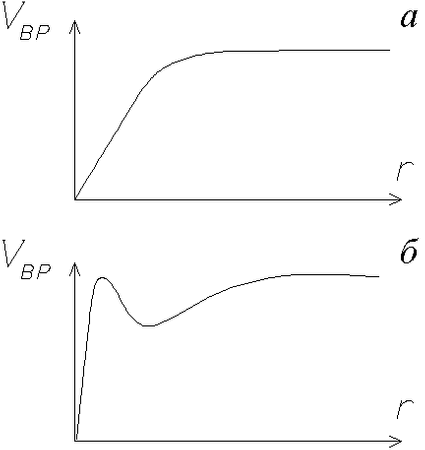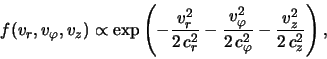---

<< 1. Данные наблюдений | Оглавление | 1.2 Газовые диски плоских ... >>

Разделы

• 1.1.1 Распределение поверхностной плотности
• 1.1.2 Структура диска поперек его плоскости
• 1.1.3 Вращение диска
• 1.1.4 Дисперсия скоростей звезд

---

1.1 Звездные диски плоских галактик

Большинство наблюдаемых галактик могут быть в соответствии с классификацией Хаббла отнесены к плоским. Эти галактики обладают ярким и довольно тонким вращающимся диском с теми или иными структурными особенностями (спирали, перемычки, кольца и т.п.) и сфероидальной подсистемой. Дисковая подсистема обычно состоит из довольно массивного звездного диска и существенно менее массивного газового. Приведем здесь необходимый для дальнейшего изложения (гл. 2-4) краткий обзор основных характеристик подсистем плоских галактик. Более подробное изложение данных наблюдений по плоским галактикам можно найти, например, в книгах Воронцова-Вельяминова [3], Горбацкого [4], Засова [5] (см. также обзор Засова [6]), а по Галактике -- в книге Марочника и Сучкова [7].

1.1.1 Распределение поверхностной плотности

Усредненное в азимутальном направлении распределение яркости вдоль радиальной координаты в звездных дисках галактик, как правило, хорошо описывается экспоненциальным законом

где характерный масштаб в каждой галактике практически одинаков в разных спектральных диапазонах [8]. Поэтому обычно считают, что и распределение поверхностной плотности в звездных дисках тоже является экспоненциальным

с кпк [9,10]. В частности, в Галактике по данным разных авторов кпк [11-16]. В окрестности Солнца величина поверхностной плотности составляет . Экспоненциальный характер дисков легко обнаруживается, например, в рамках модели образования галактик из однородно вращающейся сферической системы при ее сжатии с сохранением углового момента [10,17]. Имеются и другие, вязкие сценарии эволюции галактик, приводящие к (1.1.2) [18,19].

Отклонения от закона (1.1.1) обычно имеют место как в центральных частях галактик размером [8], так и на их периферии. Первые обусловлены, по-видимому, наличием либо яркого балджа или линзы в центральных областях плоских галактик [8,20], либо "дыры" в центральной части звездного диска [21,22] ^1.1. Другое отклонение от закона (1.1.1) по данным фотометрии галактик, видимых с ребра, состоит в том, что в области яркость диска убывает заметно быстрее, чем по закону (1.1.1). Тем самым звездные диски имеют фактически достаточно резкую границу в радиальном направлении [25]. Есть основания считать, что внешняя граница звездного диска Галактики находится на расстоянии 14 - 15 кпк от центра при кпк [16].

Массы звездных дисков плоских галактик лежат в пределах (эта величина для Галактики составляет ).

1.1.2 Структура диска поперек его плоскости

Объемная плотность вещества (звезд и газа) в дисках галактик максимальна в плоскости их симметрии . С удалением от этой плоскости убывание плотности звездной компоненты диска судя по распределению яркости вдоль -координаты [25] удовлетворительно описывается законом

где -- эффективная полутолщина звездного диска^1.2. Заметим, что при такой зависимости поверхностная плотность звездного диска . Величина в большинстве плоских галактик лежит, по-видимому, в пределах кпк и слабо зависит от радиальной координаты. В частности, аппроксимация данных по в окрестности Солнца в Галактике [12,14] функцией (1.1.3) приводит к оценке кпк.

Выделяют также толстый диск, характеризуемый вертикальным масштабом кпк; его объемная плотность в окрестности Солнца составляет около 2% от плотности дисковой системы [27]. Следует сказать, что дисковую систему обычно разделяют на старый диск (звезды поздних классов) и плоскую подсистему, которая является наиболее тонкой и состоит из газа, пыли и молодых звезд.

Из сравнения характерных масштабов звездных дисков плоских галактик ( ) ясно, что равновесный гравитационный потенциал гораздо резче изменяется в -направлении, чем в радиальном. Поэтому в окрестности плоскости естественно полагать и, следовательно, уравнение Пуассона можно записать в виде . Отсюда в простейшем приближении однородного по толщине диска следует оценка частоты колебаний звезды (или другого объекта) поперек плоскости диска

1.1.3 Вращение диска

Основным движением объектов как звездных, так и газовых дисков галактик является их вращение. Хаотические движения звезд и газовых облаков обычно характеризуются существенно меньшими скоростями, и в первом приближении ими можно пренебречь. В соответствии с этим центробежная сила, приходящаяся на единицу массы на заданном расстоянии от центра диска и компенсирующая градиент общего гравитационного потенциала, оказывается практически одинаковой как для звезд, так и для газовых облаков. Поэтому скорость вращения измеряют, как правило, по межзвездному газу. И приводимое ниже разбиение кривых вращения на два типа в равной мере применимо как к звездному, так и к газовому диску [28].

К настоящему времени опубликованы хорошие обзоры кривых вращения большого числа спиральных галактик (см., например, [29-31]). Имеются подробные данные по кривой вращения Галактики [32-39]. Из этих результатов следует, что кривые вращения плоских галактик можно разделить на два типа.

Первый из них характеризуется почти твердотельным вращением центральной части диска ( ), с удалением от центра диска постепенно переходящим в кривую вращения типа "плато" [ const]. На дальней периферии такого диска величина может медленно расти, убывать или оставаться приближенно постоянной (M 33, NGC 157, 300, 681, 1055 и др. -- см. рис. 1.1,а). Такие кривые вращения можно условно назвать "одногорбыми".

Другой тип кривых вращения (в дальнейшем называемых "двугорбыми") характерен тем, что в центральной части диска вместо пологого участка почти твердотельного вращения имеет место резкий рост в области кпк, затем следует область убывания , после чего вновь возрастает и выходит на плато, как и у галактик с одногорбыми кривыми вращения. Весь внутренний "горб" кривых вращения этого типа как бы накладывается на участок почти твердотельного вращения галактик с одногорбыми кривыми (см. рис. 1.1,б). При этом абсолютная величина на внутреннем горбе обычно мало отличается от уровня на плато. К этому типу можно уверенно отнести кривые вращения Галактики [32,35], галактик М31 [40], М81 [41] и многих других.

До недавнего времени почти все галактики считались обладающими одногорбыми кривыми вращения. Однако с возрастанием разрешающей способности наблюдений в ряде из них отчетливо проявилась двугорбость кривых вращения -- например, в галактиках NGC 1566, 2590, 2608, 2708, 3200, 4321, 1553 и др. [29,30,42,43]. Действительно, нетрудно видеть, что интервал между центром диска и внутренним горбом кривой вращения ( кпк) уже на расстоянии, большем Мпк, виден под углом, меньшим 10 угловых секунд. По этой причине выявление внутренних горбов на кривых вращения не очень близких галактик представляет собой довольно сложную наблюдательную задачу.

В 1986-1992 гг на 6-метровом телескопе (САО) была реализована наблюдательная программа по исследованию вращения внутренних областей спиральных галактик [44-48]. Среди изученных объектов по крайней мере у половины кривая вращения может иметь локальные экстремумы.

Причина двугорбости кривых вращения плоских галактик окончательно не ясна. Укажем, однако, два варианта объяснения этого феномена. Во-первых, концентрированное и в то же время массивное центральное образование (балдж) в не очень плотном диске создает в своей внешней части такой градиент гравитационного потенциала, в котором величина должна убывать [49]. Если же такой балдж еще и сплюснут (типа линзы), то может убывать быстрее, чем по кеплеровскому () закону. На эту возможность впервые было указано в работе [50], а подробное ее обсуждение содержится в монографии Фридмана и Поляченко [2]. Другой вариант был предложен Засовым [21] (см. также -- [22]) и состоит в том, что плотный диск с "дырой" в центральной его части позволяет создать двугорбую кривую вращения даже при относительно умеренной концентрации плотности балджа в центре.

Типичные значения максимальной скорости вращения галактик лежат в пределах км/с. Для Галактики эта величина составляет км/с.

Интересной особенностью многих галактик является неубывание кривой вращения на далекой периферии ( ), где плотность вещества диска уменьшается на порядок и больше. Так, например, у Галактики не обнаруживается заметного уменьшения величины вплоть до кпк [51,38], а возможно, и до кпк [39]. Впрочем, кривая вращения строится по наблюдениям газа, и можно поставить вопрос о правомерности приравнивания скоростей для газовой и звездной составляющих.

Вернемся теперь к вопросу об отклонениях движения объектов диска от чисто круговых траекторий, характеризуемых радиусом орбиты const и угловой скоростью . Пусть равновесный гравитационный потенциал, создаваемый распределением всего вещества галактики в ее плоскости, есть , а орбитальный момент объекта единичной массы . Тогда движение такого объекта в радиальном направлении происходит в эффективном гравитационном потенциале 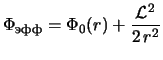[52]. Соответствующее уравнение движения имеет вид

Однако в точке минимума (круговая орбита )

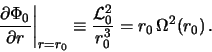
Поэтому при уравнение движения принимает вид

откуда следует, что движение рассматриваемого объекта в радиальном направлении при малых оказывается гармоническим и характеризуется частотой

называемой эпициклической. Отметим, что в случае твердотельного вращения , для кеплеровского вращения частоты вращения и эпициклическая совпадают, а на участках кривых вращения типа "плато" .

Интересно хотя бы в первом приближении оценить соотношение частот колебаний звезды в плоскости диска (1.1.5) и поперек ее плоскости (1.1.4). Очевидно, что в центральной части диска, где распределение вещества с учетом балджа близко к сферическому, эти частоты сравнимы. Однако на периферии галактики это не так. Действительно, внутри сферы радиусом масса экспоненциального диска равна и, следовательно, по порядку величины

(в этих оценках полагаем массу сфероидальной подсистемы порядка или меньше массы диска). Тогда

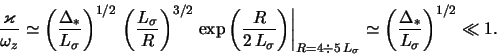
В частности, по данным наблюдений в окрестности Солнца в Галактике [12] . Этот результат позволит нам при построении теории равновесия и устойчивости звездного диска рассматривать отношение как малый параметр.

1.1.4 Дисперсия скоростей звезд

Звезды в дисках плоских галактик движутся, испытывая отклонения от круговых орбит. В галактиках без бара^1.3 или вдали от него эти отклонения невелики и могут характеризоваться наличием у звезды компонент , , пекулярной (за вычетом вращательной ) скорости. Распределение звезд по остаточным скоростям удовлетворительно описывается шварцшильдовской функцией распределения (максвелловские распределения по каждой из компонент скоростей с различными "температурами"):

в которой дисперсии скоростей , , являются функциями координаты .

В солнечной окрестности Галактики по данным Вилена [53,54] в среднем по звездам всех спектральных классов^1.4 км/с; км/с; км/с ( ). Близкие результаты содержит и работа Огородникова и Осипкова [55]. Наблюдаемое соотношение между и (см. также [56,57]) близко к вытекающему из условия равновесия диска (см. гл. 2). Величина отношения зависит от возраста звезд [57]. Для наиболее старых (возраст которых не меньше лет звезд диска Галактики [53]. Наблюдательные данные по молодым звездам дают [58-60]. Анизотропия функции распределения (1.1.6) подчеркивает бесстолкновительность звездных дисков галактик [61] и, следовательно, диктует способ описания их динамики с помощью бесстолкновительного кинетического уравнения.

Как отмечалось выше, скорость вращения вещества диска существенно превышает величины остаточных скоростей звезд, характеризуемых дисперсиями , , (так, в окрестности Солнца км/с). Этот факт позволит нам в дальнейшем воспользоваться эпициклическим приближением (главным порядком по малому параметру ).

Из-за трудностей наблюдательного определения дисперсий скоростей звезд объем данных по радиальной зависимости величины за пределами солнечной окрестности Галактики и в других галактиках невелик. В целом величина дисперсии убывает с удалением от центра и практически всегда убывание дисперсии с ростом оказывается более медленным, чем для поверхностной плотности звездного диска [62]. С удалением от центра отношение , как правило, уменьшается. Для плоских галактик в области типичные значения параметра составляют [42,63-67].

В заключение раздела упомянем о том, что удалось выделить слабые диски в экваториальной плоскости -галактик. Светимость таких дисков составляет несколько процентов от общей светимости, и они являются достаточно толстыми ( от размера -галактики) [68,69].

---

<< 1. Данные наблюдений | Оглавление | 1.2 Газовые диски плоских ... >>

Публикации с ключевыми словами: аккреционный диск - диск, галактический - гидродинамика - спиральная структура Публикации со словами: аккреционный диск - диск, галактический - гидродинамика - спиральная структура
См. также: Аккреционный диск черной дыры: визуализация Дважды искривленный мир двойных черных дыр Спиральный диск вокруг черной дыры В центре спиральной галактики NGC 3521 Массивная черная дыра разрывает пролетающую звезду Ультрафиолетовые кольца M31 Близкая массивная спиральная галактика NGC 2841 Все публикации на ту же тему >>