Астронет > Размерности и подобие астрофизических величин

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Размерности и подобие астрофизических величин << § 1.1 Размерности астрофизических величин | Оглавление | § 1.3 Подобие и моделирование >>

§ 1.2 Астрофизические формулы и П-теорема

Одна из основных задач астрофизики - нахождение соотношений, связывающих между собой параметры небесных тел. Пусть, например, звезда имеет некоторую определенную массу. Какова ее светимость? Может ли эта величина быть произвольной, или она имеет одно или несколько определенных значений? Различаются ли светимости звезд с одной массой, но с разными радиусами и т. д.? Как правило, в астрофизике подобные зависимости имеют статистический характер. Скажем, если считать, что светимость звезды данного типа однозначно определяется массой, то на самом деле имеется некоторый разброс светимостей около среднего значения. Правда, отчасти этот разброс связан с неизбежными ошибками наблюдений как в определении светимости, так и в определении массы. Но отчасти он и вполне реален, поскольку разные звезды одного и того же типа могут хотя бы немного различаться химическим составом, вращением, магнитным полем. Разумеется, при теоретическом выводе соотношений эти различия, в принципе, могут быть учтены.

Астрофизические соотношения могут быть получены из наблюдений, если собран достаточно большой статистический материал, и из теории, если мы достаточно хорошо понимаем физические процессы, лежащие в основе того или иного явления. Правда, чаще всего и наблюдений недостаточно, и физика явления частично остается неясной. Наблюдательные данные обычно представляют в форме графиков или таблиц. Кривые на графиках или табличные данные можно описать с помощью аппроксимационных, или, как их часто называют, эмпирических формул. Например, зависимость спектрального потока излучения F_ν от частоты для многих объектов может быть аппроксимирована степенной формулой

$F_\nu \sim \nu^{-\alpha}$ (1.5)

в определенном интервале частот. Здесь спектральный индекс α - величина, подбираемая так, чтобы кривая (1.5) наилучшим образом соответствовала бы наблюдениям излучения данного объекта в определенном интервале частот. Как правило, эмпирические формулы не универсальны в том смысле, что они применимы лишь к определенным интервалам условий. Например, соотношение (1.5) может быть справедливо в радиодиапазоне и не годится для описания оптического излучения; оно может быть использовано для разных диапазонов излучения одного объекта, но при отдельном подборе параметра α для каждого диапазона.

Часто оказывается, что найденная вначале эмпирическая формула оказывается затем непригодной по мере того, как накапливаются и уточняются наблюдательные данные. Но несмотря на все эти недостатки, определение эмпирических зависимостей играет огромную роль в астрофизике, позволяя в сжатом виде описать данные наблюдений, показывая направление дальнейшего поиска зависимостей, давая возможность более точной физической интерпретации явлений и более надежного сопоставления теории и наблюдений. Заметим, что, как правило, эмпирические формулы представляют собой простые алгебраические (степенные) соотношения.

В результате теоретического анализа мы тоже получаем формулы, описывающие связи между разными астрофизическими параметрами. Сопоставление теоретических и эмпирических зависимостей служит основным методом проверки правильности нашего понимания физики явления. Теоретические формулы, разумеется, много сложнее эмпирических, поскольку здесь приходится учитывать много различных, более или менее произвольно задаваемых факторов и условий. Но и здесь мы часто стараемся упростить формулы, привести их к наиболее удобному виду алгебраических степенных зависимостей.

Наконец очень часто бывает и так, что интуитивно чувствуется необходимость зависимости между параметрами небесных тел, - но ни теория, ни наблюдения пока этой зависимости, даже в ее простейшей форме, выявить не могут. И здесь естественно возникает вопрос - можно ли с помощью анализа размерностей изучить аппроксимацнонные эмпирические формулы и получить теоретические зависимости?

В самом деле, соображения размерности позволяют получить соотношения между параметрами на основе лишь очень общих представлений о физических свойствах небесных тел и тогда, когда детальная картина процессов остается не ясной. Часто одной интуиции достаточно, чтобы найти из соображений размерности нужное нам соотношение. Но и в тех случаях, когда мы можем получить теоретическим путем те или иные формулы, соображения размерности позволяют лучше понять их смысл, отбросить второстепенные факторы и значительно их упростить. Зная эмпирические формулы (которые обычно не учитывают размерностных соображений), можно из условий размерности получить более точные формулы.

Во многих случаях соотношения, полученные на основе соображений размерности, ничуть не хуже "точной" теории. Например, для теоретического анализа часто приходится учитывать геометрические факторы, которые, как правило, остаются неопределенными. В рамках анализа размерностей мы обычно отвлекаемся от этих факторов, оставляя лишь те физические параметры, которые действительно определяют суть явления и вместе с тем могут быть достаточно, надежно сравнены с наблюдениями.

Мы надеемся, что все последующее изложение и рассмотрение конкретных проблем позволит читателю ясно понять достоинства и недостатки метода анализа размерностей в специфических астрофизических условиях.

Применение метода анализа размерностей основано на принципе размерной однородности, математическим выражением которого является П-теорема (иногда, особенно в литературе на английском языке, называемая также теоремой Бэкингема). Принцип размерной однородности был сформулирован еще Фурье, а первые систематические применения метода анализа размерностей были даны Рэлеем. Вероятно, каждому читателю принцип размерной однородности в его простейшей форме уже известен: все уравнения, описывающие любые физические явления, имеют такую форму, что входящие в них слагаемые обладают одинаковой размерностью, а аргументы трансцендентных функций (тригонометрических, логарифмичеческнх и т. п.) безразмерны.

Сказанное относится именно к физическим уравнениям. Эмпирические формулы часто записываются без соблюдения принципа размерной однородности п поэтому они справедливы только при определенном масштабе измерения параметров. Принцип размерной однородности сразу следует из требования, чтобы все физические законы и описывающие их уравнения не зависели бы от выбора масштаба единиц измерения.

Строгие математические доказательства принципа размерной однородности и П-теоремы даны в книгах по методу анализа размерностей и подобия. Мы не будем здесь подробно заниматься этой математической теорией. Читатель сможет познакомиться с этими вопросами по упомянутой в предисловии книге Л. И. Седова "Методы подобия и размерности в механике" [2] и по ряду других монографий (см. [3-7]).

Формулировку П-теоремы мы поясним на основе астрофизических примеров. Метод ее применения по существу и есть метод ее доказательства. Надо, правда, заметить, что хотя в теории анализа размерностей и существуют некоторые формальные правила, все же во многих случаях большую роль играет интуиция, необходимость догадываться, как лучше поступить в том пли ином конкретном случае.

Рассматривая какие-либо свойства небесного тела или астрофизического явления, мы прежде всего должны выяснить, какие параметры его характеризуют. Будем называть такие параметры определяющими. Некоторые из них находятся по данным наблюдений (масса, размеры, светимость и т. д.), другие задаются на основании наших представлений о физике явлений (например, химический состав, коэффициент поглощения, наличие быстрых частиц, магнитных полей и т. п.), третьи являются универсальными константами, определяемыми общими физическими законами, описывающими состояние и процессы в данном объекте (постоянная тяготения Ньютона, скорость света, постоянная закона Стефана - Больцмана и др.).

Разумеется, важность и необходимость задания разных определяющих параметров в каждом конкретном случае весьма различна. Какие и сколько определяющих параметров надо выбрать, чтобы адекватным образом охарактеризовать интересующее нас явление, обычно приходится решать на основе опыта пли физической интуиции. Разумеется, если мы имеем достаточно полную теорию рассматриваемого явления, т. е. можем написать описывающую это явление систему уравнений, то эта система сразу же дает нам и весь набор определяющих параметров.

В астрофизике есть много задач, где удается написать сравнительно полные системы уравнений, получить их решения и подробным образом исследовать их. Большого совершенства достигла теория внутреннего строения звезд, теория распространения электромагнитных волн в космической плазме, теория ударных волн. Но и здесь оказывается полезным метод подобия и размерностей. В частности, к теории внутреннего строения звезд и к задаче о распространении ударных волн в звездах впервые метод подобия был применен Л. И. Седовым еще в 1954 г. (изложение см. в [2]).

В настоящей книге мы будем также заниматься теми наиболее часто встречающимися в астрофизике случаями, когда полной системы уравнений написать вообще нельзя, либо она оказывается слишком громоздкой. Поэтому в подобных задачах при выборе определяющих параметров приходится опираться на интуитивные представления о физике явления.

Впрочем, применение метода анализа размерностей существенно и в тех случаях, когда имеется более полная теория. Часто в астрофизике представление о том, что составленная нами система уравнений правильно описывает явление, оказывается обманчивым, поскольку нет уверенности, что учтено все, что нужно. Математическая точность расчета при решении таких уравнений оказывается иллюзорной и может ввести в заблуждение, например, неискушенного в теории наблюдателя. Простые размерностные соотношения, четко определяющие, что учтено и что нет, и имеющие очень прозрачный вид, дают ясное физическое представление об интересующем нас явлении. Много примеров мы приведем в последующих главах.

Вернемся к П-теореме. Пусть у нас есть некоторый набор п определяющих параметров A₁, A₂, ..., A_n с размерностями, обозначаемыми, как обычно, [A₁], [A₂],...,[A_n]. Некоторые из этих величин могут иметь и одинаковые размерности, хотя сами величины либо сильно отличаются по величине, либо вообще описывают физически разные параметры (например, скорость частиц газа и альвеновская скорость).

Из всего набора определяющих параметров можно выделить величины с независимыми размерностями, т. е. такие, что размерность каждой из них не может быть представлена в виде комбинации размерностей других выделенных параметров. Другое определение величин с независимыми размерностями: из них нельзя построить безразмерного комплекса. Очевидный астрофизический пример: масса [М] = г, размер [R] = см и светимость [L] = $\frac{\mbox{г} \cdot \mbox{см}^2}{\mbox{сек}^3}$ . Сразу видно, что из М, R и L нельзя построить безразмерного комплекса. Число параметров с независимыми размерностями не может быть больше числа основных, первичных единиц измерения, но может быть и меньше. Мы условились в астрофизике пользоваться четырьмя основными единицами - длины, массы, времени и температуры, поэтому число параметров с независимыми размерностями не больше четырех. Но этих параметров может быть и меньше, и мы часто будем встречаться с таким набором параметров, из которых только три или даже два являются независимыми по размерности. В дальнейшем в перечислении определяющих параметров независимые по размерности величины будем помещать в начале списка.

Теперь допустим, что мы ищем какое-либо соотношение, связывающее те или иные параметры изучаемого небесного объекта. Пусть этот объект характеризуется набором n определяющих параметров. Запишем искомое соотношение - формулу, связывающую между собой определяющие параметры, в следующем общем виде:

$f(A_1, A_2, ..., A_n) = 0.$ (1.6)

Нахождение явного вида этих соотношений и есть основная задача астрофизики (как и любой другой науки).

Известная П-теорема утверждает, что соотношение (1.6) может быть переписано в виде

$f(\underbrace{1,1,...,1}_{k}; \quad \underbrace{\Pi_{k+1},\Pi_{k+2},...,\Pi_n}_{n-k})=0,$ (1.7)

где через k обозначено число определяющих параметров с независимыми размерностями, а через П обозначены безразмерные .комбинации (в дальнейшем мы их будем называть комплексами) всех величин A₁, A₂, ..., A_n. Выбор безразмерных комплексов П_k+1, П_k+2, ..., П_n должен быть подчинен определенным правилам, хотя он и не является однозначным. Например, надо стремиться к тому, чтобы как можно большее число этих комплексов были бы независимыми, т. е. не могли бы быть сведены один к другому путем возведения в степень или перемножения. Таким образом, сущность П-теоремы заключается в том, что он сводит функцию n размерных параметров к функции меньшего числа n - k безразмерных комплексов. Строгое доказательство и пределы применимости П-теоремы приведены, например, в [2, 3], а также и в других руководствах по применению метода анализа размерностей [4-7].

Метод доказательства основан на принципе размерной однородности - соотношение (1.6) не должно измениться, если мы изменим систему единиц. Поэтому мы можем умножить все размерностные аргументы функции (1.6) на один и тот же множитель без нарушения этого уравнения. Выбирая этот множитель равным 1/A₁ получим первую единицу в (1.7). Поскольку число множителей с независимыми размерностями равно k, то такую процедуру можно проделывать k раз, в результате чего останется в уравнении k единиц и n - k безразмерных комплексов.

Разумеется, вид функции (1.7) тот же, что ив (1.6), методом теории размерностей он не определяется. Анализ размерностей имеет дело только с аргументами этих функций. Тем не менее уже из общего сравнения (1.6) и (1.7) можно сделать ряд важных выводов.

Во-первых, следует подчеркнуть, что уменьшение числа аргументов (от n в (1.6) до n - k в (1.7)) представляет собой существенное упрощение соотношения. По образному выражению Клайна [4], функция одного аргумента может быть табулирована в одной строчке, функция двух аргументов - на странице, таблица функции трех аргументов требует книги, а четырех - библиотеки.

Во вторых, если n - k=1, т. е. если число определяющих параметров всего на единицу больше числа параметров с независимой размерностью, то вместо (1.7) имеем

$f(1, 1, ..., 1; \Pi) = f_1(\Pi) = 0.$ (1.8)

Здесь остается один безразмерный комплекс. Формула (1.8) теперь имеет вид уравнения только для одной величины, решение которого определяет численное значение (одно или несколько) величины П. Часто уравнение (1.8) имеет простую алгебраическую форму и его корень, как правило, оказывается по порядку величины не слишком сильно отличающимся от единицы.

Таким образом, в том важном случае, когда число определяющих параметров на единицу больше числа независимых размерностей, совершенно не зная заранее вида функции, связывающей эти параметры, из одних только размерностных соображений мы можем определить эту функцию с точностью до численного множителя, который часто сравним с единицей. Для более точного определения численного множителя можно использовать наблюдательные данные или метод моделирования.

В-третьих, во многих случаях даже при большем числе определяющих параметров, т. е. при n - k > 1, можно получить искомые зависимости. Рассмотрим случай, когда в (1.7) все безразмерные комплексы П_k+2, ..., П_n, кроме П_k+1, малы по сравнению с единицей. Тогда можно написать:

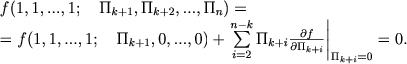
$\begin{array}{l} f(1,1,...,1; \quad \Pi_{k+1},\Pi_{k+2},...,\Pi_n)= \\ = f(1,1,...,1; \quad \Pi_{k+1},0,...,0)+\left.\sum\limits^{n-k}_{i=2} \Pi_{k+i}\frac{\partial f}{\partial \Pi_{k+i}}\right|_{\Pi_{k+i}=0} = 0. \end{array}$ (1.9)

В первом приближении, при П_k+1 << 1 отсюда опять следует соотношение f(1, 1,..., 1; П_k+1, 0, ..., 0) = 0, которое однозначно определяет численное значение единственного "значащего" безразмерного комплекса. Иными словами, если мы можем так сконструировать полный набор (т. е. всех n - k) безразмерных комплексов, что только один из них не мал по сравнению с единицей, то отсюда тоже можно получить зависимость между определяющими параметрами с точностью до постоянного множителя порядка единицы. То же самое имеет место, если какие-либо из комплексов П_k+2, ..., П_n много больше единицы. Тогда в (1.9) можно использовать соответствующее разложение по величинам $\Pi_{k+1}^{-1}$ . Таким образом, если из всего набора безразмерных комплексов имеется только один "значащий" комплекс, величина которого не слишком сильно отличается от единицы в обе стороны, а все остальные комплексы либо много меньше единицы, либо много больше, то этот значащий комплекс должен быть константой, численное значение которой определяется в теории однозначно.

И, наконец, в самом общем случае, когда есть несколько сравнимых по величине безразмерных комплексов, из размерностных соображений можно все же получить искомые соотношения. Однако теперь вместо постоянных коэффициентов появляются меняющиеся величины, изменение которых, впрочем, часто ограничено некоторыми пределами.

<< § 1.1 Размерности астрофизических величин | Оглавление | § 1.3 Подобие и моделирование >>

Мнения читателей [4]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце