10.1 Формулы Ботлингера
Рассмотрим несложную кинематическую модель Галактики, сделав упрощающее предположение, что центроиды движутся вокруг центра Галактики по круговым орбитам. Движение осуществляется вокруг оси симметрии Галактики в плоскостях, параллельных основной плоскости симметрии Галактики. При этом в каждой из параллельных плоскостей вращение происходит одинаково, т.е. функции, описывающие вращение Галактики не зависят от z. Такой тип движения называется баротропным вращением. При этом на закон вращения - зависимость скорости вращения от расстояния до оси вращения Галактики - никаких ограничений не накладывается. Выведем формулы, описывающие наблюдаемые проявления вращения Галактики при сделанных предположениях, следуя Ботлингеру.
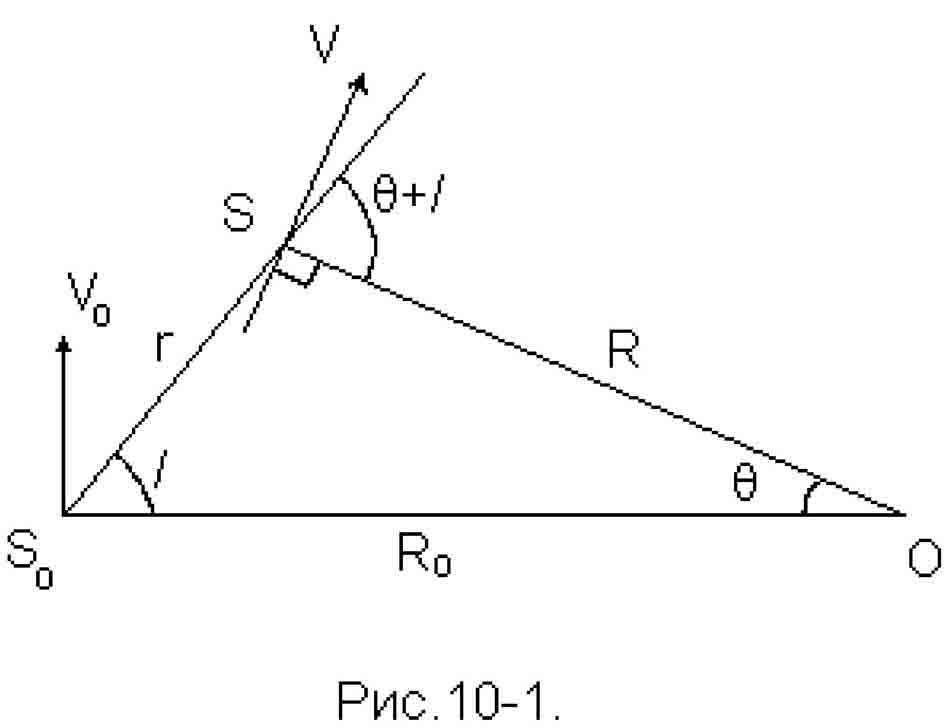
Рассмотрим объект S, лежащий в плоскости Галактики (см. рис. 10-1). Вектор V0 представляет собой линейную скорость кругового движения центроида S0 звёзд, вместе с Солнцем обращающегося вокруг центра Галактики на расстоянии R0 от оси ее вращения. Вектор V - круговая скорость центроида S, находящегося на расстоянии r от центроида S0 и характеризуемого галактической долготой l. Согласно принятой модели векторы V и V0 направлены по касательным к окружностям с радиусами R и R0. Угловые скорости кругового движения на расстояниях R и R0 от оси вращения Галактики будут:
Найдем проекции векторов V и V
0 на луч зрения S
0S. Они, соответственно, равны
V cos[90° - (Θ + l)] и
V0 cos (90° - l) и или, используя (10-1),
ωR sin(Θ + l) и
ω0R0 sin l. Разность этих двух величин - составляющая лучевой скорости, отражающая дифференциальное вращение Галактики:
Воспользуемся теоремой синусов для треугольника S
0OS :
откуда получим:
Подставив синус суммы углов из (10-4) в выражение (10-2) получим формулу Ботлингера для лучевых скоростей:
где множитель
cosb введен для учета галактической широты, так как R есть расстояние точки S от оси вращения, а не от центра Галактики.
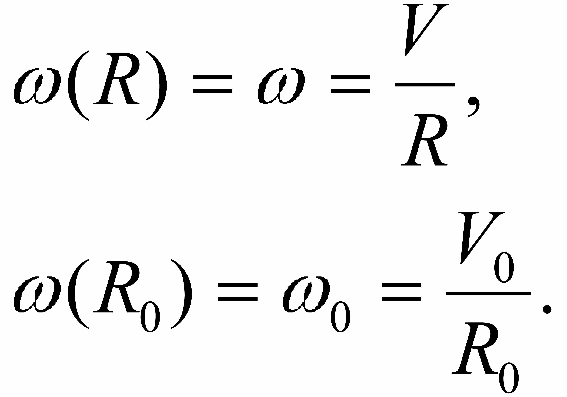
Аналогично можно вывести формулу для тангенциальной скорости vl = 4.74 rμl cos b:
Можно также вывести подобное выражение и для
vb = 4.74 rμb cos b , однако обычно формулы Ботлингера применяются для объектов, лежащих вблизи плоскости Галактики, для которых этот компонент тангенциальной скорости содержит малый вклад от вращения Галактики. Поэтому формула для
vl в исследованиях не применяется.
Напомним, что в (10-5) и (10-6) частота вращения Галактики, часто называемая кривой вращения Галактики, является функцией расстояния от оси вращения Галактики R. Выражения (10-5) и (10-6) являются основными формулами, применяемыми при исследовании кинематических свойств галактического диска. Отметим, что такой важный параметр галактического вращения, как частота вращения Галактики на расстоянии Солнца μ0, может быть определен только с использованием собственных движений из выражения (10-6), тогда как с помощью лучевых скоростей кривая вращения определяется только с точностью до постоянного слагаемого ω0. Поэтому точность определения частоты вращения Галактики целиком определяется точностью системы, используемой для оценки собственных движений.
