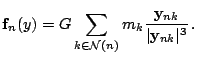<< 3. Разлет без сближений | Оглавление | 3.2. Области и мажоранты >>

3.1. Уравнения движения

Пусть  - система N точек масс , притягивающих друг друга по закону Ньютона. Обозначим через трехмерные векторы скорости и положения . Движение описывается системой дифференциальных уравнений

где

Здесь и ниже  - постоянная тяготения;  - трехмерные векторы относительной скорости и положения;  -  - мерные векторы скорости, положения и ускорения системы ; суммирование производится по целочисленному множеству .

Уравнения (25) имеют форму (5) при , единичной матрице . Если , то, например, равно -компоненте вектора .

---

<< 3. Разлет без сближений | Оглавление | 3.2. Области и мажоранты >>

Публикации с ключевыми словами: Небесная механика - задача n-тел - задача трех тел Публикации со словами: Небесная механика - задача n-тел - задача трех тел

См. также: Саймон Ньюком (1835 -1909) к 175-летию со дня рождения. Наум Ильич Идельсон - 125 лет со дня рождения Методы теории специальных возмущений в небесной механике К 90-летию Александра Александровича Орлова Динамика звездных скоплений Простейшая форма представления градиента гравитационного потенциала небесных тел Эволюция элементов орбит Юпитера и Сатурна на длительных интервалах времени Все публикации на ту же тему >>