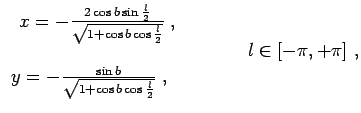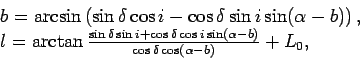<< 3. Работа с ASCII
| Оглавление |
5. Диаграмма Герцшпрунга-Рессела >>
Разделы
4. Построение распределения звезд Hipparcos
на небесной сфере и в пространстве
4.1. Распределение звезд по небесной сфере
С помощью Celestia 2000 можно построить картину распределения выборки звезд на небесной сфере в нескольких проекциях. Наиболее популярная из них - это проекция Хаммер-Айтофа, она была принята в качестве основной в описании Hipparcos и использовалась во многих первых публикациях. Однако графические возможности Celestia довольно ограничены. Например, при числе звезд более 1000 диаграммы строятся не точками, а закрашенными областями, символизирующими звездную плотность. Это число изменить нельзя, а в диаграмме с залитыми областями нет легенды, по которой можно было бы понять абсолютное значение звездной плотности в конкретном месте. Отсутствуют возможности выделения цветом звезд по какому-либо критерию. По этим и многим другим причинам у исследователя возникнет потребность в самостоятельном построении картины распределения звезд по небесной сфере.
Следующие формулы описывают проекцию Хаммер-Айтофа для сферической галактической системы координат:
здесь
, 
- галактические координаты, выраженные в радианах, причем долготу
следует привести в диапазон [-
,+];
, 
- декартовы координаты на плоскости; будет находиться в диапазоне [-1,
+1], а - в диапазоне [-2, +2], начало координат (0, 0) соответствует
направлению на центр Галактики.
Напишем программу, которая строит изображения звезд в этой проекции. В
качестве графической платформы используем стандартную библиотеку BGI,
реализация которой есть в Borland Pascal, Free Pascal4.1, Borland C++. Она настолько проста, что даже
начинающий программист легко адаптирует программу, использующую BGI, под
любую другую систему. Ось 
в этом режиме имеет направление слева направо, а
ось 
- сверху вниз. Верхний левый угол имеет координаты (0,0), а правый
нижний (GetMaxX, GetMaxY). Эту систему координат в нашем изложении мы будем
называть экранной.
Для начала напишем две процедуры Aitoff и Screen. Первая будет переводить сферические галактические координаты в декартовы по формулам (4.1), а вторая - декартовы в экранные.
Листинг 4.1. Процедуры перевода координат
Procedure Aitoff(
l,b:double; { Сферические координаты в
радианах }
var x,y : double); { Декартовы координаты
}
var s : double;
begin
if l>Pi then l:=l-2*Pi;
{ Приведение l в диапазон -Pi до +Pi }
s:=sqrt(1+cos(b)*cos(l/2)); { Знаменатель формул
4.1 }
x:=-2*cos(b)*sin(l/2)/s;
y:=sin(b)/s;
end;
Procedure Screen
(x,y : double; { Декартовы координаты }
X0,Y0: integer;{Экранные координаты начала
декартовой системы}
Scale: double;{Масштаб - сколько точек экрана
на единицу длины}
var u,v : integer);{ Экранные
координаты }
begin
u:=X0+Round(Scale*x);
v:=Y0-Round(Scale*y);
end;
Несколько громоздкой может показаться процедура, отрисовывающая координатную сетку, но никаких алгоритмических сложностей в ней нет.
Листинг 4.2. Процедура, рисующая координатную сетку.
function rad(x:double):double; {
Перевод градусов в радианы }
begin
rad:=x/180.0*Pi;
end;
Procedure AitoffGrid
(Step:integer; { Шаг сетки в градусах
}
X0,Y0 : integer; { Экранные координаты центра
проекции }
Scale : double; { Масштаб - точек на единицу
длины }
Gr : boolean); {Флаг - в градусах или в часах
разметка долготы}
var i,j : integer; {
Переменные циклов for }
l,b : double; { Галактические
координаты }
x,y : double; { Декартовы координаты
}
u,v : integer; { Экранные координаты
}
s : string[5]; { Строка для подписей
}
h : integer; { Для разметки осей }
begin
{ Нанесение сетки меридианов }
i:=-180; {Первый меридиан -180
градусов }
repeat { Цикл по
меридианам }
l:=rad(i); { Перевод в радианы }
j:=-90; { Первая точка меридиана }
repeat { Цикл построения вдоль
меридиана }
{ Вычисление точки меридиана }
b:=rad(j); { Перевод в радианы широты
}
Aitoff(l,b,x,y); { Перевод в декартовы
координаты }
Screen(x,y,X0,Y0,scale,u,v); { Перевод в
экранные коорд. }
{ Если точка первая (j=-90), то помещаем
графический курсор
в точку (u,v) функцией MoveTo, если точка не первая, то
?прочерчиваем? курсором линию из предыдущей точки
в точку (u,v) функцией LineTo }
if j=-90 then MoveTo(u,v) else LineTo(u,v);
j:=j+5; { Шаг 5 градусов обеспечивают гладкий
вид меридиана }
until j>90;
i:=i+step; { Переход к следующему
меридиану }
until i>180;
{ Нанесение сетки параллелей - аналогично
предыдущему }
j:=-90;
repeat { цикл по параллелям
}
b:=rad(j);
i:=-180;
repeat { цикл построения
вдоль параллели }
l:=rad(i);
Aitoff(l,b,x,y);
Screen(x,y,X0,Y0,scale,u,v);
if i=-180 then MoveTo(u,v) else LineTo(u,v);
i:=i+5;
until i>180;
j:=j+step;
until j>90;
{ Задание свойств шрифта (может зависеть от
граф.библ.) }
SetTextStyle(DefaultFont,HorizDir,1);
SetTextJustify(LeftText,BottomText);
{ Подписи меридианов вдоль экватора
}
i:=-180;
repeat
{ Вычисление координаты точки вывода
надписи }
l:=Rad(i);
Aitoff(l,0,x,y);
Screen(x,y,X0,Y0,scale,u,v);
{ Если Gr истина, то разметка в градусах, иначе
- в часах }
if Gr then h:=i
elsebegin h:=i div 15;
if h<0 then h:=h+24;
end;
Str(h,s); { Преобразование значения h в
текстовую строку }
OutTextXY(u+5,v-5,s); { Вывод текстовой строки
}
i:=i+step; { Переход к следующему
меридиану }
until i>180;
{ Изменение выравнивания текста }
SetTextJustify(RightText,BottomText);
{ Подписи параллелей вдоль нулевого меридиана -
аналогично }
j:=-90+step;
repeat
if j<>0 then {
Экватор не подписываем }
begin
b:=Rad(j);
Aitoff(0,b,x,y);
Screen(x,y,X0,Y0,scale,u,v);
Str(j,s);
OutTextXY(u-5,v-5,s);
end;
j:=j+step;
until j>90-step;
end;
Если мы хотим построить проекции звезд Hipparcos в галактической системе координат, то нам необходимо перевести экваториальные координаты, приведенные в каталоге, в галактические. Это можно сделать по формулам
а листинг 4.3 представляет реализацию этих формул.
Здесь
- экваториальные координаты;
= 62
52' 18.295? - наклон галактического экватора;
51' 34.131? 
долгота восходящего узла
галактического экватора;
L
= 32 55' 54.905? - долгота направления на центр Галактики;
- галактические координаты.
Значения констант приведены на эпоху J1991.25. Во второй формуле
подразумевается круговой арктангенс - числитель интерпретируется как синус угла, а знаменатель
- как косинус.
В стандартной библиотеке Pascal могут отсутствовать функции arcsin, arctan2, поэтому мы
сочли целесообразным также поместить здесь код этих функций.
Листинг 4.3. Перевод экваториальных координат в галактические
Function ArcTan2(x,y:double):double;
var z:double;
begin
if y<>0 then
z:=arctan(x/y)
else z:=Pi/2;
if y<0 then z:=z+Pi;
ArcTan2:=z;
end;
Function ArcSin(x:double):double;
begin
ArcSin:=ArcTan2(x,sqrt(1-sqr(x)));
end;
Procedure Galaxy(a,d : double;
var l,b : double);
Var sa,ca,sd,cd : double;
Const Leo = 4.936829261; {
282.85948083}
L0 = 0.57477039907; { 32.931918056 }
si = 0.88998807641; { sin 62.871748611 }
ci = 0.45598379779; { cos 62.871748611 }
begin
a:=a-Leo;
sa:=sin(a); ca:=cos(a);
sd:=sin(d); cd:=cos(d);
b:=arcsin(sd*ci-cd*si*sa);
l:=arctan2(sd*si+cd*ci*sa,cd*ca)+L0;
end;
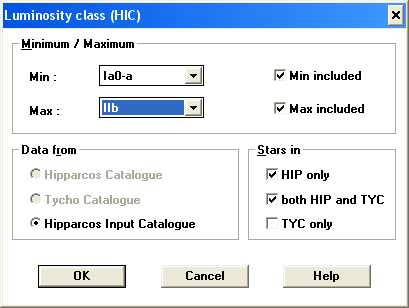
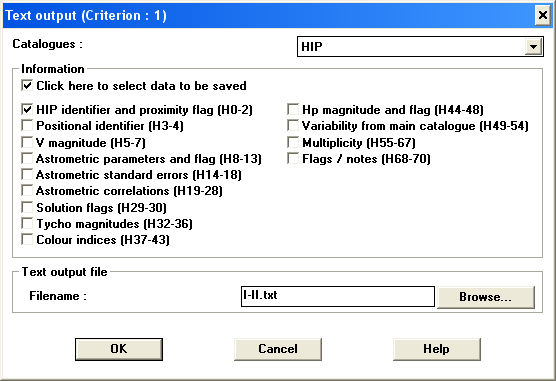
Наконец, перейдем к главной программе. Решим такую задачу: отобразить распределение звезд по небесной сфере I и II класса светимости, причем звезды спектральных классов O, B выделить синим цветом, A - голубым, F, G - желтым, K, M - красным. Для отбора звезд используем программу Celestia и выберем звезды с классом светимости от Ia0-a до IIb (рис. 4.1). Всего должно быть найдено 2248 звезд. Сохраним выборку (Sample) в файл I-II.txt (рис. 4.2).
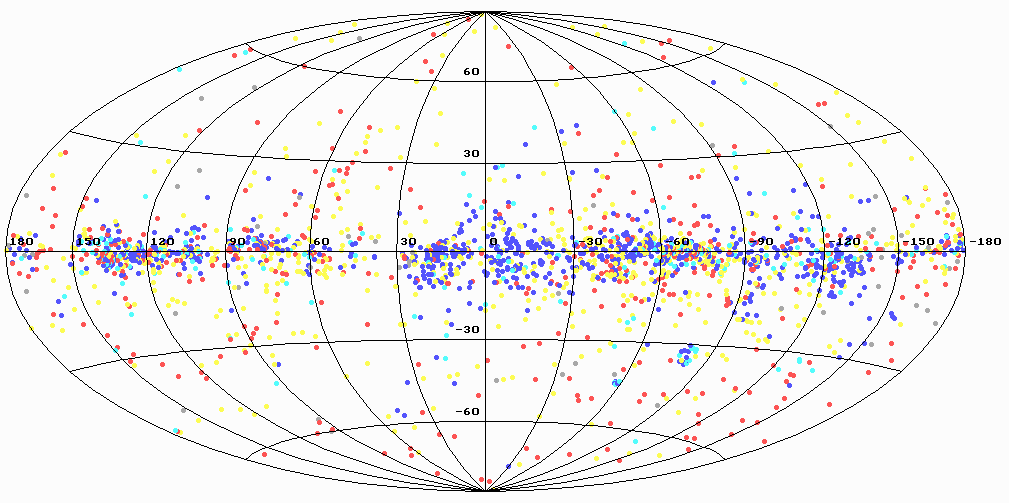
Текст программы, выполняющей построение распределение звезд по небесной сфере, приведен в листинге 4.4, а результат ее работы - на рис. 4.3.
В основном цикле while происходит чтение данных о звезде, проверка, удовлетворяет ли звезда критерию отбора, определение цвета вывода точки в операторе case. Далее происходит преобразование координат в галактические, затем в декартовы координаты проекции и в экранные координаты. Для простоты изложения мы ставим точку процедурой PutPixel, но можно нарисовать и другую геометрическую фигуру (ромб, круг).
Листинг 4.4. Построение распределения звезд по небесной сфере
Program Picture;
Uses Graph, HipMain, Projection;
{ В модуль Projection собраны все предыдущие подпрограммы }
var s : THipparcos;
driver,mode : integer; { Для инициализации графич. режима }
color : integer; { Цвет точки }
l, b : double; { Галактические координаты }
x, y : double; { Декартовы координаты }
u, v : integer; { Экранные координаты }
CX, CY : integer;{ Экранные координаты центра проекции }
SC : integer;{Масштаб перевода декартовых коорд. в экранные}
begin
{ Инициализация графического режима }
Driver:=detect; Mode:=0; InitGraph(Driver,Mode,'D:/BP/BGI');
{ Задание масштаба и центра }
{ Проекция Айтофа имеет X в диапазоне от -2 до 2, и зазор }
SC:=GetMaxX div 4 -10;
CX:=GetMaxX div 2; CY:=GetMaxY div 2;
AitoffGrid(30,CX,CY,SC,True); { Вывод сетки координат }
OpenHipparcosMain; { Открытие каталога и }
InitCriteria('I-II.txt'); { инициализация критерия }
while ReadHipparcosMain(s) do { Цикл чтения звезд }
if inCelestia(s.HIP) then { Проверка критерия }
begin
case s.SP[0] of { Определение цвета звезды }
'O','B': color:=LightBlue;
'A' : color:=LightCyan;
'F','G': color:=Yellow;
'K','M': color:=LightRed;
else color:=LightGray;
end; { case }
{ Перевод экваториальных координат в радианы, а затем
в галактические координаты }
Galaxy(rad(s.RADeg),rad(s.DEDeg),l,b);
{ Вычисление декартовых координат проекции Айтофа }
Aitoff(l,b,x,y);
Screen(x,y,CX,CY,SC,u,v); { Перевод в экранные координаты }
PutPixel(u,v,color);{Поставить точку (можно заменить на круг)}
end; { if и while }
ClearCriteria;
CloseHipparcosMain;
end.
4.2. Распределение звезд в пространстве
Знание параллаксов дает возможность получить все три пространственных координаты звезды каталога Hipparcos. С помощью несложных программ можно построить визуализацию заданной выборки звезды в пространстве.
Например, построим распределение в пространстве звезд спектральных классов
O-B5, которые находятся к нам ближе 500 пк и имеют относительную точность
определения параллакса лучше, чем 50%. Листинг 4.5 формирует текстовый
файл, где в три колонки идут прямоугольные галактические координаты звезд
, , 
.
Хотя задачу визуализации такого массива можно реализовать и самостоятельно,
но для решения подобного рода задач существует большое число математических
программ. Мы воспользуемся популярной и достаточно простой в освоении
программой MathCAD (годится любая версия старше 6.0). Вид экрана программы
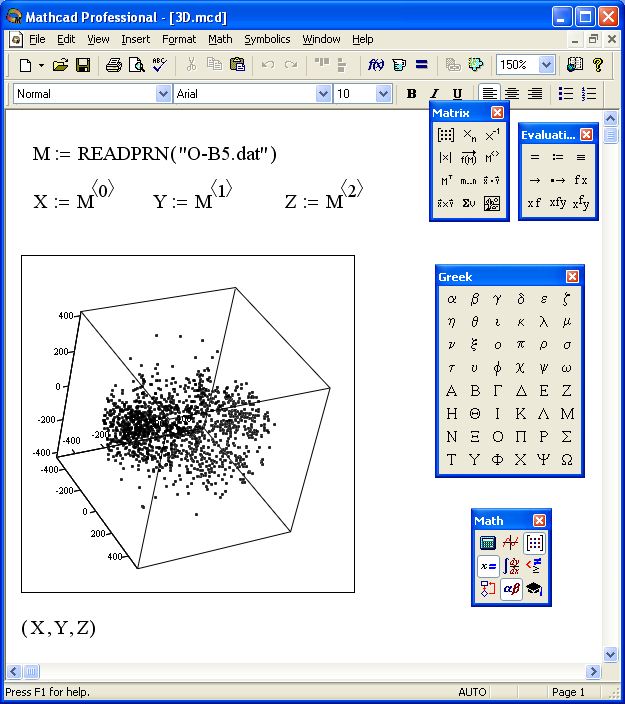
MathCAD вместе с текстом построения точечного графика представлен на
рис. 4.4. Первый оператор M:=READPRN(?O-B5.DAT?) считывает в матрицу M
содержимое файла, сформированного нашей программой. Последующие три
оператора задают три вектора, которые являются столбцами этой матрицы. Далее
с помощью команды меню Insert-Graph-3D Scatter Plot мы строим необходимую картину распределения звезд в
пространстве, с которой можно производить разные операции: вращение,
изменение масштаба, перспективы, добавление "тумана" и пр.
Листинг 4.5. Формирование прямоугольных координат звезд
Program Plot3D;
Uses HipMain,Projection;
Const Criteria = 'O-B5'; { Имя
файла критерия }
n : integer = 0; { Счетчик }
var s : THipparcos;
r : double; { Расстояние }
l, b : double; { Галактические
координаты }
x,y,z : double; { Декартовы галактические
координаты }
f : text; { Файл вывода результатов
}
begin
{ Выходной файл имеет расширение .DAT
}
assign(f,Criteria+'.DAT'); Rewrite(f);
OpenHipparcosMain;
{ Файл списка звезд имеет расширение
.TXT }
writeln(InitCriteria(Criteria+'.txt'),' звезд в критерии.');
while ReadHipparcosMain(s) do
begin
{ нет данных о параллаксе }
if (s.info and NoPlx)<>0
then continue;
{ "плохое" значение параллакса }
if s.plx<=0.0 then
continue;
{ низкая точность параллакса }
if s.sigma.plx/s.plx>0.5
then continue;
if inCelestia(s.HIP) then
begin
r:=1000.0/s.plx; { Вычисление расстояния в
пк }
if r>500.0 then continue; { Отброс далеких звезд
}
{ Перевод в галактические координаты
}
Galaxy(rad(s.RADeg),rad(s.DEDeg),l,b);
x:=r*cos(b)*cos(l); { Вычисление
прямоугольных }
y:=r*cos(b)*sin(l); { галактических
координат }
z:=r*sin(b);
writeln(f,x:10:2,y:10:2,z:10:2); { Вывод в
файл }
inc(n); { Увеличение счетчика на
единицу }
end; { if }
end; { while }
ClearCriteria;
CloseHipparcosMain;
Close(f);
writeln(n,' звезд обработано.');
end.
<< 3. Работа с ASCII | Оглавление | 5. Диаграмма Герцшпрунга-Рессела >>
|
Публикации с ключевыми словами:
астрометрия - каталоги - Hipparcos
Публикации со словами: астрометрия - каталоги - Hipparcos | |
См. также:
Все публикации на ту же тему >> | |
