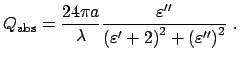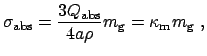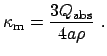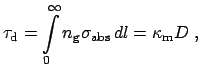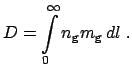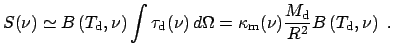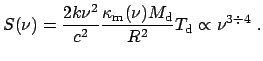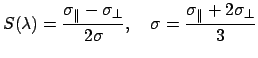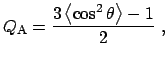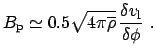<< 1. Введение | Оглавление | 3. Технические средства >>
2. Теория
Анализ взаимодействия электромагнитного излучения с пылинками
основан на теории рассеяния света малыми частицами. Поскольку в
интересующем нас диапазоне длина волны
(размера
частиц, 
мкм), ниже мы рассмотрим только этот предел.
Отметим, что вопросам интерпретации излучения пыли посвящено
довольно много работ. Одна из первых и наиболее часто
цитируемых - статья [1]. Эти вопросы рассмотрены
также в работе [2].
Из закона Кирхгофа излучательная способность среды связана с
коэффициентом поглощения. Поэтому рассмотрим прежде всего
характеристики поглощения излучения пылинками. В общем случае
полная величина ослабления интенсивности излучения пылью
складывается из истинного поглощения и рассеяния. Теория
показывает, что на волнах
мкм сечение рассеяния
много меньше сечения поглощения,
, причем с
увеличением длины волны относительный вклад рассеяния быстро
падает, поскольку
. Поэтому в дальнейшем мы будем
рассматривать только истинное поглощение.
Сечение поглощения пылинки можно записать в виде
где
- фактор эффективности поглощения,
который для сферических пылинок равен
Здесь
и
- действительная и
мнимая части диэлектрической проницаемости вещества пылинок
соответственно. Отсюда видно, что отношение
определяется только свойствами вещества пылинки и не зависит от ее
размера. Поэтому мы можем записать
где
- плотность вещества пылинки,
-
масса пылинки, а
- коэффициент поглощения
на единицу массы:
Таким образом, коэффициент поглощения пыли определяется ее массой в единичном объеме. Для оптической толщины пылевого облака получим [2]
где
- концентрация пылинок, а 
- масса пыли
в столбе единичного сечения:
В формулах (5), (6) пылинки считались одинаковыми, но это не принципиально. Можно было бы ввести интегрирование по размеру, конечный результат - то, что оптическая толща определяется массой пыли на луче зрения, - от этого не зависит.
Коэффициент поглощения пыли
зависит, однако,
от частоты. Обычно эта зависимость описывается степенным законом,
, с показателем
. Определение показателя 
из наблюдений задача
непростая, поскольку нужно учитывать, в частности,
неизотермичность пыли. В субмиллиметровом диапазоне теория и
большая часть наблюдательных оценок дают значения, близкие к
(например, [3]).
Что касается абсолютных значений показателя поглощения, то здесь
тоже имеется заметная неопределенность. Теоретические оценки для
пылинок разного типа отличаются на порядки. Определение
коэффициента поглощения из наблюдений основано обычно на оценках
количества пыли на луче зрения из оптических данных. В последнее
время наиболее приемлемыми считаются значения коэффициента
поглощения, полученные в работах [3] и (для плотных
облаков) [4]. Характерная величина
см
/г.
Перейдем теперь к излучению пыли. Наблюдаемая интенсивность
излучения оптически тонкого изотермичного пылевого облака с
температурой
будет равна [2]
где
- температура фонового излучения (2.7 К).
Плотность потока от такого облака, находящегося на расстоянии 
,
при
равна
Здесь
- полная масса пыли в облаке. В области
частот, где справедливо приближение Рэлея-Джинса,
Формулы (7) - (9) можно использовать для оценки столбцовой плотности и массы пыли в источнике, а поскольку отношение массы пыли к массе газа более или менее постоянно (
), - то и полной массы. Стоит отметить, однако, что
неизотермичность пыли может существенно повлиять на эти оценки
[5].
Важное значение имеет анализ радиального распределения
интенсивности излучения пыли в звездообразующих конденсациях,
поскольку это распределение несет информацию о радиальных профилях
плотности газа. Нетрудно показать [2], что если в
сферически-симметричном облаке плотность пыли (и газа) меняется по
закону
, а температура
(
- радиус), то в пределе (для бесконечного
облака) поверхностная яркость зависит от прицельного параметра
, как
. Краевые
эффекты приводят к некоторым поправкам, которые обсуждались,
например, в [6].
Остановимся теперь на вопросе о поляризации излучения пыли. Достаточно очевидно, что излучение ансамбля ориентированных несферических пылинок будет линейно поляризовано. Для степени поляризации можно получить выражение [2]
где
- угол между направлением распространения и осью
ориентации,
,
- сечения поглощения для
случаев, когда вектор 
параллелен и перпендикулярен оси
симметрии пылинки соответственно; 
- угол между осью
симметрии пылинки
и осью ориентации.
Параметр
характеризует степень ориентации пылинок.
Вопрос о механизме ориентации пылинок в плотных облаках (да и вообще в межзвездной среде) пока является дискуссионным. Возможны различные механизмы ориентации пылинок. Однако в конечном счете осью ориентации практически всегда является направление магнитного поля, поскольку время прецессии в магнитном поле меньше других характерных времен (пылинки обладают небольшим магнитным моментом вследствие наличия электрического заряда и пр.). Таким образом, исследования поляризации позволяют изучать структуру магнитного поля.
Для оценки напряженности магнитного поля по данным поляризационных
измерений часто используется формула Чандрасекара-Ферми, которая
связывает среднеквадратичное отклонение позиционного угла
поляризации
со среднеквадратичным отклонением
скорости газа вдоль луча зрения
(то есть с
шириной линии) и с альвеновской скоростью
, которая
зависит от магнитного поля 
(
,
где - плотность газа). В результате для оценки проекции
магнитного поля на картинную плоскость получается выражение
(например, [7])
Здесь 0.5 - эмпирический коэффициент.
Наконец, отметим, что, как показано в работах [8,9], пылинки могут заметно излучать на сантиметровых волнах (за счет электродипольного механизма при вращении небольших пылинок, а также за счет флуктуаций намагниченности пылинок). Этим может объясняться недавно обнаруженное избыточное излучение Галактики в этом диапазоне, коррелирующее с тепловым излучением пыли.
<< 1. Введение | Оглавление | 3. Технические средства >>
|
Публикации с ключевыми словами:
Межзвездная пыль - излучение
Публикации со словами: Межзвездная пыль - излучение | |
См. также:
Все публикации на ту же тему >> | |
