A.1 Матричная алгебра
Матрицей ![]() размера
размера ![]() называется таблица скалярных
величин:
называется таблица скалярных
величин:
![$\displaystyle A=
\begin{pmatrix}
a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & \cdots & \vdots \\ a_{m1} & a_{m2} & \cdots & a_{mn}
\end{pmatrix} \equiv [a_{ij}],
$](https://images.astronet.ru/pubd/2003/06/11/0001190894/tex/formula931.gif)
Для матриц определены следующие операции:
- Матрицы
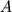 и
и 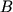 размера
размера 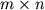 равны
равны 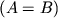 , если
для всех
, если
для всех 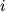 и
и 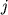 равны их элементы:
равны их элементы:
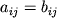 .
.
- Сумма матриц
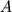 и
и 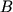 размера
размера 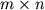 есть матрица
есть матрица
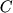 размера
размера 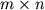 :
:
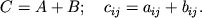
- Произведение матрицы
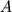 размера
размера 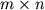 на скаляр
на скаляр 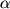 есть матрица
есть матрица 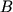 размера
размера 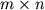 :
:
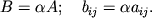
- Произведение матрицы
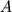 размера
размера 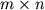 на матрицу
на матрицу 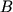 размера
размера 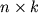 есть матрица
есть матрица 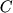 размера
размера 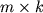 :
:
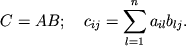
Матрица ![]() , транспонированная по отношению к матрице
, транспонированная по отношению к матрице ![]() размера
размера ![]() , есть матрица
, есть матрица
![]() размера
размера
![]() . Справедливы следующие соотношения:
. Справедливы следующие соотношения:
Матрица ![]() размера
размера ![]() называется квадратной матрицей
порядка
называется квадратной матрицей
порядка ![]() .
.
Квадратная матрица ![]() называется диагональной, если все
недиагональные элементы
называется диагональной, если все
недиагональные элементы ![]()
![]() равны нулю.
равны нулю.
Диагональная матрица ![]() размера
размера ![]() называется
единичной:
называется
единичной: ![]() , если все диагональные элементы равны единице:
, если все диагональные элементы равны единице:
![]() ,
, ![]() при
при ![]() . Если
. Если ![]() -- единичная
матрица размера
-- единичная
матрица размера ![]() , то для любой матрицы
, то для любой матрицы ![]() размера
размера
![]() справедливы равенства
справедливы равенства ![]() .
.
Квадратная матрица ![]() называется симметрической, если
называется симметрической, если ![]() ,
т.е. если
,
т.е. если
![]() .
.
Квадратная матрица ![]() называется невырожденной, если она имеет
единственную обратную матрицу
называется невырожденной, если она имеет
единственную обратную матрицу ![]() , определяемую условием:
, определяемую условием:
![]() .
.
Квадратная матрица ![]() называется ортогональной, если
называется ортогональной, если
![]() , т.е. если
, т.е. если
![]() .
.
Если квадратные матрицы ![]() и
и ![]() одного порядка невырождены,
скаляр
одного порядка невырождены,
скаляр
![]() , то
, то
Квадратная матрица не вырождена тогда и только тогда, когда ее строки (столбцы) линейно независимы.
<< A. Основные математические определения | Оглавление | A.2 Линейная алгебра >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |