3.7. Восход и заход небесных тел
В момент восхода и захода небесного тела его зенитное расстояние
![]() . Тогда формулу (3.1) можно преобразовать к виду:
. Тогда формулу (3.1) можно преобразовать к виду:
Зная склонение
Возможны три случая.
- Каждое из уравнений (3.25), (3.26) имеет два решения
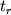 ,
,
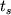 : значение
: значение 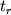 лежит между
лежит между 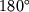 и
и 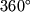 -- в
этот момент небесное тело восходит; значение
-- в
этот момент небесное тело восходит; значение 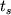 лежит между
лежит между
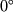 и
и 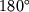 и является моментом захода. Это означает,
что небесное тело периодически восходит и заходит.
и является моментом захода. Это означает,
что небесное тело периодически восходит и заходит.
Азимут в точках восхода и захода определяется из системы уравнений:
где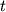 равняется
равняется 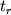 или
или 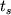 . Азимут в точке восхода может
принимать значения
. Азимут в точке восхода может
принимать значения
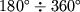 , в точке захода --
, в точке захода --
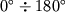 .
.
Чтобы найти время восхода (захода), необходимо к часовому углу
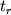 (или
(или 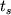 ) прибавить прямое восхождение
) прибавить прямое восхождение 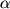 небесного
тела:
где
небесного
тела:
где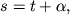
 -- местное звездное время. Определение звездного времени
будет дано ниже (см. §
5.2).
-- местное звездное время. Определение звездного времени
будет дано ниже (см. §
5.2).
- Если уравнения (3.25), (3.26) имеют одно решение, то это
означает, что небесное тело касается горизонта. Если это событие
происходит во время нижней кульминации, то
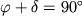 . При этом из (3.26) получим:
. При этом из (3.26) получим:
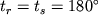 , а из (3.27)
, а из (3.27)
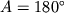 . Если небесное
тело достигает плоскости горизонта во время верхней кульминации,
то
. Если небесное
тело достигает плоскости горизонта во время верхней кульминации,
то
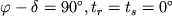 ,
, 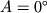 .
.
- Если правая часть уравнения (3.25) больше 1 или меньше -1, то
уравнение не имеет решений, т.е. восход и заход невозможны. Чтобы
решить вопрос, является ли небесное тело незаходящим или
невосходящим в северном полушарии, надо проверить неравенства:
В первом случае тело является незаходящим, во втором -- невосходящим.
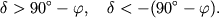
Заметим в конце параграфа, что при выводе формулы (3.25) не учитывалось явление рефракции (§6.1), которое приводит к подъему светила над горизонтом относительно его истинного положения. В результате рефракции время восхода наступает на несколько минут раньше, а время захода -- на несколько минут позже вычисленного по формулам (3.25), (3.26).
<< 3.6. Суточное вращение небесной | Оглавление | 3.8. Определение систем координат >>
|
Публикации с ключевыми словами:
астрометрия - сферическая астрономия - системы координат - шкалы времени
Публикации со словами: астрометрия - сферическая астрономия - системы координат - шкалы времени | |
См. также:
Все публикации на ту же тему >> | |
Мнения читателей [13]
Астрометрия
-
Астрономические инструменты
-
Астрономическое образование
-
Астрофизика
-
История астрономии
-
Космонавтика, исследование космоса
-
Любительская астрономия
-
Планеты и Солнечная система
-
Солнце