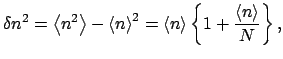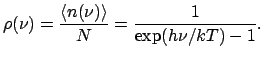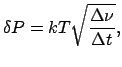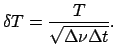<< Введение Современные миллиметровые и субмиллиметровые >>
Предел чувствительности
радиоастрономических приемников
В радиоастрономии как полезный сигнал, так и шум представляют собой стохастические процессы, каждый из которых может рассматриваться как "белый шум". Оптимальный алгоритм обнаружения в данном случае - это измерение энергии процесса
и сравнение ее с некоторым пороговым значением [1]. Приемное
устройство, реализующее эту процедуру, может быть названо энергетическим приемником. В радиоастрономии такой приемник называется радиометром.
Чувствительность радиометров определяется в идеале внешним фоном и соответственно флуктуациями числа фотонов на входе приемника. Дисперсия числа фотонов дается выражением
где
В равновесном случае при температуре ![]() среднее число фотонов в
одной моде поля дается распределением Планка:
среднее число фотонов в
одной моде поля дается распределением Планка:
Используя эти выражения, можно получить, что чувствительность
приемника по числу фотонов за время ![]() равна
равна
где
При
![]()
а поскольку
Выражение (7) является наиболее употребительным в
радиоастрономии для оценки чувствительности приемных систем.
Параметр ![]() называется шумовой температурой. Заметим, что
величина
называется шумовой температурой. Заметим, что
величина
![]() представляет собой, по существу,
число независимых колебаний в принимаемом излучении и изменение
дисперсии с ростом этой величины является обычным следствием
статистического усреднения.
представляет собой, по существу,
число независимых колебаний в принимаемом излучении и изменение
дисперсии с ростом этой величины является обычным следствием
статистического усреднения.
Выше мы предполагали, что приемник не вносит дополнительных шумов
и чувствительность определяется исключительно флуктуациями фона и
исследуемого излучения. Однако практически всегда (по крайней мере
на миллиметровых и субмиллиметровых волнах) шумы приемной
аппаратуры являются основным фактором, ограничивающим
чувствительность. Вклад шумов приемника обычно можно описать как
добавку к шумовой температуре. Полная шумовая температура,
называемая шумовой температурой системы
![]() ,
складывается, таким образом, из температуры фона и шумовой
температуры приемника:
,
складывается, таким образом, из температуры фона и шумовой
температуры приемника:
Стоит отметить, что с точки зрения повышения чувствительности снижение шумовой температуры в 2 раза эквивалентно уменьшению времени накопления в 4 раза. Понятно, что разработка приемных систем с возможно более низким уровнем собственных шумов была и остается важнейшей технической задачей радиоастрономии. И хотя благодаря прогрессу технологии шумовые параметры приемников постоянно улучшаются, существует фундаментальный предел снижения шумовой температуры (называемый "квантовым пределом"), который следует из соотношения неопределенностей. В частности, предельная точность измерений энергии определяется соотношением неопределенностей энергия-время:
Учитывая, что
В большинстве случаев на входе радиоастрономических приемников
используется некий вариант линейного "когерентного"
преобразователя, т. е. устройства, которое линейным образом
преобразует входной сигнал, причем сдвиг фазы входного сигнала
приводит к такому же (или противоположному по знаку) сдвигу фазы
выходного сигнала. Это может быть усилитель или смеситель,
изменяющий частоту сигнала. Так, в миллиметровом и
субмиллиметровом диапазонах наиболее распространенным типом
приемника является супергетеродинный радиометр со смесителем на
входе. Мы будем называть это устройство усилителем и
характеризовать его коэффициентом усиления по числу квантов:
![]() , где
, где ![]() и
и ![]() - число фотонов на входе и выходе
соответственно. Кстати, для радиоастрономических смесителей,
которые преобразуют частоту вниз на несколько порядков,
- число фотонов на входе и выходе
соответственно. Кстати, для радиоастрономических смесителей,
которые преобразуют частоту вниз на несколько порядков,
![]() (
(![]() - потери преобразования по
мощности).
- потери преобразования по
мощности).
Соотношение неопределенностей (10) применимо как
ко входу, так и к выходу усилителя. И если мы предположим, что
усилитель (![]() ) не вносит собственных шумов в преобразуемый
сигнал, то есть
) не вносит собственных шумов в преобразуемый
сигнал, то есть
![]() , то
немедленно придем к противоречию, так как в этом случае
, то
немедленно придем к противоречию, так как в этом случае
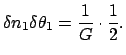
Таким образом, усилитель обязательно должен добавлять некоторый
шум к входному сигналу. Анализ показывает (см., например,
[2]), что минимальная шумовая температура усилителя
(при ![]() ) составляет
) составляет
![]() . Это и есть "квантовый
предел" шумовой температуры.
. Это и есть "квантовый
предел" шумовой температуры.
<< Введение Современные миллиметровые и субмиллиметровые >>
|
Публикации с ключевыми словами:
астрономические инструменты - Приборостроение
Публикации со словами: астрономические инструменты - Приборостроение | |
См. также:
Все публикации на ту же тему >> | |