|
Штарка эффект
- расщепление и сдвиг уровней энергии атомов и молекул под дейстивем электрич. поля. Обнаруживается по расщеплению и сдвигу линий в спектах испускания и поглощения.Открыт немецким физиком Й. Штарком в 1913 г. при изучении спектра водорода. Кроме водорода Ш.э. подробно изучен в спектрах гелия, щелочных металлов (Li, Na, K и т.д.) и ряда др. элементов.
Ш.э. был объяснен на основе квантовой механики. Квантовая система (атом, молекула)
в состоянии с определенной энергией ![]() приобретает во внеш.
электрич.
поле E дополнительную энергию
приобретает во внеш.
электрич.
поле E дополнительную энергию ![]() (т.к.
электрич. поле изменяет состояние входящих в систему заряженных частиц, напр., электронов
в атоме). В результате уровень энергии, к-рому соответствует одно возможное состояние
атома (невырожденный уровень), в электрич. поле будет иметь энергию
(т.к.
электрич. поле изменяет состояние входящих в систему заряженных частиц, напр., электронов
в атоме). В результате уровень энергии, к-рому соответствует одно возможное состояние
атома (невырожденный уровень), в электрич. поле будет иметь энергию ![]() ,
т.е. он сместится. Для вырожденного уровеня энергии (ему соответствует неск. возможных
состояний системы с одинаковой энергией
,
т.е. он сместится. Для вырожденного уровеня энергии (ему соответствует неск. возможных
состояний системы с одинаковой энергией ![]() ) различные состояния
могут приобрести разные дополнительные энергии
) различные состояния
могут приобрести разные дополнительные энергии ![]() 1,
2, ...,g, где g - степень вырождения уровня). В результате вырожденный
уровень расщепляется на подуровни с энергией
1,
2, ...,g, где g - степень вырождения уровня). В результате вырожденный
уровень расщепляется на подуровни с энергией ![]() ,
число к-рых равно числу различных значений
,
число к-рых равно числу различных значений ![]() . Так, уровень
энергии атома с заданным значением момента количества движения
. Так, уровень
энергии атома с заданным значением момента количества движения ![]() (J=0, 1, 2... - квантовое число) расщепляется в электрич. поле на
подуровни, характеризуемые различными значениями др. квантового числа m (различной
величиной проекции момента M на направление электрического поля). Однако значениям
-m и +m соответствует одинаковая дополнительная энергия
(J=0, 1, 2... - квантовое число) расщепляется в электрич. поле на
подуровни, характеризуемые различными значениями др. квантового числа m (различной
величиной проекции момента M на направление электрического поля). Однако значениям
-m и +m соответствует одинаковая дополнительная энергия ![]() ,
так что все штарковские подуровни (с
,
так что все штарковские подуровни (с ![]() ) оказываются дважды
вырожденными (в отличие от расщепления в магнитном поле, где все подуровни не вырождены,
см. Зеемана эффект).
) оказываются дважды
вырожденными (в отличие от расщепления в магнитном поле, где все подуровни не вырождены,
см. Зеемана эффект).
|
|
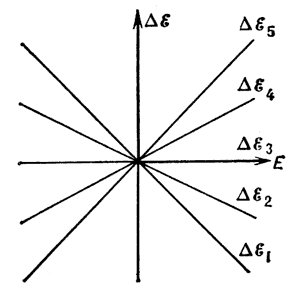
Рис. 1. Зависимость величины расщепления от напряженности электрического поля E при линейном эффекте Штарка (расщепление уровня атома водорода, которому соответствует главное квантовое число n=3, на 5 подуровней). |
Различают линейный Ш.э., когда ![]() пропорционально E
(рис. 1), и квадратичный Ш.э., когда
пропорционально E
(рис. 1), и квадратичный Ш.э., когда ![]() пропорционально
E2 (рис. 2). В первом случае картина расщепления
уровней энергии и получающихся при переходах между ними спектр. линий симметрична,
во втором
- несимметрична. Линейный Ш.э. характерен для водорода в не слишком сильных полях
(в полях ~ 104 В/см он составляет тысячные доли эВ). Уровень
энергии
атома водорода с заданным значением главного квантового числа n симметрично
расщепляется на 2n-1 равноотстоящих подуровней (рис. 1 соответствует n=3,
2n-1=5). У компонентов спектр. линии, обусловленных переходами между расщепленными
в электрич. поле уровнями, наблюдается эффект поляризации (см. Поляризация
электромагнитного излучения). Если электрич. поле ориентировано перпендикулярно к
наблюдателю, то часть компонентов поляризована продольно (
пропорционально
E2 (рис. 2). В первом случае картина расщепления
уровней энергии и получающихся при переходах между ними спектр. линий симметрична,
во втором
- несимметрична. Линейный Ш.э. характерен для водорода в не слишком сильных полях
(в полях ~ 104 В/см он составляет тысячные доли эВ). Уровень
энергии
атома водорода с заданным значением главного квантового числа n симметрично
расщепляется на 2n-1 равноотстоящих подуровней (рис. 1 соответствует n=3,
2n-1=5). У компонентов спектр. линии, обусловленных переходами между расщепленными
в электрич. поле уровнями, наблюдается эффект поляризации (см. Поляризация
электромагнитного излучения). Если электрич. поле ориентировано перпендикулярно к
наблюдателю, то часть компонентов поляризована продольно (![]() -компоненты),
остальные
- поперечно (
-компоненты),
остальные
- поперечно (![]() -компоненты). При продольном направлении поля
-компоненты). При продольном направлении поля ![]() -компоненты
не появляются, а на месте
-компоненты
не появляются, а на месте ![]() -компонентов возникают
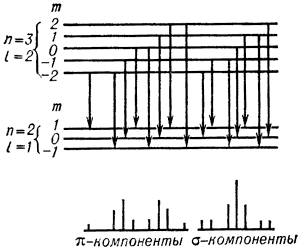
неполяризованные компоненты. Интенсивности разных компонентов различны. На рис. 3
показано расщепление в результате Ш.э. спектр. линии водорода H
-компонентов возникают
неполяризованные компоненты. Интенсивности разных компонентов различны. На рис. 3
показано расщепление в результате Ш.э. спектр. линии водорода H![]() .
.
|
|
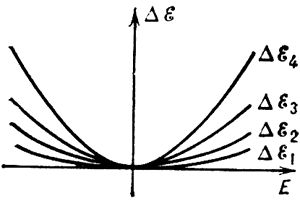
Рис. 2. Зависимость величины расщепления от напряженности электрического поля E при квадратичном эффекте Штарка (подуровни оказываются отстоящими на разные расстояния). |
Кроме водорода линейный Ш.э. наблюдается в водородоподобных атомах (He+, Li2+, B3+ и т.д.) и для сильно возбужденных уровней др. атомомв (в ряде случаев Ш.э. приводит к появлению запрещенных спектральных линий).
В сильных полях, а также в слабых полях для ряда элементов имеет место главным образом квадратичный Ш.э. с асимметричной картиной расщепления. Величина квадратичного эффекта невелика (в полях ~ 105 В/см расщепление достигает десятитысячных долей эВ).
|
|
Рис. 3. Расщепление линии водорода H в электрическом поле. Различно поляризованы компоненты линии ( комбинациях подуровней. |
Ш.э. наблюдается не только в постоянных, но и в переменных электрич. полях. Влияние высокочастотного электрич. поля на уровни энергии атомов (ионов) определяет, в частности, уширение спектральных линий космич. плазмы. Движение частиц плазмы и связанное с этим изменение расстояний между ними приводят к быстрым изменениям электрич. поля около каждой излучающей частицы. В результате энергетич. уровни атомов (ионов), расщепляясь, смещаются на неодинаковую величину. Для излучения совокупности таких частиц характерно увеличение ширины спектр. линий (т.н. штарковское уширение линий). Ш.э. позволяет оценить концентрацию заряженных частиц в космич. плазме (напр., в атмосферах звезд).
Лит.:
Ельяшевич М.А., Атомная и молекулярная спектроскопия, М., 1962; Мустель Э.Р., Звездные
атмосферы, М., 1960.
(М.А. Ельяшевич)
М. А. Ельяшевич, "Физика Космоса", 1986
Глоссарий Astronet.ru
|
Публикации с ключевыми словами:
эффект Штарка
Публикации со словами: эффект Штарка |

|
|
См. также:
| |