Астронет > Механика сплошных сред

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Механика сплошных сред

Устойчивость упругого равновесия

Зная упругие свойства тел, мы всегда можем рассчитать деформации под действием заданных сил. Такие расчеты проводятся в курсе теоретической физики, Их основная идея сводится к следующему.

Рис. 1.19.

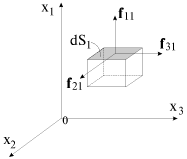
Под действием внешних сил в теле создаются напряжения. Эти напряжения действуют на элементарный объем через поверхности, его ограничивающие. На рис. 1.19 изображена одна нормальная f₁₁ и две тангенциальные силы f₂₁ и f₃₁, действующие на заштрихованную грань кубика. Модули этих сил равны

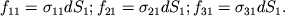
$f_{11}=\sigma_{11}dS_1 ; f_{21}=\sigma_{21}dS_1 ; f_{31}=\sigma_{31}dS_1.$

(1.56)

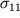
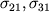
Здесь индексы указывают на то, что силы приложены к площадке, перпендикулярной x₁ и действуют в направлении оси x₁ ( $\sigma_{11}$ - нормальное напряжение) и осей x₂ и x₃ ( $\sigma_{21},\sigma_{31}$ - соответствующие тангенциальные напряжения) Аналогично, но с другими индексами, записываются модули сил, приложенных к площадкам dS₂ и dS₃. Полная сила, действующая на выделенный объем, зависит как от ориентации площадок, ограничивающих этот объем, так и от внутренних напряжений в той области, где находится рассматриваемый объем. 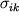Эти напряжения описываются совокупностью девяти величин $\sigma_{ik}$ (i, k=1,2,3), которые составляют тензор напряжений. В упругих телах деформации пропорциональны соответствующим напряжениям. Таким образом, сложные деформации упругих тел описываются системой линейных дифференциальных уравнений, связывающих компоненты тензора деформаций и тензора напряжений. 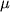Материальные свойства сред представлены, как правило, коэффициентом Пуассона $\mu$ (1.4) и модулем всестороннего сжатия k (1.29). Анализ такой системы уравнений позволяет не только рассчитать деформацию тел, но и ответить на вопрос, устойчивы ли эти деформации или нет.

Рис. 1.20.

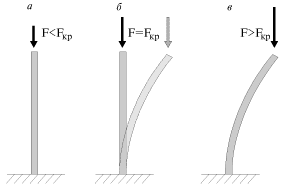
В качестве примера рассмотрим задачу о потере устойчивости стержня при его продольном сжатии силой F (рис. 1.20). При малых сжимающих силах сжатия стойка находится в устойчивом равновесии, т.к., испытав малое случайное отклонение от вертикали, стойка, тем не менее, возвращается в вертикальное положение. С увеличением нагрузки случайные отклонения исчезают все медленнее со временем. При F=F_кр наступает состояние безразличного равновесия: прямолинейная форма теряет устойчивость, а устойчивым уже будет изогнутое состояние стержня (пунктир на рис. 1.20 б). Такое раздвоение равновесия, характеризующегося двумя его формами, называется бифуркацией. Новая криволинейная форма равновесия при F>F_кр хотя и устойчива, однако такая деформация мало приемлема, поскольку в стойке возникают недопустимо большие изгибы и напряжения. Задача о выпучивании стержня при продольном сжатии была решена в XVIII веке выдающимся математиком Леонардом Эйлером. 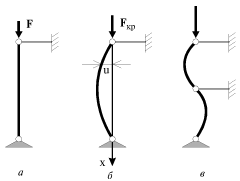Рассчитаем, следуя Эйлеру, значение критической силы F_кр и форму изогнутого стержня, когда последний шарнирно закреплен за оба конца (рис. 1.21).

Рис. 1.21.

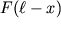
Форма изогнутого стержня u(x) может быть получена из уравнения (1.46), в котором вместо момента поперечной силы $F(\ell-x)$ для произвольного сечения x=const, отмеченного пунктиром, следует записать момент сдавливающей силы в виде M=Fu. Тогда уравнение (1.46) примет вид:

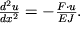
$\frac{d^2 u}{dx^2}=-\frac{F\cdot u}{EJ}.$

(1.57)

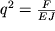
Если обозначить $q^2=\frac{F}{EJ}$ и обратить внимание, что уравнение (1.57) аналогично уравнению гармонических колебаний, то его решение записывается сразу в виде

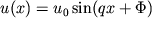
$u(x)=u_0 \sin(qx + \Phi)$

(1.58)

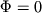
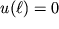
Из граничного условия u(0)=0 следует, что $\Phi=0$ . Из другого граничного условия $u(\ell)=0$ следует

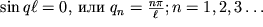
$\sin q\ell=0$, или $q_n=\frac{n\pi}{\ell}; n=1,2,3\ldots$

(1.59)

Каждому значению q_n соответствует своя конфигурация изогнутого стержня, представляющая собой синусоиду, имеющую n полуволн. Эти конфигурации возникают при соответствующих значениях сил, равных

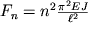
$F_n=n^2\frac{\pi^2 EJ}{\ell^2}$

(1.60)

При n=1 формула (1.60) дает значение критической силы

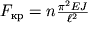
$F_{кр}=n\frac{\pi^2 EJ}{\ell^2}$

(1.61)

Последняя формула была получена Эйлером и носит его имя. Другие направленные формы равновесия (n=2, 3...) являются неустойчивыми, однако они могут быть реализованы, если стержень дополнительно закрепить шарнирными опорами в сечениях, где u=0 (рис.1.21в). Полученный результат имеет большое практическое значение. В силу неустойчивости стержней при их сжатии, толкающие рычаги и штоки в машинах делают по возможности короче и большого сечения, в то время как тянущие штоки, имеющие большой запас прочности на разрыв, могут быть и не очень толстыми. По аналогии легко понять, что герметичные емкости, испытывающие нагрузку на разрыв (например, паровые котлы) делают более тонкостенными, чем емкости, подверженные сжатию (оболочки батискафов, подводных лодок и пр.)

Энергия упругих деформаций

При деформации внешние силы совершают работу. Эта работа в общем случае идет на увеличение потенциальной энергии (нагревание тела). Так, например, если мы будем пытаться переломить проволоку, то место ее многократного изгиба может сильно нагреться, прежде чем проволока переломится. В реальных телах возникающие силы внутренних напряжений зависят не только от величины деформаций, но и от их скорости. Поэтому работа против таких сил, называемых силами "внутреннего трения" и идет на нагревание тела. С этими силами и связаны пластические деформации, когда не выполняется закон Гука и существуют остаточные деформации при прекращении внешнего воздействия.

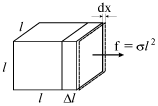Рис. 1.22.

Посчитаем работу, затрачиваемую на малую деформацию элемента объема тела. При растяжении предварительно уже деформированного кубика (рис.1.22) на величину dx элементарная работа

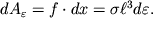
$dA_\varepsilon =f\cdot dx = \sigma\ell^3 d\varepsilon.$

(1.62)

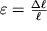
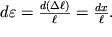
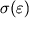
В (1.62) учтено, что $\varepsilon=\frac{\Delta \ell}{\ell}$ , а $d\varepsilon=\frac{d(\Delta\ell)}{\ell}=\frac{dx}{\ell}.$ Поскольку, как следует из рис. 1.7, $\sigma(\varepsilon)$ - нелинейная функция деформаций, то полная работа, затрачиваемая на приведение тела в деформационное состояние, равна

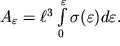
$A_\varepsilon= \ell^3 \int\limits_0^{\varepsilon} \sigma(\varepsilon) d\varepsilon.$

(1.63)

По аналогии, работа при сдвиге задается интегралом вида:

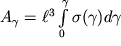
$A_\gamma= \ell^3 \int\limits_0^{\gamma} \sigma(\gamma) d\gamma$

(1.64)

Рис. 1.23.

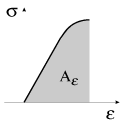
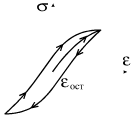
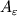
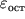
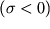
На диаграмме (1.23) работа $A_\varepsilon$ равна численно заштрихованной площади. Опыт, однако, показывает, что если деформации выйдут за область упругости, то при снятии внешних нагрузок в теле будут существовать остаточные деформации $\varepsilon_{ост}$ (рис. 1.24). Чтобы их устранить, надо приложить сжимающую силу $(\sigma<0)$ . Такое неоднозначное поведение деформации в зависимости от приложенных напряжений носит название упругого гистерезиса. 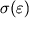При периодически повторяющихся деформациях диаграмма $\sigma(\varepsilon)$ изобразится замкнутой кривой, которая называется петлей гистерезиса. Площадь этой петли, очевидно, в соответствии с законом сохранения энергии, равна количеству тепла, идущего на нагревание тела. 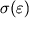Когда деформации не выходят за пределы линейного участка $\sigma(\varepsilon)$ , гистерезис отсутствует. 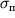На практике детали механизмов, испытывающие многократные, периодически повторяющиеся деформации, делают из материалов с большой величиной предела пропорциональности $\sigma_п$ . 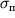Так, например, для закаленной пружинной стали, этот предел, как видно из таблицы, имеет очень высокую величину: $\sigma_п$ =7500 кг/см² .По этой причине, например, пружины клапанов двигателей делают из закаленной стали.

Рис. 1.24.

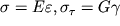
На линейном участке, где $\sigma=E \varepsilon , \sigma_\tau=G\gamma$ , интегралы (1.63) и (1.64) легко вычисляются:

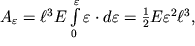
$A_\varepsilon=\ell^3 E \int\limits_0^\varepsilon \varepsilon \cdot d\varepsilon= \frac{1}{2} E \varepsilon^2 \ell^3,$

(1.65)

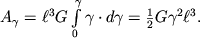
$A_\gamma=\ell^3 G \int\limits_0^\gamma \gamma \cdot d\gamma= \frac{1}{2} G \gamma^2 \ell^3.$

(1.66)

В этом случае работа затрачивается только на увеличение потенциальной энергии упругой деформации. В единице объема деформированного тела запасается энергия

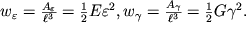
$w_\varepsilon=\frac{A_\varepsilon}{\ell^3}=\frac{1}{2} E \varepsilon^2, w_\gamma=\frac{A_\gamma}{\ell^3}=\frac{1}{2} G \gamma^2.$

(1.67)

Величины и носят название объемных плотностей энергии деформации растяжения и сдвига соответственно. Они играют определенную роль при подсчете количества энергии, переносимой акустической волной в сплошных средах.

Назад | Вперед

Публикации с ключевыми словами: механика - гидродинамика - газодинамика - упругость Публикации со словами: механика - гидродинамика - газодинамика - упругость
См. также: Д'Аламбера-Эйлера парадокс Механика твердого тела. Лекции. Число Маха Вариационные принципы механики Конус Маха Бернулли уравнение Баротропное явление Все публикации на ту же тему >>

Мнения читателей [4]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце