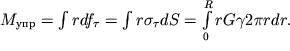Астронет > Механика сплошных сред

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Механика сплошных сред

Изгиб балок

Рис. 1.11.

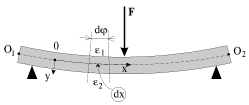
Балка, т.е. стержень, испытывающий изгиб, деформируется таким образом, что первоначально прямая ось балки О₁О₂ становится криволинейной; эта ось называется упругой линией (рис. 1.11). Рассмотрим изгиб балки под действием внешней силы F, пренебрегая ее весом. Все волокна, лежащие ниже этой линии, удлиняются (в них возникают растягивающие напряжения), а волокна, лежащие выше этой линии, сжимаются (в них возникают сжимающие напряжения). Между растянутыми волокнами находится нейтральный слой. 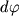При этом два, первоначально параллельные сечения и находящиеся на расстоянии dx друг от друга, при изгибе образуют некоторый угол $d\varphi$ . Для удобства описания распределения деформации и напряжений свяжем со стержнем систему координат с началом в некоторой точке О упругой линии О₁О₂ и осями x и y, направленными вдоль упругой линии и в поперечном сечении соответственно (см. рис. 1.11). 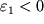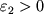Легко видеть, что деформации в некотором сечении x=const линейно нарастают вдоль оси y от $\varepsilon_1<0$ до $\varepsilon_2>0$ . Это дает основание в соответствии с законом Гука записать распределение напряжений в виде

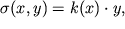
$\sigma(x,y)=k(x)\cdot y,$

(1.30)

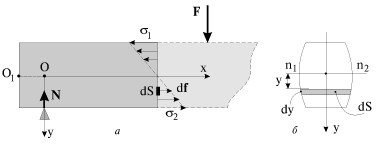
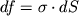
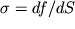
где k - неизвестный коэффициент пропорциональности, меняющийся, вообще говоря, от сечения к сечению. Распределение напряжений (1.30) в произвольном сечении стержня удобно изобразить графически, если в каждой точке сечения восстановить перпендикулярный к нему вектор, мысленно равный силе, действующей на площадку dS: $df=\sigma \cdot dS$ (рис.1.12а), т.е. $\sigma=df/dS$ .

Рис. 1.12.

Рассмотрим равновесие части балки, расположенной слева от сечения. Начало координат поместим в сечение, вдоль которого действует сила реакции опоры. Предположим, что балка имеет вертикальную плоскость симметрии, как это изображено на рис. 1.12 б, и внешние силы лежат в этой плоскости. Нейтральный слой пересекает сечение балки по прямой n₁n₂. Для равновесия этого куска балки необходимо, чтобы выполнялись следующие известные из статики условия. Во-первых сумма всех горизонтальных сил должна быть равна нулю, т.е.

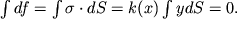
$\int df=\int \sigma\cdot dS= k(x)\int y dS=0.$

(1.31)

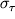
Поскольку интеграл (1.31) вычисляется в поперечном сечении балки, то понятно, что нейтральная ось n₁n₂, на которой лежит начало координат, должна проходить через центр масс поперечного сечения балки. Во-вторых, сумма всех вертикальных сил может быть равна нулю, если в сечении, кроме изображенных нормальных напряжений, будут действовать и касательные напряжения $\sigma_\tau$ , чтобы скомпенсировать силу реакции опоры N, т.е.

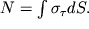
$N=\int \sigma_\tau dS.$

(1.32)

В большинстве случаев касательные напряжения при изгибе малы по сравнению с нормальными и при расчете балки на прочность не учитываются. В третьих, сумма моментов всех сил относительно любой точки должна быть равна нулю. Если в качестве такой точки выбрать центр масс рассматриваемого сечения, то это условие запишется в виде.

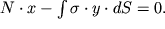
$N\cdot x -\int \sigma\cdot y \cdot dS = 0.$

(1.33)

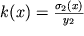
Если подставить сюда распределение напряжений (1.30), где коэффициент пропорциональности $k(x)=\frac{\sigma_2(x)}{y_2}$ (y₂ - расстояние между нейтральным слоем и наиболее растянутым нижним волокном), то мы приходим к условию

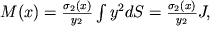
$M(x)=\frac{\sigma_2(x)}{y_2}\int y^2 dS = \frac{\sigma_2(x)}{y_2}J,$

(1.34)

где

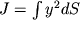
$J=\int y^2 dS$

(1.35)

момент инерции поперечного сечения относительно центральной оси n₁n₂, M(x)=N*x - момент силы реакции. Отношение J/y₂ зависит от размеров и формы сечения и называется осевым моментом сопротивления:

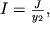
$I=\frac{J}{y_2},$

(1.36)

а уравнения (1.34) можно представить в виде

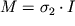
$M=\sigma_2\cdot I$

(1.37)

Рис. 1.13.

Для расчета прочности балок необходимо знать распределение напряжений , возникающих при известных моментах внешних сил, что может быть получено из (1.34) в виде

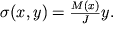
$\sigma(x,y)=\frac{M(x)}{J}y.$

(1.38)

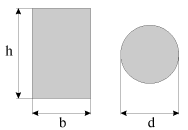
Моменты инерции поперечных сечений (прямоугольного и кругового) равны

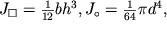
$J_{\Box}=\frac{1}{12} bh^3 , J_{\circ}=\frac{1}{64}\pi d^4 ,$

(1.39)

а соответствующие им осевые моменты сопротивления -

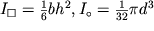
$I_{\Box}=\frac{1}{6} bh^2 , I_{\circ}=\frac{1}{32}\pi d^3$

(1.40)

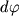
Из (1.37) следует, что прочность балок возрастает при увеличении осевого момента сопротивления, причем, как следует из (1.40), прочность балки прямоугольного сечения достигается эффективнее за счет увеличения ее высоты h. Полученные результаты позволяют рассчитать направление осевой линии балки. 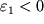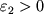Элементарный угол $d\varphi$ , на который повернулись сечения x и x+dx, очевидно, связан с двумя деформациями $\varepsilon_1<0$ и $\varepsilon_2>0$ крайних волокон соотношением

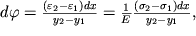
$d\varphi=\frac{(\varepsilon_2-\varepsilon_1)dx}{y_2-y_1}=\frac{1}{E}\frac{(\sigma_2-\sigma_1)dx}{y_2-y_1},$

(1.41)

где y₂-y₁- расстояние между крайними волокнами. Подставляя в (1.41) напряжение (1.38), получим

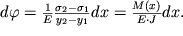
$d\varphi= \frac{1}{E}\frac{\sigma_2-\sigma_1}{y_2-y_1}dx=\frac{M(x)}{E\cdot J}dx.$

(1.42)

В частности, легко рассчитать изгиб невесомой горизонтальной балки, выступающей из стены (консольной балки) на расстояние $\ell$ , к концу которой приложена вертикальная сила F(рис.1.14). Как следует из (1.42), в произвольном сечении x

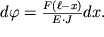
$d\varphi=\frac{F(\ell-x)}{E\cdot J}dx.$

(1.43)

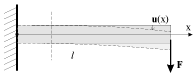Рис. 1.14.

Если ось балки в каждом сечении сместилась вниз на расстояние u(x), то, очевидно, угол наклона оси балки к горизонтальной оси в сечении x

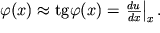
$\varphi(x)\approx {\rm tg} \varphi(x)= \left. \frac{du}{dx}\right|_x.$

(1.44а)

В сечении x+dx угол наклона несколько больше:

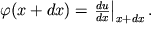
$\varphi (x+dx)= \left. \frac{du}{dx}\right|_{x+dx}.$

(1.44б)

Приращение этого угла

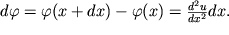
$d\varphi=\varphi(x+dx)-\varphi(x)=\frac{d^2 u}{dx^2}dx.$

(1.45)

Приравнивая правые части (1.45) и (1.43), получаем уравнение:

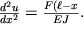
$\frac{d^2 u}{dx^2}=\frac{F(\ell-x}{EJ}.$

(1.46)

Интегрируя два раза при условии, что u(0)=0 (конец закреплен), получаем искомое искривление балки в виде

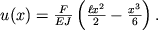
$u(x)=\frac{F}{EJ}\left( \frac{\ell x^2}{2}-\frac{x^3}{6}\right).$

(1.47)

В частности, смещение конца балки под действием силы F, называемое стрелой прогибы, оказывается равным

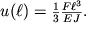
$u(\ell)=\frac{1}{3}\frac{F\ell^3}{EJ}.$

(1.48)

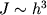
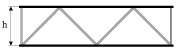
Если балка имеет прямоугольное сечение, то ее стрела прогиба очень быстро уменьшается по мере увеличения высоты балки h, поскольку $J\sim h^3$ . Для экономии материала иногда используют пустотелые балки. Такая балка значительно легче цельной, а ее осевой момент сопротивления (см. 1.36) остается достаточно большим. Для повышения жесткости используют конструкции, называемые фермами (рис. 1.15). Фермы - это достаточно легкие ажурные конструкции, высота которых, в сильной степени определяющая момент сопротивления, может достигать десятков метров.

Рис. 1.15.

Фермы - это достаточно легкие ажурные конструкции, высота которых, в сильной степени определяющая момент сопротивления, может достигать десятков метров. В качестве примера на рис. 1.16 показана типичная конструкция подвесного моста. Необходимая жесткость такого моста обеспечивается фермами, состоящими из жестких элементов и тросов. Рекордную длину 3910 метров имеет мост, соединяющий два острова в Японии. Длина его центрального пролета L составляет 1990 метров при высоте опор Н = 297 метров.

Рис. 1.16.

Кручение валов

Деформации сдвига возникают при скручивании валов машин и механизмов, когда посредством вала передается вращательное усилие от одной части механизма к другой. Если, например, нижнее основание вала, изготовленное в виде круглого стержня радиуса R и длины $\ell$ , закрепить, а к верхнему основанию приложить закручивающий момент внешних сил M, то вал деформируется. На рис. 1.17 изображены деформируемый вал и деформация сдвига элементарного объема. 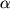Очевидно, что угол сдвига $\alpha$ зависит от удаления этого объема от оси вала. 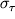Касательные напряжения $\sigma_\tau$ , ответственные за эти деформации, создают в сечении момент упругих сил, равный

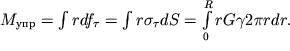
$M_{упр}= \int rdf_\tau=\int r\sigma_\tau dS= \int\limits_0^R rG\gamma 2\pi r dr.$

(1.49)

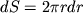
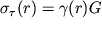
Здесь учтено, что площадь элементарного кольца радиуса r и толщиной dr равна: $dS=2\pi rdr$ , а $\sigma_\tau(r)=\gamma(r)G$ .

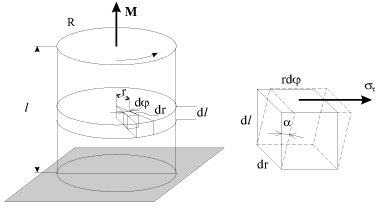Рис. 1.17.

Из условия равновесия части вала, находящегося, например, выше от рассматриваемого сечения, следует, что

M_упр=M

(1.50)

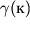
и M_упр не зависит от выбора сечения вала. Зависимость $\gamma(к)$ должна быть линейной функцией расстояния r, т.е.

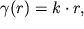
$\gamma(r)=k\cdot r,$

(1.51)

где неизвестный коэффициент пропорциональности k может быть определен из (1.49) при учете (1.50)

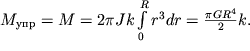
$M_{упр}=M=2\pi J k \int\limits_0^R r^3 dr = \frac{\pi G R^4}{2}k.$

(1.52)

Таким образом, сдвиговые деформации

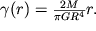
$\gamma(r)=\frac{2 M }{\pi G R^4 }r.$

(1.53)

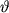
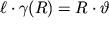
Они пропорциональны моменту внешних сил и обратно пропорциональны четвертой степени R. Из последнего соотношения легко посчитать угол кручения $\vartheta$ , на который повернется верхнее основание стержня относительно нижнего. Из очевидного равенства $\ell\cdot \gamma(R)=R\cdot \vartheta$ с учетом (1.53) находим

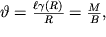
$\vartheta=\frac{\ell \gamma(R)}{R}=\frac{M}{B},$

(1.54)

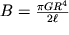
где $B=\frac{\pi G R^4}{2\ell}$ - модуль кручения, зависящий от размеров вала и модуля сдвига материала, из которого вал изготовлен. Для создания жестких валов необходимо увеличивать диаметр и сокращать длину. Для экономии материала валы часто делают пустотелыми, обеспечивая при этом высокую жесткость вала. В ряде случаев, наоборот, используют валы, изготовленные в виде тонких нитей, как, например, нити подвеса крутильных весов, используемых Кулоном в опытах по исследованию электростатического взаимодействия и П.Н.Лебедевым - в опытах по измерению давления света. В этих опытах тонкие кварцевые нити закручивались на значительные углы при действии ничтожно малых моментов сил, что, конечно, Обеспечивает высокую чувствительность крутильных весов. Отметим, что на практике часто различные строительные конструкции (балки, фермы и др.) должны обладать достаточной сопротивляемостью как к изгибу, так и кручению. Примером таких конструкций является железнодорожный рельс, балка двухтаврового сечения, швеллер и др.

Рис. 1.18.

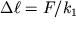
Интересно отметиить, что при растяжении пружин могут одновременно возникать деформации растяжения и сдвига. Пружины с малыми углами наклона витков к горизонтали (рис. 1.18) при их растяжении вдоль оси в отличие от стержней испытывают деформации сдвига.При воздействии с силой F пружина удлиняется на величину $\Delta \ell=F/k_1$ , при этом коэффициент ее жесткости зависит от диаметра проволоки d, числа витков и диаметров витка D и оказывается равным

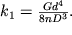
$k_1=\frac{G d^4}{8 n D^3}.$

(1.55a)

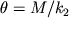
При закручивании пружины, подобно валу, вокруг ее оси, когда к торцевому ее сечению прикладывается момент внешних сил M, витки пружины испытывают деформации растяжения и сжатия (как при изгибе балки). В этом случае угол закручивания $\theta=M/k_2$ , где коэффициент пропорциональности

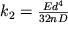
$k_2=\frac{E d^4}{32 n D}$

(1.55б)

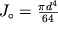
и зависит от момента инерции круглого сечения $J_{\circ}=\frac{\pi d^4}{64}$ (ф-ла (1.39)), числа витков n и диаметра витка D.

Назад | Вперед

Публикации с ключевыми словами: механика - гидродинамика - газодинамика - упругость Публикации со словами: механика - гидродинамика - газодинамика - упругость
См. также: Д'Аламбера-Эйлера парадокс Механика твердого тела. Лекции. Число Маха Вариационные принципы механики Конус Маха Бернулли уравнение Баротропное явление Все публикации на ту же тему >>

Мнения читателей [4]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце