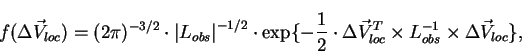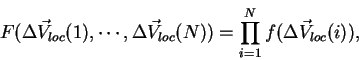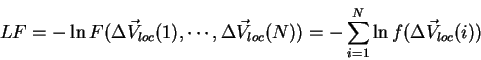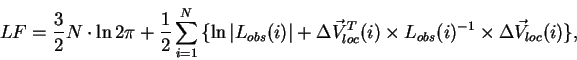Определение кривой вращения и шкалы расстояний в Галактике

---

<< 6. Наблюдаемый тензор ковариации | Оглавление | 8. Частный случай: чисто >>

Разделы

• Выбор значения R₀

---

7. Распределение остаточных скоростей и функция правдоподобия

Напомним, что под остаточной скоростью отдельной звезды мы понимаем разность между наблюдаемой и модельной скоростью. Трехмерная функция распределения остаточной скорости звезды , вычисляемой по формулам (10)-(12), может быть записана в общем виде [14]

где мы убрали явное упоминание о том, что используется принятая шкала расстояний, а и - соответственно определитель и обратная матрица наблюдаемого тензора ковариации (15). Функция распределения имеет смысл плотности вероятности определенного значения остаточной скорости конкретной звезды.

Поскольку объекты распределены в пространстве скоростей независимо друг от друга, их N-частичная (полная) функция распределения равна произведению функций (19) для всех звезд выборки (по теореме о произведении вероятностей независимых событий):

где - число объектов. Суть принципа максимального правдоподобия заключается в том, что мы считаем реальное распределение объектов нашей выборки наиболее вероятным из всех возможных. Следовательно, все параметры (описывающие модельное поле скоростей, а также - поправка шкалы расстояний), от которых зависит плотность вероятности распределения остаточных скоростей (19), должны быть подобраны так, чтобы вероятность на реальной выборке объектов достигала своего максимально возможного значения. Обычно решают задачу, минимизируя взятый с обратным знаком логарифм значения плотности вероятности, т.е. строят так наз. функцию правдоподобия

и сводят задачу к поиску минимума функции правдоподобия с использованием какого-либо эффективного алгоритма многомерной оптимизации. Подставив в (21) аналитическое выражение для функции (19), перепишем (21) в явном виде:

где индекс относится к текущему объекту выборки.

Практическое замечание: остаточная скорость и тензор ковариации для каждой звезды и, следовательно, значение функции правдоподобия , выражаются через известные из наблюдений величины и текущие значения подбираемых кинематических параметров выборки. Любая используемая для оптимизации программа ищет решение, обеспечивающее минимум функции (22), методом итераций, т.е. путем перебора возможных значений неизвестных параметров. Это замечание относится в равной степени к двумерному и одномерному случаям.

является функцией большого числа неизвестных параметров и, решив задачу оптимизации, мы обычно находим следующие параметры дифференциально вращающейся подсистемы:

- компоненты скорости локальной выборки звезд относительно Солнца;

- главные оси эллипсоида скоростей для выборки звезд (напомним, что они считаются одинаковыми для всей исследуемой области);

- угловая скорость вращения подсистемы на расстоянии Солнца и ее производные;

- искомая поправка к шкале расстояний;

Другие параметры поля скоростей, например, описывающие некруговые движения центроидов.

Если поставлена задача оценки кинематических параметров без уточнения шкалы расстояний, поправку шкалы во всех формулах следует положить равной 1, тогда принятые расстояния будут тождественны уточняемым.

Выбор значения R₀

Несколько слов следует сказать о выборе значения галактоцентрического расстояния Солнца . В современной литературе приводятся оценки этого важнейшего структурного параметра Галактики, заключающиеся в интервале от 7 до 8.5 кпк [18]. Дискуссия об этом все еще идет. Строго говоря, значение почти линейно связано с принятой шкалой расстояний. Попытки вычисления как одного из неизвестных параметров задачи (22) неоднократно предпринимались, но не приводили к надежным результатам. Более того, из-за корреляции с параметром шкалы расстояний одновременное уточнение шкалы и вычисление является совершенно некорректным. В принципе можно попытаться оценить методом последовательных приближений, меняя его значение после каждого нового шага по уточнению шкалы расстояний.

К счастью, вычисляемые кинематические параметры сравнительно слабо чувствительны к небольшим вариациям принимаемого значения . В 1985 г. МАС рекомендовал использовать значение кпк. Однако во многих работах последних лет выводится средневзвешенное значение кпк. Оно более соответствует короткой шкале расстояний. Рекомендуем использовать это значение как компромиссное. Отметим также, что прямые радиоинтерферометрические измерения тригонометрического параллакса радиоисточников в центре Галактики приводят к еще меньшим значениям .

---

<< 6. Наблюдаемый тензор ковариации | Оглавление | 8. Частный случай: чисто >>

Публикации с ключевыми словами: лучевая скорость - кривая вращения - Галактика - метод максимального правдоподобия Публикации со словами: лучевая скорость - кривая вращения - Галактика - метод максимального правдоподобия
См. также: Центр Галактики в инфракрасном свете Магнитное поле нашей Галактики от "Планка" Галактика-сад в Коне Огромные пузыри вокруг Млечного Пути в гамма-лучах Шаровое скопление M72 Холодная пыль вблизи нашей Галактики Панорама Млечного пути Все публикации на ту же тему >>