Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

Эффект аномального пропускания

 Эффект аномального пропускания

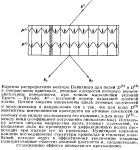
Резкое уменьшение поглощения части потока излучения в толстом идеальном кристалле при лауэвском пропускании. Эффект аномального пропускания впервые наблюдался X. Борманом в 1941 для рентгеновских лучей лучей (эффект Бормана), позднее исследован для нейтронов, электронов и гамма-лучей. Интерпретация эффекта предложена М. фон Лауэ (М. von Laue) в 1949.

Обычно интенсивность рентгеновских лучей при распространении в кристалле экспоненциально уменьшается с глубиной z проникновения излучения в кристалл:
$G(z)=G_0e^{\displaystyle -\mu_0(\omega)z}$,(1)

где G0 - интенсивность первичного поля; z - координата вдоль направления распространения; $\mu_0(\omega)={\displaystyle\omega\over\displaystyle c}|\gamma_i^0(\omega)|$ - линейный коэффициент фотоэлектрического поглощения среды; $\omega$ - частота излучения; $\gamma_i^0(\omega)$ - мнимая часть нулевой фурье-компоненты рентгеновской поляризуемости.

Зависимость (1) предполагает пространственную однородность поля излучения в кристалле или нерегулярное строение (искажение) кристалла и правильно описывает ослабление интенсивности излучения при его распространении в кристалле в произвольном (не дифракционном) направлении. Она также верна и при кинематической дифракции рентгеновских лучей в тонком (по сравнению с длиной первичной экстинкции) кристалле. Если толщина кристалла $d\gg\mu_0^{-1}$, то, согласно (1), излучение полностью поглощается в нем.

При динамической дифракции в условиях лауэвского пропускания значительная часть интенсивности поля проходит через толстые ($d\gg\mu_0^{-1}$) кристаллы, практически не ослабляясь. Это явление и называтеся эффектом аномального пропускания. При динамической дифракции в кристалле устанавливается пространственно-неоднородная структура поля с масштабом неоднородности порядка размеров элементарной ячейки кристалла. Для правильного описания ослабления интенсивности такого поля показатель экспоненты в (1) должен учитывать не только величину фотоэлектрического поглощения, но и пространственную структуру поля.

Наиболее благоприятным для наблюдения эффекта аномального пропускания случаем является симметричное лауэвское пропускание s-поляризованного излучения при точном выполнении условия Брэгга-Вульфа. При этом отражающие атомные плоскости перпендикулярны входной поверхности кристаллической пластины, а вектор дифракции $\vec g$ параллелен ей.

Рассмотрим эффект аномального пропускания для случая, когда имеется лишь 2 луча - один проходящий и один дифракционный (см. рис. 1 к ст. Дисперсионная поверхность). Согласно динамической теории дифракции, поле в кристалле в этом случае для каждой из двух (s и р) поляризаций (см. Поляризация света) состоит из четырех волн, попарно принадлежащих разным листам дисперсионной поверхности, описывающей зависимость волнового вектора от частоты излучения. Если кристаллографические плоскости центросимметричного кристалла при точном выполнении условия Вульфа-Брэгга перпендикулярны поверхности кристалла, то суммарная индукция электрического поля электромагнитной волны для каждого листа дисперсионной поверхности будет равна
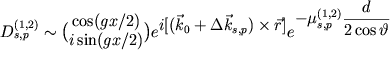$D_{s,p}^{(1,2)}\sim{\displaystyle\cos(gx/2)\choose\displaystyle i\sin(gx/2)}e^{\displaystyle i\lbrack(\vec k_0+\Delta\vec k_{s,p})\times\vec r\rbrack}e^{\displaystyle -\mu_{s,p}^{(1,2)}{\displaystyle d\over\displaystyle 2\cos{\vartheta}}}$,(1)

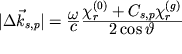где $\vartheta$ - угол Брэгга, $\vec g$ - вектор обратной кристаллической решетки, $\vec k_0$ - волновой вектор первичной волны, $|\Delta\vec k_{s,p}|={\displaystyle\omega\over\displaystyle c}{\displaystyle\chi_r^{(0)}+C_{s,p}\chi_r^{(g)}\over\displaystyle2\cos{\vartheta}}$ - добавка к z-компоненте вектора $\vec k_0$ за счет преломления, $\chi_{r,i}^{(0,g)}$ - действительная (r) и мнимая (i) части фурье-компонент рентгеновской поляризуемости, Cs=1, Ср = 2 cos $\vartheta$; линейные коэффициенты поглощения $\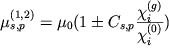mu_{s,p}^{(1,2)}=\mu_0(1\pm C_{s,p}{\displaystyle\chi_i^{(g)}\over\displaystyle\chi_i^{(0)}})$, где $\mu_0={\displaystyle1\over\displaystyle2}{\displaystyle\omega\over\displaystyle c}\chi_i^{(0)}$. Члены $\sim\chi_{r,i}^{(g)}$ в выражении для $\Delta\vec k_{s,p}$ и $\mu_{s,p}^{(1,2)}$ описывают влияние интерференции на преломление и поглощение излучения при дифракции. 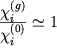Для s-поляризации из-за слабой зависимости $\chi_i^{(g)}$ от $\sin {\displaystyle\vartheta\over\displaystyle\lambda}$ отношение ${\displaystyle\chi_i^{(g)}\over\displaystyle\chi_i^{(0)}}\simeq1$ так что $\mu_s^{(1)}\simeq2\mu_0$, а $\mu_s^{(2)}\ll\mu_0$. Следовательно, излучение с $D_s^{(1)}$ поглощается сильнее, а с $D_s^{(2)}$ - слабее, чем в произвольном направлении. Поэтому через кристалл толщиной $d\gg\mu_0^{-1}$ может проходить только излучение с $D_s^{(2)}$. Прошедшее излучение имеет преимущественную s-поляризацию, так как для р-поляризации $\chi_i^{(g)}\cos2\vartheta/chi_i^{(0)}\lt1$ и эффект аномального пропускания выражен слабее. Эффект существует во всей угловой области дифракционного отражения, однако при увеличении отстройки $\Delta\vartheta$ от точного угла Брэгга $\vartheta$ он быстро ослабляется.

Векторы Пойнтинга полей $D_{s,p}^{(1,2)}$ в соответствии с (1) равны:
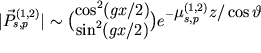$|\vec P_{s,p}^{(1,2)}|\sim{\displaystyle\cos^2(gx/2)\choose\displaystyle\sin^2(gx/2)}e^{-\displaystyle\mu_{s,p}^{(1,2)}z/ \cos\vartheta}$(2)

и направлены вдоль атомных плоскостей, а их амплитуды в направлении, перпендикулярном атомным плоскостям, модулированы с периодом, равным межплоскостному расстоянию. Вследствие этого $\vec P^{(1)}$ принимает максимальные значения на атомных плоскостях, а $\vec P^{(2)}$ - между ними (рис.). Т.к. основной вклад в фотоэлектрическое поглощение дают внутренние К- и L-оболочки, электронная плотность которых сосредоточена вблизи атомных ядер, поле $D^{(1)}$ распространяется в области повышенной электронной плотности, взаимодействует со средой и поглощается более интенсивно, а поле $D^{(2)}$ распространяется в области пониженной электронной плотности и взаимодействует со средой менее интенсивно, чем в произвольном, не дифракционном направлении. Этим и обусловлены аномально низкое поглощение в дифракционном направлении и появление резких максимумов на рентгенограмме.

Тепловые колебания атомов в кристалле эффективно увеличивают размеры атомов, так что $\mu_{s,p}^{(2)}$ возрастает. Например, при температуре $T\simeq$300 К
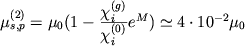$\mu_{s,p}^{(2)}=\mu_0(1-{\displaystyle\chi_i^{(g)}\over\displaystyle\chi_i^{(0)}}e^M)\simeq4\cdot10^{-2}\mu_0$,
где $e^M$ - фактор Дебая-Валлера. Эффект аномального пропускания зависит также от структуры кристалла. Любые отклонения от идеальных условий (атомные плоскости не перпендикулярны кристаллографическим плоскостям, наличие отстройки от точного угла $\vartheta$, дефектов) уменьшают эффект аномального пропускания. При многолучевой дифракции могут существовать области, где эффект аномального пропускания проявляется еще сильнее.

Эффект аномального пропускания используется для исследования совершенства строения кристаллов (см. Рентгеновская топография) и получения слаборасходящихся пучков монохроматического поляризованного рентгеновского излучения. Эффект аномального пропускания имеет место и для других излучений.


Глоссарий Astronet.ru

L | R | А | Б | В | Г | Д | Е | Ж | З | И | Й | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Щ | Э | Ю | Я 
Публикации с ключевыми словами: кристаллы - поглощение света - аномальное пропускание
Публикации со словами: кристаллы - поглощение света - аномальное пропускание 		Карта смысловых связей для термина ЭФФЕКТ АНОМАЛЬНОГО ПРОПУСКАНИЯ
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 2.9 [голосов: 80]
 
О рейтинге
Версия для печати Распечатать
Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования