| предыдущая |
Адиабатическая сжимаемость и другие производные
Помимо давления как функции температуры и плотности, от термодинамики требуется также знание некоторого количества производных, характеризующих изменение свойств вещества в процессах, происходящих при тех или иных условиях.
Классическим примером таких производных являются производные давления по температуре и плотности при фиксированных плотности и температуре, соответственно. Хотя знание давления предполагает возможность (хотя бы в принципе) вычисления таких производных, при рачетах структуры звезд чаще используют именно эти производные вместо самого уравнения состояния - дело в том, что давление входит в уравнения как производная, и чтобы использовать уравнение состояния вместе с дифференциальными уравнениями равновесия, мы должны либо выразить плотность как функцию давления и температуры, либо записать уравнение состояния в дифференциальной форме (для постоянного химического состава)
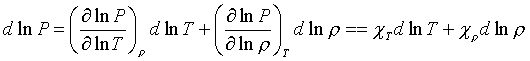
где в правой части введены упомянутые производные.
Более сложными для вычисления являются производные, связанные с теплоемкостями. В общей форме под теплоемкостью понимают величину
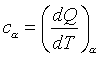
индекс ![]() указывает
на условия, при которых происходит измерение теплоемкости. Наиболее важной является
теплоемкость при постоянном объеме, поскольку в этом случае мы измеряем изменение
внутренней энергии
указывает
на условия, при которых происходит измерение теплоемкости. Наиболее важной является
теплоемкость при постоянном объеме, поскольку в этом случае мы измеряем изменение
внутренней энергии
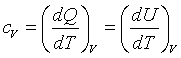
В действительности, cV это величина, которая не может быть вычислена по одному уравнению состояния, и это величина, которая достаточна для вычисления всех других величин в классической термодинамике. Например, теплоемкость при постоянном давлении cP выражается следующей формулой
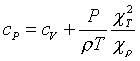
Адиабатические производные
В многих вопросах строения и устойчивости звездных конфигураций принципиальную роль играют безразмерные адиабатические показатели, определяемые следующими соотношениями
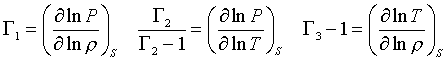
Индексы S указывают на то, что производные предполагаются адиабатическими (при постоянной энтропии), то есть в процессе изменений параметров не происходит теплообмена с окружающей средой. В этих произвдных легко узнать адиабатическую сжимаемость газа (относительное изменение объема при сжатии), адиабатический градиент температуры, и температурный коэффициент расширения. Между ними существует тождественное соотношение
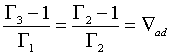
В обобщенном смысле, ![]() 1 определяет динамическую
устойчивость вещества, а
1 определяет динамическую
устойчивость вещества, а ![]() 2 и
2 и ![]() 3
- конвективную и тепловую (пульсационную) соответственно.
3
- конвективную и тепловую (пульсационную) соответственно.
Для вычисления адиабатических показателей используются формулы
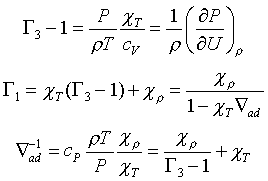
Таблица содержит предельные значения некоторых из перечисленных производных для компонент, составляющих плазму звезд
| идеальный газ |
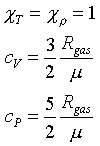 |
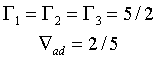 |
| чернотельное излучение |
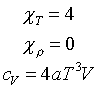 |
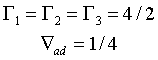 |
| сильновырожденный электронный газ |
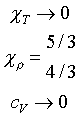 |
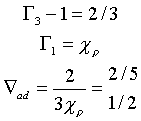 |
| частично ионизованный газ |
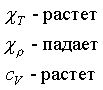 |
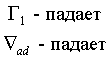 |
В.Батурин
| предыдущая |
|
Публикации с ключевыми словами:
Сверхновые - звезды - сверхгигант - нейтронные звезды - красный гигант - бурый карлик - диаграмма Герцшпрунга-Рессела - белый карлик - Эволюция звезд - термоядерные реакции - вырожденный газ - гидростатическое равновесие - конвекция - лучистый перенос - главная последовательность - эволюционный трек звезды - карлики
Публикации со словами: Сверхновые - звезды - сверхгигант - нейтронные звезды - красный гигант - бурый карлик - диаграмма Герцшпрунга-Рессела - белый карлик - Эволюция звезд - термоядерные реакции - вырожденный газ - гидростатическое равновесие - конвекция - лучистый перенос - главная последовательность - эволюционный трек звезды - карлики | |
См. также:
Все публикации на ту же тему >> | |