---

<< 14. ГВ астрономия | Оглавление | 14.2 Детектирование ГВ >>

14.1 Описание

Согласно теории гравитации А.Эйнштейна (общей теории относительности, ОТО), любая плотность энергии может быть описана в терминах гравитационного поля, а само гравитационное поле наглядно представляется как искривление пространства-времени, в котором находится материя^14.2. Искривление означает, что квадрат интервала между двумя событиями в присутствии материи отличается от квадрата интервала в специальной теории относительности , а именно, перед квадратом элемента времени и длины появляются коэффициенты, зависящие от координат и времени. 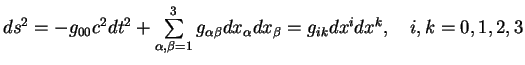В общем случае можно записать (по повторяющимся индексам подразумевается суммирование, время считается координатой с нулевым индексом). Квадратная симметричная матрица называется метрикой пространства-времени. Т.о. в общем случае имеется 10 независимых величин , которыми характеризуется гравитационное поле. Напомним, что в Ньютоновской гравитации достаточно одного скалярного гравитационного потенциала , вычисляемого из пространственного распределения плотности с помощью уравнения Пуассона .

Физический смысл коэффициентов метрики ясен из их вида в приближении слабого поля^14.3: для сферически-симметричного невращающегося тела , . Сила, действующая на пробные тела (напряженность гравитационного поля) определяется градиентом потенциала в Ньютоновской теории и в общем случае - производными метрики по координатам и времени.

В обычных земных условиях метрика очень мало отличается от метрики пустого пространства (т.н. метрики Минковского) ^14.4. Для слабого гравитационного поля можно линеаризовать метрику, записав , где - малое возмущение координат и времени. Линеаризация уравнений ОТО без источника поля в правой части приводит к волновому уравнению ( - оператор Д'Аламбера), которое описывает распространение волны со скоростью света в пустом пространстве.

До середины 60-х годов шли теоретические споры, представляют ли гравитационные волны физическую реальность или они являются математической фикцией. Однако в настоящее время доказано, что гравитационные волны переносят энергию и импульс, которые могут передавать макроскопическим телам. Образно можно представить себе гравитационную волну как мелкую "рябь" на поверхности океана, причем большой радиус кривизны океана представляет собой фоновую кривизну пространства-времени, на которой распространяются волны, а взаимодействие с макроскопическими телами - как качание "лодки" на этой ряби. ^14.5

Обычно рассматривают плоские волны (что вполне оправдано для удаленных источников) и для описания их взаимодействия с макроскопическими телами выбирают специальную систему координат, в которой описание взаимодействия ГВ с макроскопическими телами приобретает наиболее простой вид (ясно, что выбор системы координат не должен сказываться на физических эффектах). Фиксация системы координат в четырехмерном пространстве-времени накладывает 8 дополнительных условий, и тогда из 10 независимых величин реально независимыми оказываются только две, которые называют и поляризацими (приняты обозначения ) в соответствии с тем, как действуют эти волны на пробные тела (см. 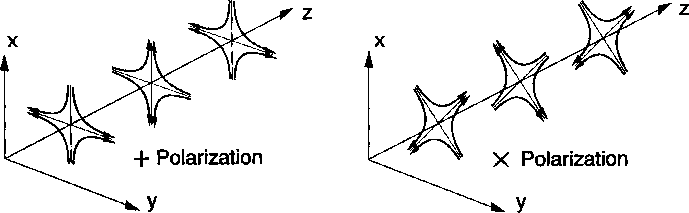Рис. 14.1).

Подобно тому, как заряженная частица в поле плоской электромагнитной волны начинает совершать колебания, взаимодействие гравитационной волны с макроскопическими телами приводит к появлению относительных ускорений и к изменению физического расстояния между ними. Например, относительное изменение расстояния между двумя пробными телами в поле плоской ГВ

где - линейная комбинация плюс- и кросс- поляризаций ГВ, зависящая от ориентации тел относительно направления распространения волны. Это соотношение наглядно показывает, что по своему физическому смыслу амплитуда ГВ является безразмерной величиной. Часто ее называют "безразмерной амплитудой возмущений метрики", создаваемых проходящей ГВ.

---

<< 14. ГВ астрономия | Оглавление | 14.2 Детектирование ГВ >>

Публикации с ключевыми словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика Публикации со словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика
См. также: Местное межзвездное облако Черная дыра разрушает звезду: анимация Звезды, пыль и туманность в NGC 6559 25 самых ярких звезд на ночном небе Анимация: черная дыра разрушает звезду Разложение далекого света Сравнение размеров звезд Все публикации на ту же тему >>