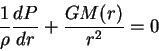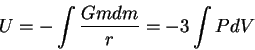<< 5.3 Протозвезды. | Оглавление | 6. Звезды (продолжение) >>
- 5.4.1 Гидростатическое равновесие
- 5.4.2 Теорема вириала
- 5.4.3 Тепловая устойчивость звезд. Отрицательная теплоемкость
5.4 Стационарные звезды
Физическое состояние стационарных звезд определяется
условиями гидростатического равновесия (когда
макроскопические параметры -
масса, радиус - изменяются на больших временах 
динамического времени
) и теплового
равновесия (несмотря на мощное энерговыделение в центре,
звезды не взрываются, их светимость меняется плавно).
5.4.1 Гидростатическое равновесие
Рассмотрим объем вещества 
с давлением 
. Сила, стремящаяся
расширить объем
, где 
-
элемент поверхности. Очевидно, если нет градиента давления
(
) 
. В общем случае имеем:
откуда
. Т.о. сила, действующая на элемент объема
Сила гравитационного притяжения, действующая на объем - массовая,
действует на элемент 
,
, где
- ньютоновский гравитационный
потенциал. Суммарная сила, действующая на элементарный объем в звезде
т.о.
Для сферически-симметричного случая
,
и
Для оценок по порядку величины
можно пользоваться приближенной формой уравнения
гидростатического равновесия
и 
- масса и радиус звезды.
Эта формуля дает хорошее приближение для центрального давления
в самогравитирующем газовом шаре.
5.4.2 Теорема вириала
Прямым следствием уравнения гидростатического равновесия (5.5)
является теорема вириала, связывающая тепловую (кинетическую)
и потенциальную (гравитационную) энергию стационарной звезды.
Умножая обе части уравнения гидростатического равновесия на 
и интегрируя по 
по частям, приходим к
, удельная энергия на 1 г вещества есть
, получаем
где
- тепловая энергия.
Пример 1. Оценим температуру в центре Солнца. Пусть вся звезда
состоит из идеального одноатомного газа, 
.
, 
и
находим
(с учетом молекулярного веса полностью
ионизованной плазмы состоящей по массе на 75 
из
водорода и на 25 из гелия
)
K. Точное
значение - 14 млн. градусов.
Пример 2. Физически важные случаи:
1) . Этот показатель адиабаты
соответствует идеальному одноатомному газу, а также нерелятивистскому
вырожденному ферми-газу. Получаем
т.е. знакомый вид теоремы вириала в механике для движения
тел в потенциале 
.
2) 
. Этот показатель адиабаты характерен для газа
из релятивистских частиц (например, фотонов), когда связь между давлением и
плотностью энергии 
, или для релятивистского вырожденного
ферми-газа. В этом случае теорема вириала для самогравитирующей конфигурации
дает 
, 
, т.е. такая
конфигурация находится в положении безразличного равновесия:
Очевидно, полная энергия
является линейной функцией
и равновесие (
) возможно
только при
. При 
полная энергия положительна,
, т.е. система не связанная, и при
малых возмущениях распадается,
.
При 
полная энергия
отрицательна, 
при малых возмущениях
система коллапсирует (
).
Потеря устойчивости всегда происходит в
динамической шкале времени,
.
5.4.3 Тепловая устойчивость звезд. Отрицательная теплоемкость.
Рассмотрим теорему вириала для одноатомного идеального газа,
хорошее приближение для вещества нормальных звезд ():
,
, т.е.
сообщение энергии звезде (
) приводит к ее
охлаждению, 
, а излучение энергии (
) -
к разогреву , 
. Иными словами,
звезда, находящаяся в гидростатическом равновесии
(т.е. подчиняющаяся теореме вириала) обладает отрицательной теплоемкостью:
(здесь 
- теплоемкость газа звезды),
.
Замечание: теорема об отрицательной теплоемкости
справедлива для любой стационарной системы в поле тяготения -
например, спутник на стационарной орбите вокруг Земли:
при торможении спутника в атмосфере (отбор энергии от системы
Земля-спутник) он переходит на более низкую орбиту
с увеличением скорости (
).
Пусть 
- подвод тепла к звезде (термоядерные реакции),
- отвод энергии (например, излучением с поверхности).
В равновесии имеем
. Изменение температуры
со временем находим из уравнения теплового баланса
Разлагая правую часть в ряд вблизи точки
имеем
В нормальных звездах
,
и
коэффициент в правой части положителен, откуда
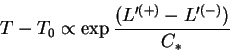
В системах с положительной теплоемкостью разница температур экспоненциально возрастает (ср. взрыв тротила), в звездах же с отрицательной теплоемкостью рост флюктуаций температуры невозможен - звезды находятся в устойчивом тепловом равновесии.
Характерное время установления теплового равновесия в звезде
(т.н. тепловое время, или время Кельвина-Гельмгольца) грубо можно
определить из теоремы вириала, приняв за оценку время, необходимое для
потери запаса тепловой энергии при заданном темпе отвода энергии
(т.е. светимости 
). Имеем
,
, 
).
В XIX в. Кельвин и Гельмгольц таким образом оценивали время жизни Солнца.
Любопытно, что Кельвин не принимал теорию эволюции Дарвина
(которая требовала миллиардов лет для развития видов) на
основании своего заключения о возрасте Солнца в 30 млн. лет!
В
начале ХХ в. стало ясно, что возраст Земли намного превосходит 30
млн. лет - возникла необходимость поиска источника энергии на Солнце.
Таким источником являются термоядерные реакции синтеза тяжелых
элементов из водорода и гелия.
ЛИТЕРАТУРА
1. С.А.Каплан. Физика звезд. 3 изд. М.: Наука, 1977
2. Я.Б.Зельдович, С.И.Блинников, Н.И.Шакура. Физические основы строения и эволюции звезд. М.: МГУ, 1982
<< 5.3 Протозвезды. | Оглавление | 6. Звезды (продолжение) >>
|
Публикации с ключевыми словами:
звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика
Публикации со словами: звезды - Межзвездная среда - Космология - теоретическая астрофизика - астрофизика | |
См. также:
Все публикации на ту же тему >> | |
