Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Физические основы строения и эволюции звезд
<< 9.5 Устойчивость релятивистских звезд | Оглавление |

9.6 Несферические поля тяготения

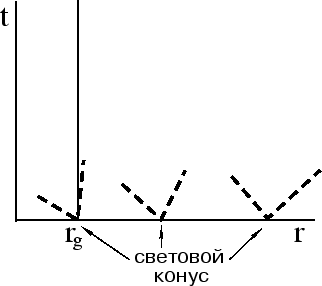
Наиболее характерное свойство поля Шварцшильда -- то, что на некотором расстоянии ($ r<r_g$) невозможен покой частиц. Сфера Шварцшильда касательна световому конусу (см. рис. 61), поэтому никакие частицы (в том числе и ультрарелятивистские) не могут выйти из-под радиуса $ r_g$, т. е. сферу Шварцшильда можно пересечь только снаружи внутрь. Решение Шварцшильда относится к случаю сферически-симметричного распределения вещества. Мы знаем, что идеальных сферически-симметричных объектов не существует. Поэтому возникает естественный вопрос -- насколько свойства этого решения устойчивы относительно возмущений сферической симметрии?

Устойчивость шварцшильдовской сингулярности относительно малых возмущений метрики исследовали Редже и Уилер. Они пришли к выводу, что для стационарных возмущений есть поля только двух типов -- с особенностью или на поверхности Шварцшильда или на бесконечности. Сразу возникает подозрение, что поверхность Шварцшильда может быть неустойчива.

Рис. 61.

Методом Редже-Уилера можно исследовать устойчивость только относительно малых возмущений. Другой путь (позволяющий исследовать большие возмущения) -- это получение точных решений уравнений ОТО, в которых снято требование сферической симметрии. Статические решения для осесимметричного распределения масс очень давно получил Вейль. В этом решении источник поля (т. е. некоторое тело) предполагается ограниченным. Поэтому на бесконечности метрика должна переходить в евклидову. Решение Вейля в частном случае совпадает с решением Шварцшильда (строго говоря, его можно перевести в решение Шварцшильда некоторым преобразованием координат).

А в общем случае существует квадрупольный момент гравитационного поля. В этом решении поверхность $ g_{00}=0$ обладает совсем другими свойствами, чем сфера Шварцшильда (где $ g_{00}=1-r_g/r=0$ при $ r=r_g$). В частности, на поверхности $ g_{00}=0$ есть истинная особенность пространства-времени. В метрике Шварцшильда инвариант

$\displaystyle C=R_{iklm}R^{iklm}=12/r_g^2$   при$\displaystyle \,r=r_g, $

т. е. истинной особенности нет (хотя $ g_{11}=(1-r_g/r)^{-1}\longrightarrow\infty$, однако в действительности пространство гладко -- есть системы отсчета, где все $ g_{ik}$ -- гладкие до центра; это значит просто, что метрика Шварцшильда в обычной записи не годится для описания пространства при $ r<r_g$). В решении Вейля $ C$ имеет особенность на поверхности $ g_{00}=0$:

$\displaystyle C=A\,q^2\,g_{00}^{-1}+12/r_g^4+...\;, $

где $ q$ -- квадрупольный момент. Кроме того, в отличие от поля Шварцщильда, свет достигает этой поверхности за конечное время. Это отражает свойства, найденные Редже и Уилером: те возмущения, которые конечны на бесконечности, имеют особенность на поверхности $ g_{00}=0$.

Эти выводы не являются свойством специально квадрупольного отклонения от сферической симметрии. Можно показать, что они являются общими для любого статического аксиально-симметричного решения.

Могут ли реальные тела создать поле Вейля во всей области $ g_{00}>0$? Как уже говорилось, на бесконечности, в евклидовой области, поле Вейля соответствует гравитационному полю статического тела с неравным нулю квадрупольным моментом. Однако статическое тело не может дать такое поле вплоть до поверхности $ g_{00}=0$ уже потому, что тогда обращается в бесконечность гравитационная сила. Это было верно и в поле Шварцшильда, но мы знаем, что его можно реализовать нестатическими телами, движущимися сферически-симметричным образом (коллапсар).

Нельзя ли реализовать решение Вейля нестатическими телами? Оказывается и это невозможно. Можно показать, что при коллапсе в сопутствующей системе отсчета момент перехода границе тела поверхности $ g_{00}=0$ ничем не выделен: в этот момент на поверхности тела нет истинных особенностей пространства-времени ( $ C\ne\infty$), а в решении Вейля они есть. Итак, появление истинной особенности в этом решении означает, что такое распределение масс реализовано быть не может. Это связано с тем, что уравнения поля одновременно являются уравнениями движения.

Совершенно так же можно убедится, что рассмотрение статически малых возмущений решения Шварцшильда, проведенное Редже и Уилером, говорит не о неустойчивости этого решения, а о физической невозможности реализовать такие возмущения. Точнее говоря, статические возмущения поля Шварцшильда можно получить, только поместив сферу Шварцшильда во внешнее возмущающее поле. В решении Редже-Уилера это соответствует возмущениям конечным на $ r_g$ и расходящимся на бесконечности.

Имеются осесимметричные решения уравнений ОТО в вакууме ($ R_{ik}=0$) и другого типа -- это решение Керра. Приведем метрику Керра в виде, данном Боейром и Линдквистом:

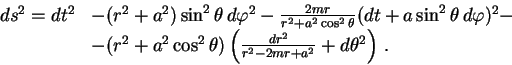\begin{displaymath}\begin{array}{ll} ds^2=dt^2&-(r^2+a^2)\sin^2\theta\,d\varphi^... ...eft({dr^2\over{r^2-2mr+a^2}}+d\theta^2\right)\,.\cr \end{array}\end{displaymath} (9.8)

Мы записали выражение для $ ds^2$ в таких единицах, что $ c=1,\,G=1$. Смысл символов $ m$ и $ a$, как всегда, находим исследованием предельных случаев. Сразу видно, что при $ a\longrightarrow0$ метрика Керра переходит в решение Шварцшильда, т. е. $ m$ можно интерпретировать как массу тела (в наших единицах $ r_g=2m$). Смысл символа $ a$ выясняется при переходе к бесконечности $ r\longrightarrow\infty$. Очевидно, тогда

$\displaystyle g_{00}=-g_{11}^{-1}=1-r_g/r, $

так же как для поля Шварцшильда. Но есть и одно существенное отличие:

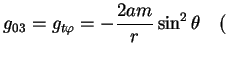$\displaystyle g_{03}=g_{t\varphi}=-{2am\over r}\sin^2\theta\quad($при$\displaystyle r\longrightarrow\infty), $

т. е. недиагональная компонента метрики $ g_{03}$ отлична от нуля. В ОТО показывают (см., например, ``Теорию поля'' Ландау и Лифшица), что в слабом поле (т. е. при $ r\longrightarrow\infty$) у вращающегося тела с моментом вращения $ K$ появляется компонента $ g_{03}$ именно такого вида:

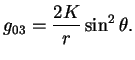
$\displaystyle g_{03}={2K\over r}\sin^2\theta. $

Это позволяет считать, что метрика Керра описывает внешнее поле тела, вращающегося с моментом

$\displaystyle K=-am. $

При получении выражения для $ g_{03}$ в случае $ r\longrightarrow\infty$ мы по существу вели разложение по степеням $ a/r$, поэтому это выражение остается справедливым и в сильном поле вплоть до $ r\longrightarrow r_g$, если $ a\longrightarrow0$. Метрика, записанная в виде (), имеет смысл только при $ 0\le a\le m$, т. е. $ a=m$ соответствует максимально возможному моменту центрального тела (т. е. $ K_{\rm {max}}=m^2$ или в обычных единицах $ K_{\rm {max}}=Mcr_g/2=GM^2/c$).

Если подсчитать скаляр кривизны $ C$, то окажется, что метрика имеет особенность только при $ r=0$. это наталкивает на мысль, что метрика Керра в отличие от метрики Вейля может быть реализована реальными телами.

Рассмотрим, во что переходит поверхность Шварцшильда в метрике Керра. В шварцшильдовском случае сфера $ r=r_g$ обладала двумя главными свойствами: на ней $ g_{00}=0$ и, кроме того, ее касался световой конус. Из-за второго свойства сфера Шварцшильда являлась как бы ``клапаном'': никакие частицы не могли пересечь ее изнутри наружу. Этот клапан, т. е. поверхность, касательную световому конусу, называют ``горизонтом событий''. В метрике Керра оказывается, что поверхность $ g_{00}=0$ и горизонт событий не совпадают. Можно найти, что поверхность $ g_{00}=0$ определяется выражением

$\displaystyle r_{\mbox{ш}}=m+\sqrt{m^2-a^2\cos^2\theta}\,, $

а горизонт событий

$\displaystyle r_{\mbox{гор}}=m+\sqrt{m^2-a^2}\,. $

Очевидно, что $ r_{\mbox{ш}}\ge r_{\mbox{гор}}$. Так же как в поле Шварцшильда условие $ g_{00}\ge 0$ ограничивает область, где можно покоится. Однако в метрике Шварцшильда $ r_{\mbox{ш}}=r_{\mbox{гор}}$. Поэтому частицы с $ r<r_{\mbox{ш}}$ могли двигаться только к центру. Теперь частицы с $ r<r_{\mbox{ш}}$, но $ r>r_{\mbox{гор}}$ могут двигаться по радиусу в любую сторону, в частности, может быть $ r=$const (хотя для них невозможно $ \varphi =$const, они обязаны двигаться по $ \varphi$ в ту же сторону, что вращается тело). Область $ r_{\mbox{гор}}\le r \le r_{\mbox{ш}}$ называют эргосферой.

Как будет меняться метрика в присутствии свободно падающих частиц? Частицы, которые движутся навстречу вращению тела, захватываются раньше. Поэтому, если на центральное тело падают частицы, имеющие изотропное распределение по скоростям на бесконечности, то метрика Керра теряет момент и переходит в метрику Шварцшильда, а облако частиц приобретает момент (так как частицы захватываются выборочно).

Приведем выражение для прицельного параметра гравитационного захвата частицы, движущейся в экваториальной плоскости:

        а) при $ v_{\infty}\ll c$:

$\displaystyle l={c\over{v_{\infty}}}\left[1+\left(1\pm{\vert a\vert\over m}\right)^{1/2}\right]r_{\mbox{ш}} $

(выбор знака зависит от направления момента частицы относительно момента центрального тела). При $ a=0,\,l=(2c/v_{\infty})r_g$:         б) при $ v_{\infty}=c$ (здесь тоже важен знак момента частицы):

$\displaystyle l_+=4\cos^3\left[{1\over 3}(\pi-\arccos\vert a/m\vert)\right]r_{\mbox{ш}}, $

$\displaystyle l_-=4\cos^3\left[{1\over 3}\arccos\vert a/m\vert\right]r_{\mbox{ш}}. $

Рис. 62.

Зависимость параметров захвата в метрике Керра от знака момента интересно проявляется в случае дисковой аккреции. Торн показал, что при $ a\ll m$ свет, излучаемый веществом при аккреции, поглощается черной дырой так, что $ a\longrightarrow m$. Однако, если $ a$ почти равно $ m$, то момент отбирается. Устойчивое значение $ a=0,948\,m$.

Пенроуз показал, что есть возможность извлекать энергию из поля Керра. Бросим частицу так, чтобы она в эргосфере ( $ r_{\mbox{гор}}\le r \le r_{\mbox{ш}}$) распадалась на две частицы. Пусть одна из новых частиц уйдет под горизонт, а вторая вылетит из-под $ r_{\mbox{ш}}$ (рис. 62). Можно осуществить этот процесс так, что вернувшаяся частица принесет энергии больше, чем отправленная. Ясно, что при этом уменьшается энергия центрального тела.

Возникает задача: сколько энергии можно отнять у черной дыры? Хокинг показал, что есть некоторая инвариантная масса, которую процессами такого рода нельзя уменьшить. В метрике Шварцшильда площадь сферы $ r=r_g$ равна

$\displaystyle S=4\pi r_g^2=16\pi m^2. $

В метрике Керра можно подсчитать площадь горизонта событий:

\begin{displaymath} \begin{array}{ll} S=\int &\sqrt{g_{22}g_{33}}\,d\theta\,d\va... ...a^2)^{1/2})^2+a^2]=8\pi m[m+(m^2-a^2)^{1/2}]\,. \cr \end{array}\end{displaymath}

Теорема Хокинга состоит в том, что $ S$ не может уменьшаться. Это позволяет определить инвариантную массу черной дыры

$\displaystyle S\equiv 16\pi m^2_{\rm inv}\,. $

Подобные исследования показали, что при очень общих предположениях единственным точным осесимметричным решением с отсутствием сингулярности на горизонте событий является решение Керра. Можно показать, что при коллапсе под $ r_{\mbox{гор}}$ любого вращающегося тела метрика Керра возникает как предельная при $ t\longrightarrow\infty$ для всей области вне $ r_{\mbox{гор}}$. Все это позволяет считать, что метрика Керра описывает поле любой вращающейся черной дыры. Отметим, что реальная черная дыра должна иметь момент вращения $ a$ скорее ближе к $ a=m$, чем к $ a=0$. В размерных единицах $ a=m$ соответствует моменту $ K=GM^2/c$. Для $ M=1\,M_\odot$ это дает значение порядка момента вращения Солнца. Но Солнце -- это очень медленно вращающаяся звезда. У массивных звезд удельный момент вращения может быть на два порядка больше.


<< 9.5 Устойчивость релятивистских звезд | Оглавление |

Публикации с ключевыми словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.0 [голосов: 120]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования