<< 4.5 Устойчивость теплового потока | Оглавление | 5. Ядерные реакции >>
4.6 Конвекция
Уравнения равновесия позволяют исследовать устойчивость звезды относительно сжатия
или расширения без перестановки слоев. Из вариационного принципа мы знаем, что
при
энергия имеет минимум, звезда устойчива относительно таких возмущений.
Следующий вопрос -- устойчива ли она относительно перестановки слоев. Сферически-
симметричными движениями в пределах гидродинамики невозможно переставить слои
вещества: появляются бесконечные 
. Поэтому необходимы более сложные
движения.
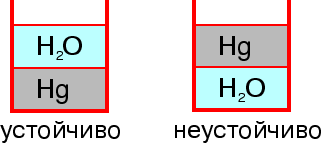
Рассмотрим, например, равновесие двух несжимаемых жидкостей с различной плотностью (вода и ртуть), рис. 24. Ситуация, в которой более тяжелая жидкость находится сверху, может быть устойчивой относительно плоских движений, но, рассматривая более широкий класс возмущений, например опрокидывание, получим выигрыш энергии. Таким образом, картина устойчива только тогда, когда снизу находится более тяжелая жидкость.
З а д а ч а 1. Проверьте это методом малых возмущений.
З а д а ч а 2. Проверьте, что и в случае сферически-симметричного распределения
несколько несжимаемых жидкостей разной плотности гравитационная энергия
минимальна, когда внутри более плотная несжимаемая жидкость.
В звездах плотность падает с высотой. Это еще не значит, что они обязательно устойчивы относительно перестановок слоев. Для ответа на вопрос об устойчивости мы должны привести два разных элемента к одинаковому давлению и сравнить их плотности. Если при этом плотность поднятого элемента окажется меньше, то такое распределение плотности неустойчиво. Рассмотрим, например, одноатомный газ:
-- энтропия, 
-- универсальная газовая постоянная. Если два
элемента привести к одинаковому давлению, то, очевидно, мерой плотности, а значит
и величиной, от которой зависит критерий устойчивости, будет энтропия этих
элементов. При адиабатических смещениях энтропия сохраняется и распределение будет
устойчивым, когда растет с высотой, так как при этом поднявшийся элемент окажется
тяжелее окружающего газа. Таким образом, при 
конфигурация устойчива,
при 
-- неустойчива. В частности, изотермическая атмосфера всегда устойчива,
но адиабатическое распределение (
) находится на грани устойчивости.
Обычно 
, т.е. для устойчивости необходимо
. В противном
случае замена слоев энергетически выгодна. Наименьшее значение адиабатический
градиент достигает в области ионизации -- вся энергия идет на ионизацию. Обычно
эти области конвективно неустойчивы.
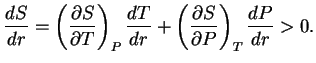
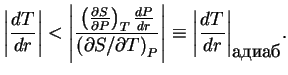
В области, где лучистое равновесие дает , возникает неустойчивость, поэтому
задачу приходится решать в два приема. Сначала предположим, что конвекции нет,
решим задачу о лучистом переносе и найдем равновесное распределение. В результате
получим распределение энтропии 
. В областях, где растет с радиусом,
решение устойчиво, но там, где падает, нужно сконструировать новое решение
с конвективным переносом энергии
(см. рис. 25).
В области конвекции практически
const.
Внешняя конвективная зона наблюдается на ближайшей к нам звезде -- Солнце. Наличие
этой зоны приводит к ряду замечательных явлений. Появляющийся в результате конвекции
механический поток энергии нагревает корону до температуры порядка 
K и
приводит к истечению солнечного ветра. Взаимодействие конвекции и вращения приводит
к генерации магнитного поля, образованию пятен и активности Солнца. Эти интересные
явления составляют предмет отдельной науки -- физики солнечной активности, которая
выходит за рамки нашего курса. Нужно только помнить, что Солнце -- самая обычная
и очень спокойная звезда. На других звездах могут происходить подобные явления
или еще более мощные. По-видимому, некоторые из них мы наблюдаем в виде вспышек
карликовых звезд (аналогичных хромосферным вспышкам на Солнце), но большинство
из них пока недоступны нашим приборам. Развитие наблюдений, например, рентгеновской
астрономии скоро сделает эти проблемы насущными для физики звезд.
<< 4.5 Устойчивость теплового потока | Оглавление | 5. Ядерные реакции >>
|
Публикации с ключевыми словами:
Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы
Публикации со словами: Эволюция звезд - внутреннее строение звезд - термоядерные реакции - физические процессы | |
См. также:
Все публикации на ту же тему >> | |
