Rambler's Top100Astronet    
  по текстам   по ключевым словам   в глоссарии   по сайтам   перевод   по каталогу 		 

На первую страницу
Поверхностная фотометрия галактик
<< 3. Представление результатов поверхностной | Оглавление | 3.2 Фотометрические параметры >>


3.1 Графические способы

рис.  4: Слева: репродукция изображений галактик NGC 3379 (справа), NGC 3384 (слева вверху) и NGC 3389 (слева внизу) (размер репродукции - 16.$'$6$\times$12.$'$4). Справа -- карта изофот галактик.
\begin{figure}\centerline{\psfig{file=fig4.ps,angle=-90,width=16.5cm}}\end{figure}

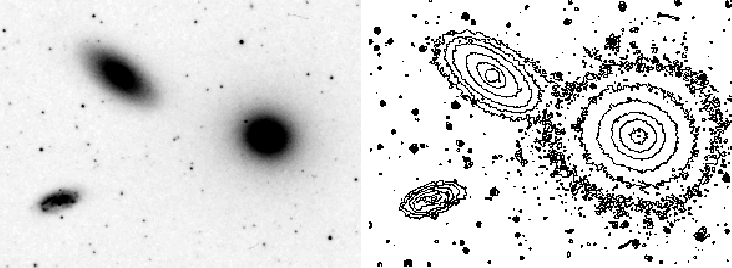
Простейшим способом представления результатов является их визуализация путем построения изображений в условных цветах и карт изоуровней (изофот). Как видно на рис. 4, где показаны изображения трех галактик, построенных с помощью Цифрового Обзора Неба (DSS2), карты изофот позволяют получить больше информации об объектах, чем простое репродуцирование их изображений. На картах можно одновременно оценить структуру как центральных частей галактик, так и предельно слабых внешних областей. Кроме того, изофоты позволяют грубо оценить закон распределения поверхностной яркости. Карты изофот строятся до какого-либо фиксированного слабого уровня поверхностной яркости (например, до $\mu(B)=26.0$). Шаг изофот обычно берется постоянным (например, $\Delta\mu=0.5$ или 1.0), хотя это может зависеть от конкретной задачи.

Для количественного анализа структуры галактик двумерные данные часто редуцируют в одномерные профили поверхностной яркости -- $\mu(r)$. Способов построения одномерных профилей из двумерных матриц существует довольно много и их широкое применение часто приводит к путанице в терминологии. Очевидно, что нет одного профиля, наилучшим образом характеризующего распределение яркости во всех галактиках. Нужно выбирать профили яркости в соответствии с конкретными целями исследования и с морфологическими особенностями объектов. (В дальнейшем слова ``профиль яркости'' или ``фотометрический профиль'' будут использоваться как общее наименование построенных разными способами одномерных распределений, характеризующих распределение яркости в галактиках.) Далее мы рассматриваем наиболее распространенные фотометрические профили.

$\bullet$ Фотометрический разрез

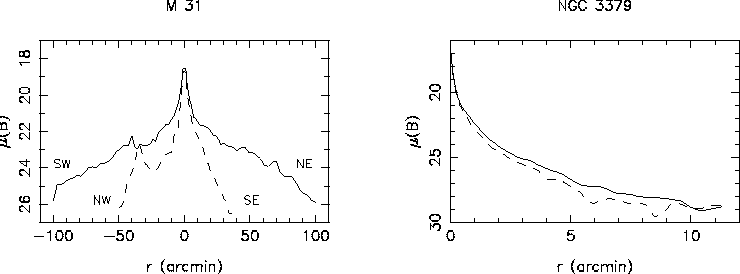
Фотометрический разрез -- это сечение галактики вдоль какого-либо фиксированного направления. Как правило, разрезы строят вдоль большой и малой оптических осей галактики, а также через наиболее интересные образования в их структуре (например, через области HII, вдоль и поперек бара, через приливные образования и т.д.). При представлении разрезов их иногда усредняют относительно центра галактики. Вдоль выбранных разрезов обычно изображается не только распределение поверхностной яркости в одной или нескольких цветовых полосах, но и распределение показателей цвета. Примеры фотометрических разрезов для ближайшей яркой спиральной галактики M 31 и для эллиптической галактики NGC 3379 (она является стандартом для галактической фотометрии) показаны на рис. 5.

рис.  5: Фотометрические разрезы галактик M 31 [5] и NGC 3379 [38]. Для NGC 3379 показаны разрезы, усредненные относительно ядра. Непрерывные линии -- разрезы вдоль больших осей, штриховые -- вдоль малых осей. Локальный максимум у M 31 при $r\approx-40'$ (малая ось) связан со спутником M 31 -- галактикой NGC 205.
\begin{figure}\centerline{\psfig{file=fig5.ps,angle=-90,width=16.5cm}}\end{figure}

Направления большой и малой осей галактики находят по ориентации ее внешних изофот. Эти направления, однако, иногда определяются неуверенно: например, некоторые эллиптические галактики показывают систематическое изменение ориентации изофот, спиральные галактики часто имеют подструктуры, большие оси которых не совпадают с осью по внешним изофотам. Встречаются также случаи, когда разрез вдоль большой (малой) оси галактики плохо характеризует ее структуру (например, на большую ось галактики проектируется пылевая полоса, как в случае NGC 3718).

$\bullet$ Усредненный по азимуту разрез

Это разрез, полученный усреднением распределения яркости $I(a,\phi)$ по $\phi$ вдоль эллипса с большой полуосью $a$ и с видимым сжатием $b/a$. Предполагается, что эллипс является хорошим приближением формы изофот. Этот профиль эффективно сглаживает неосесимметричные неправильности галактики и иногда используется, например, для оценки контраста спиральной структуры. Усредненный по азимуту профиль можно также назвать (и это часто делается) эллиптически-усредненным или усредненным по эллипсу профилем.

$\bullet$ Усредненный в кольцах профиль

Фотометрический профиль галактики на практике часто строят в виде зависимости средней поверхностной яркости в пределах концентрического кольца ($I_m$) от радиуса этого кольца ($r_m$). Построенный таким образом профиль, очевидно, искажает истинное распределение яркости, причем тем сильнее, чем шире используемые кольца. Для того, чтобы уменьшить влияние конечной ширины колец, в [57] было предложено для каждого кольца выбирать соответствующий радиус так, чтобы на этом расстоянии от ядра поверхностная яркость была равна средней в рассматриваемом кольце. Такое определение радиуса зависит от формы распределения яркости в галактике. 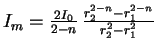В простейшем случае, когда распределение может быть представлено степенным законом $I(r)=I_0\,r^{-n}$, средняя поверхностная яркость в кольце от $r_1$ до $r_2$ согласно [57] равна $I_m=\frac{2I_0}{2-n}\,\frac{r_2^{2-n}-r_1^{2-n}}{r_2^2-r_1^2}$ (исключая случай с $n=2$). Этому значению яркости соответствует радиус кольца $r_m=\left[\frac{2}{2-n}\,\frac{r_2^{2-n}-r_1^{2-n}}{r_2^2-r_1^2}\right]^{-1/n}$. 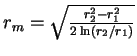При $n=2$ радиус кольца равен $r_m=\sqrt{\frac{r_2^2-r_1^2}{2\,{\rm ln}(r_2/r_1)}}$.

$\bullet$ Эквивалентный профиль

Эквивалентный профиль был введен Вокулером в 1948 году [58]. Если $S$ -- площадь, ограниченная изофотой, то эквивалентный радиус $r^*$ изофоты определяется как радиус круга, имеющего ту же площадь, что и данная изофота: $r^*=\sqrt{S/\pi}$. Зависимость поверхностной яркости от эквивалентного радиуса, соответствующего этой изофоте, называется эквивалентным профилем - $\mu(r^*)$.

Очевидно, что, если изофоты галактики могут быть представлены эллипсами с постоянным сжатием, то эквивалентный профиль должен совпасть с предыдущими. В случае усредненного по эллипсу профиля мы имеем зависимость $\mu(a)$, а эквивалентный профиль -- это $\mu(r^*)$, где $r^*=a\sqrt{b/a}$. Следовательно, при неизменном видимом сжатии изофот галактики -- $b/a$ -- оба профиля будут отличаться на множитель $\sqrt{b/a}$. Например, показанные на рис. 6 профили будут практически совпадать при $b/a=0.8$ [59].

рис.  6: Фотометрические профили спиральной галактики NGC 300 согласно Вокулеру и Пейдж [59]. Непрерывной линией показан усредненный по эллипсу разрез вдоль большой оси, штриховой линией -- эквивалентный профиль.
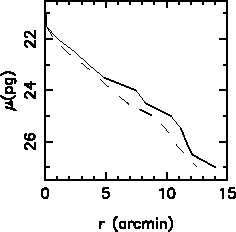\begin{figure}\centerline{\psfig{file=n300.ps,angle=-90}}\end{figure}

Эквивалентный профиль удобен тем, что он позволяет построить сглаженное распределение поверхностной яркости даже для весьма неправильных галактик, изофоты которых сильно нерегулярны и даже состоят из отдельных ``островков'' (рис. 6). В [60] было произведено сравнение результатов анализа глобальной структуры взаимодействующих галактик по их эквивалентным профилям и по разрезам вдоль большой оси. Оказалось, что использование эквивалентных профилей приводит к тем же результатам, что и анализ разрезов.

К недостаткам эквивалентного профиля можно отнести черезчур сильное для ряда задач сглаживание наблюдаемого распределения и чувствительность к геометрии галактики.

$\bullet$ Спроецированный и обобщенный профили

Эти профили были введены в работе [61]. Спроецированный профиль $f(x)$ определяется как проекция наблюдаемого двумерного распределения поверхностной яркости $I_{obs}(x,y)$ на большую ось галактики: $f(x)=\int_{-\infty}^{\infty}I_{obs}(x,y){\rm d}y$, где координата $x$ измеряется вдоль большой оси галактики, а начало координат располагается в ее центре. Если галактика является оптически тонкой и ее наблюдаемая малая ось совпадает в проекции с осью вращения, спроецированный профиль не зависит от наклона галактики к лучу зрения. Тогда спроецированный профиль $f(x)$ связан с обобщенным радиальным профилем $\sigma(r)$ следующим интегральным уравнением: $f(x)=2\int_{\vert x\vert}^{\infty}\frac{\sigma(r)r{\rm d}r}{\sqrt{r^2-x^2}}$. В [61] описана также численная схема для решения этого интегрального уравнения.

Обобщенный профиль удобно использовать для сравнения структуры галактик, имеющих разные наклоны к лучу зрения. При использовании этого профиля следует учитывать, что внутреннее поглощение и неосесимметричность реальных галактик могут привести к появлению на профиле ложных деталей или полностью исказить его. Обобщенные профили, по-видимому, могут быть полезными при инфракрасной фотометрии галактик.

$\bullet$ Профили эллиптичности и ориентации изофот

Изофоты галактики приближаются семейством концентрических эллипсов и строятся зависимости их эллиптичностей $\epsilon=\frac{a-b}{a}$ (или просто сжатий $b/a$) и позиционных углов их больших осей (P.A.) от $a$. Профили эллиптичности и ориентации сглаженных эллипсами изофот используются, например, при исследовании геометрии галактик ранних типов.

рис.  7: Изменение позиционного угла (слева) и сжатия изофоты (справа) в зависимости от большой оси аппроксимирующего изофоту эллипса (в угловых минутах) для эллиптической галактики NGC 3379. Зависимости построены по изображению галактики из DSS.
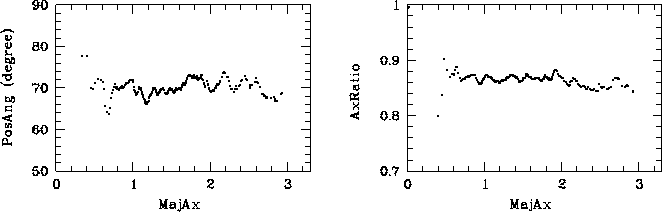\begin{figure}\centerline{\psfig{file=fig6.ps,angle=-90,width=16.0cm}}\end{figure}

На рис. 7 на примере эллиптической галактики NGC 3379 показаны обсуждаемые профили. Видно, что в пределах 0.$'$5-3$'$ от ядра галактики изофоты хорошо аппроксимируются эллипсами с почти постоянными сжатием ($b/a=0.86$) и позиционным углом (P.A.=70$^{\rm o}$) (см. также рис. 4). Эти результаты практически совпадают с данными ПЗС-фотометрии [38], что свидетельствует о том, что изображения галактик из DSS могут быть использованы при исследовании их геометрических характеристик.

$\bullet$ Форма изофот галактики

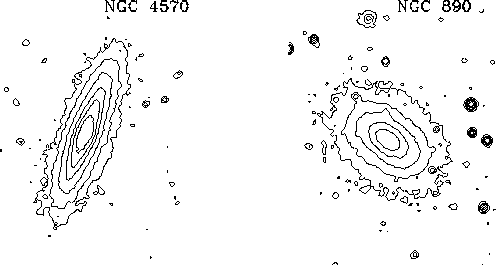
Изофоты галактик, как правило, отличаются от эллипсов. Например, они могут напоминать прямоугольники с закругленными углами, а также они могут быть несколько заострены на концах большой оси. В первом случае говорят о ``ящикоподобных'' изофотах (boxy), во втором -- о ``дископодобных'' (disky). Примеры галактик ранних типов с разными формами изофот показаны на рис. 8. Внешние изофоты NGC 4570 близки к эллипсам, внутренние демонстрируют заострения. У галактики NGC 690 изофоты относятся к ``ящикоподобному'' типу. Дископодобность изофот является свидетельством того, что галактика содержит дисковую составляющую.

рис.  8: Слева -- галактика с дископодобными изофотами, справа -- с ящикоподобными. Изображения извлечены из DSS.
\begin{figure}\centerline{\psfig{file=fig7.ps,angle=-90,width=14.0cm}}\end{figure}

Для количественной характеристики формы изофот обычно используют параметр $a_4$ (см., например, [62,63]). Изофота галактики аппроксимируется эллипсом $R_{ell}(\phi)$ и для каждого угла $\phi$ находится разность между изофотой и эллипсом: $\delta(\phi)=R(\phi)-R_{ell}(\phi)$ (см. рис. 9). Функцию $\delta(\phi)$ можно разложить в ряд Фурье:


\begin{displaymath} \delta(\phi)=\delta_0~+~\Sigma_{n=1}^{\infty}(a_n\,{\rm cos}\,n\phi~+~ b_n\,{\rm sin}\,n\phi). \end{displaymath} (6)

рис.  9: Схема, иллюстрирующая введение параметра $a_4$ формы изофот. Непрерывная кривая изображает реальную изофоту галактики (ящикоподобную), штриховая линия -- ее приближение эллипсом.
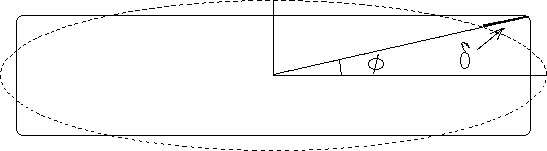
\begin{figure}\centerline{\psfig{file=fig8.ps,width=12.5cm}}\end{figure}

Если рассматриваемая изофота достаточно симметрична, каждая ее четверть подобна остальным и ее форма хорошо аппроксимируется эллипсом, то значения $\delta_0$, $a_1$, $a_2$, $a_3$ и $b_n$ должны быть небольшими. Значение и знак коэффициента $a_4$ будут зависеть от формы изофоты: если изофота имеет дископодобную форму, то $a_4>0$, и $a_4<0$ для ящикоподобной изофоты. Величина коэффициента $a_4$ отражает степень отклонения формы изофоты от эллипса. Для характеристики формы изофот часто используют не сам коэффициент $a_4$, а безразмерный параметр $a_4/a$, где $a$ - большая полуось данной изофоты. Отношение $a_4/a$ называют параметром формы изофот.

Параметр $a_4$ можно ввести и по-другому. Например, аппроксимировав изофоту эллипсом с большой полуосью $a$, можно представить в виде ряда Фурье отклонения интенсивности в галактике вдоль этого эллипса:

\begin{displaymath} I(a,\phi)=I_0(a)~+~\Sigma_{n=1}^{\infty}(A_n(a)\,{\rm cos}\,n\phi~+~ B_n(a)\,{\rm sin}\,n\phi). \end{displaymath} (7)

Тогда коэффициенты отклонения яркости могут быть преобразованы в коэффициенты отклонения формы изофоты через следующие соотношения: $a_n(a)=A_n(a)/{\mid\frac{{\rm d}I(a)}{{\rm d}a}\mid}$ и $b_n(a)=B_n(a)/{\mid\frac{{\rm d}I(a)}{{\rm d}a}\mid}$ (см., например, [24]).

рис.  10: Распределение значения коэффициента $a_4$ вдоль большой полуоси для галактики NGC 4570 согласно [67]. При $r\leq12''$ использованы данные с КТ имени Хаббла, при $r\geq12''$ использованы наземные наблюдения.
\begin{figure}\centerline{\psfig{file=fig9.ps,angle=-90,width=8.0cm}}\end{figure}

Анализ радиального поведения параметра $a_4$ позволяет судить о наличии, относительной светимости и ориентации дисковой подсистемы в сфероидальных звездных системах. Наблюдаемый максимум значения $a_4$ находится примерно на таком расстоянии от ядра, где вклад звездного диска в светимость галактики максимален: $r_{a_4,max}\approx2.4(h^4/r_e)^{1/3}$ ($r_e$ -- эффективный радиус описываемой законом Вокулера галактики (п. 4.1), $h$ -- экспоненциальный масштаб диска (п. 5.1)) [64]. Параметр формы изофот коррелирует с рядом физических свойств эллиптических галактик (например, с их радио- и рентгеновскими характеристиками [65]). Корменди и Бендер [66] даже предложили расширить Хаббловскую классификацию за счет введения двух типов эллиптических галактик: с диско- и ящикоподобными изофотами.

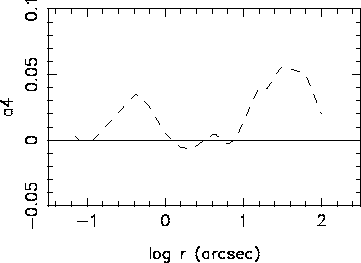
На рис. 10 показана зависимость коэффициента $a_4$ от большой полуоси для E/S0 галактики NGC 4570 (ее изофоты приведены на рис. 8). На рисунке видно, что в околоядерной области (при $r\approx0.''4$) и при $r\approx30''-40''$ коэффициент $a_4$ демонстрирует хорошо выраженные максимумы, связанные с наличием у галактики ядерного и внешнего звездного дисков.

Для более детального анализа формы галактик можно также рассматривать поведение других коэффициентов в разложениях (6) и (7) (см. рис. 1 в [68]).


<< 3. Представление результатов поверхностной | Оглавление | 3.2 Фотометрические параметры >>

Публикации с ключевыми словами: Фотометрическая система - слабые галактики - Скопление галактик - фотометрия
Публикации со словами: Фотометрическая система - слабые галактики - Скопление галактик - фотометрия
См. также:
Все публикации на ту же тему >>

Обсудить эту публикацию
Оценка: 3.1 [голосов: 81]
 
О рейтинге
Версия для печати Распечатать

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце

Астронет | Научная сеть | ГАИШ МГУ | Поиск по МГУ | О проекте | Авторам

Комментарии, вопросы? Пишите: info@astronet.ru или сюда

Rambler's Top100 Яндекс цитирования