|
Гравитационная энергия Чиняков Г.Ю. georg1956@mail.ru
Понятие энергии объясняется, как способность тела совершать какую-то
работу, а знаменитая формула Эйнштейна говорит об эквивалентности массы и энергии.
Напомню, что гравитационная энергия (За которую часто принимают гравитационный потенциал
и по этой величине оценивают гравитационную энергию) определяется: E = - G* M2/ 2
где: G- гравитационная постоянная М-масса
объекта
R-радиус объекта По своему определению
ни какая энергия не может иметь отрицательное значение, тогда необходимо будет признать, что масса может иметь отрицательное значение. В случае с гравитационной энергией
по приведенной выше формуле вычисляется работа тела (или тел) уже выполненная гравитационной энергией, а это не одно и тоже. Иногда хотелось бы узнать, а, сколько гравитационной
энергии осталось? Несмотря, на то, что данная формула позволяет решать большой класс задач, в некоторых случаях она ставит в тупик, либо приводит к парадоксам, что связанно
с неправильным пониманием и применением данного тождества. Поставим задачу определить максимальную гравитационную энергию при взаимодействии двух материальных точек массой
m.
Максимум гравитационной энергии у данной системы, состоящей из двух материальных точек массами m, будет при расстоянии между ними равном бесконечность. При сближении этих точек превращаться
в кинетическую энергию этих тел, которая вычисляется как: Eкин = m* V2/2
Максимальное значение эта энергия может приобрести при скорости близкой к скорости света, которая является пределом. А значит максимальное значение кинетической
энергии данной системы равно:
Emax = m*c2 + m*c2 = M*c2/2
где: М- масса системы с- скорость света Т.к. в данном случае гравитационная энергия может превращаться только
в кинетическую, то и максимальное значение этой энергии для данной системы при расстоянии равном бесконечности тоже не может превышать этой величины. Любителям спецэффектов
теории относительности, поясняю, что в данном случае при приближении к скорости света увеличение сил инерции от роста массы, компенсируется ростом сил гравитации (из-за принципа
эквивалентности) поэтому их можно не учитывать. На любой момент времени, когда тела разделяет расстояние r, гравитационная энергия будут равна: Eгр = M*c2/2 - G*M2/r
Из этой формулы определим, при каком значении r гравитационная энергия равна нулю:
Eграв = 0 отсюда
r = 2GM/c2
т.е. при гравитационном радиусе?! Скорее всего, это объясняется тем, что есть предел, при котором материя в виде вещества
существовать не может. Если радиус звезды (допустим) равен двум гравитационным радиусам, то гравитационная энергия определиться:
Eграв = Mc2/4
Если четырем, то:
Eграв = 3/8Mc2
А так как у большинства звезд радиус значительно больше, то гравитационную энергию можно приблизительно
вычислить по более простой формуле:
E ~ Mc2/2
Т.к. сжатие космических объектов под действием сил тяжести проходит с потерей части массы, то работа сил гравитации по сжатию таких объектов в общем
случае будет определяться:
dEграв = E0 Ek = { M0c2/2 GM02/R0} {Mkc2/2 GMk2/Rk}
Для объектов радиус, которых много больше гравитационного. dEграв ~ d Mc2
∆ М- потерянная масса объекта. Используя такой подход к гравитационной энергии можно решить большое количество проблем в астрономии. Рассмотрим некоторые из них: 1. Эволюция и строение звезд. Предложенная формула гравитационной энергии не запрещает звездам и другим объектам Вселенной иметь сколько угодно большую массу
(что наблюдается часто), т.к. теперь гравитационная энергия пропорциональна массе, в то время как по старой она была пропорциональна квадрату массы, что приводило в противоречие
с наблюдаемыми данными. Эволюция звезд с использованием старой формулы предполагала три типа конечного состояния мертвых звезд: белые карлики, нейтронные звезды, черные
дыры, в зависимости от первоначальной массы. Новая не запрещает эволюционировать звездам из главной последовательности в белый карлик, и потом нейтронную звезду. Это происходит,
по-видимому, при взрыве сверхновых 2-го типа, когда звезда первоначально превращается в белый карлик, и через несколько дней в нейтронную звезду, хотя возможны и другие варианты. 2. К сожалению, для почитателей черных дыр данная формула делает проблематичной существование таких релятивистских объектов, одна из причин: гравитационная
энергия любого тела не превышает энергию необходимую для сжатия вещества до такого состояния. Да и сама природа делает нам подсказку: чем сильнее сжимается объект, тем больше
выделяется энергии. Скорее всего, при достижении гравитационного радиуса, а вернее сказать, критических условий, вещество испариться,
превращаясь в электромагнитное излучение и другие виды материи. В заключение можно сказать, что запас гравитационной энергии можно получить другим путем, а именно интегрированием известной формулы F=Gmm/R2. По R от ∞ до гравитационного радиуса. Знаменитая формула эквивалентности энергии и массы Еэк=mc2 является также
формулой максимальной энергии, которую может иметь система массой m. Итак полная энергия любого тела равна Епол=Еэкв=Мс2 , почти
половина из которой гравитационная.
| 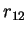 ,
,