§ 7.4 Численное моделирование эволюции звездных скоплений
Развитие вычислительной техники дало возможность поставить задачу о непосредственном численном эксперименте с моделью звездной системы, состоящей из большого числа материальных точек, взаимодействующих между собой по закону Ньютона. Решение этой задачи в принципе заключается в прямом численном решении системы (7.1) при некоторых заданных граничных условиях. Таким путем можно проследить эволюцию звездной системы, получить такую ее характеристику, как распределение концентрации звезд внутри системы, определить число вылетевших звезд. Наконец, в принципе можно было бы изучить поведение звездной системы в зависимости от выбора начальных условий.
К сожалению, практическое выполнение этой программы наталкивается на много трудностей. Прежде всего следует отметить, что объем вычислений очень быстро растет с увеличением числа звезд N, примерно как N4. Правда, есть специальные методы, упрощающие счет, но приводящие к потере точности и общности.
Поэтому первые работы рассматривали скопления из небольшого числа звезд. В работах Хорнера [17] рассматривались звездные скопления, состоящие из 16 и 25 звезд (см. также [18]). Путем численного решения системы (7.1) определялось распределение концентрации звезд в зависимости от расстояния r до центра скопления, установившееся через несколько времен релаксации. В этих работах эффект вылета звезд из скоплений специально не изучался. В работах [17, 18] на основании численных экспериментов, а также аналитических оценок, было получено, что по истечении нескольких времен релаксации в звездном скоплении образуется более плотное сжимающееся ядро с распределением концентрации звезд n ∼ r-12/5 и относительно протяженное гало с распределением n ∼ r-15/4. В этих расчетах также получилось, что примерно за 20 времен релаксации (при N = 25) ядро становится очень плотным - теоретически стремится к бесконечности как n ∼ (t-t0)-4/3, а из численного эксперимента получилось n ∼ (t-t0)-1.5. где t0 - некоторое характерное время коллапса ядра. При этом ядро теряет звезды как Nяд ∼ (t-t0)1/3. В численных расчетах принималось, что эволюция скопления заканчивалась, когда в ядре скопления оставалось три звезды.
В работе [18] Хорнер прослеживает эволюцию ядра скоплений вплоть до момента времени, когда звезды начинают сталкиваться, т. е. тогда, когда нужно учитывать и конечный радиус звезды. Столкновение звезд в плотных ядрах галактик привлекалось для объяснения явлений квазаров.
Важным этапом в развитии численного моделирования систем была программа, проведенная по инициативе Лекара [19]. Суть этой программы заключалась в следующем.
Рассматривается звездное скопление из 25 звезд одинаковой массы. Задаются начальные координаты звезд в скоплении (с 16 значащими цифрами). Начальные скорости равны нулю. Тем самым определяется начальная потенциальная энергия скопления. Далее по системе уравнений (7.1) рассчитывается дальнейшая эволюция скопления. Смысл всей программы был в том, чтобы на различных ЭВМ в разных институтах по своим программам рассчитывалась бы эволюция одного п того же скопления с одними и теми же начальными условиями. Сравнение полученных результатов позволяет судить, насколько однозначны выводы, полученные из численных экспериментов со звездными скоплениями. В работе [19] и проводится такое сопоставление.
Численно решалась безразмерная система (7.12) при Π = 1, qi = 1, N = 25. В безразмерных единицах начальная потенциальная энергия скопления U = -0.2. Эта величина должна оставаться и полной энергией скопления Е до тех пор, пока вылеты звезд ее не изменят. Характерное время пересечения
|
|
(7.59) |
в безразмерных единицах равно 4. Время релаксации (7.32) в безразмерных единицах равно 2,5 (в [19] использована другая формула для времени релаксации, отличающаяся от (7.32) заменой 12 в знаменателе на 2 π, так что там принято время релаксации равным 4,9).
В начальном состоянии все скопление имеет радиус 2,75 в безразмерных единицах.
По стандартной программе Лекара было проведено 11 независимых расчетов. Результаты их таковы. Вначале имеет место коллапс скопления. За время τ = 5,4 в безразмерных единицах (т. е. за 1,6 времен пересечения) радиус скопления уменьшается до 1,25, т. е. средняя плотность растет в 10,6 раза. При этом образуется центральное плотное ядро. Плотность сферы, содержащей 10 ближайших к центру звезд, увеличивается в 345 раз. Такой начальный коллапс скопления получился более или менее одинаковым во всех независимых расчетах. Но последующая эволюция скопления оказалась очень различной в разных расчетах.
На рис. 27 показан ход вириального коэффициента, т. е. отношения удвоенной кинетической энергии к потенциальной энергии скопления
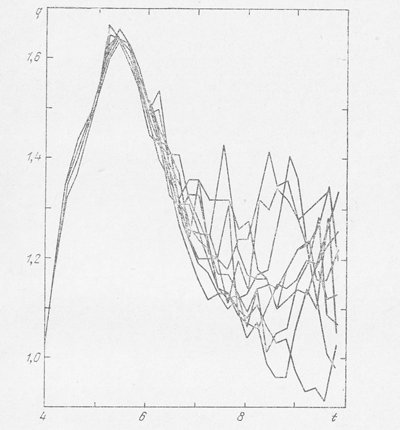
Рис. 27. Изменение со временем вириального коэффициента (7.60) в стандартной задаче 25 тел.
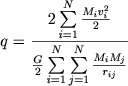
|
(7.60) |
в зависимости от времени. Сразу видно, что если начальный коллапс протекает одинаково во всех расчетах, то последующее расширение (уменьшение q), а затем и пульсации звездного скопления различаются в разных расчетах более чем вдвое. Заметим, что в квазиравновесном состоянии вириальный коэффициент должен быть близок к единице.
Средние значения дисперсии радиальных и тангенциальных компонент скорости в безразмерных единицах даны на рис. 28. Здесь также имеется большой разброс значений. Следует еще 'Отметить, что мгновенные значения дисперсий скоростей заметно флуктуируют с течением времени, но средние по времени дисперсии более или менее постоянны.
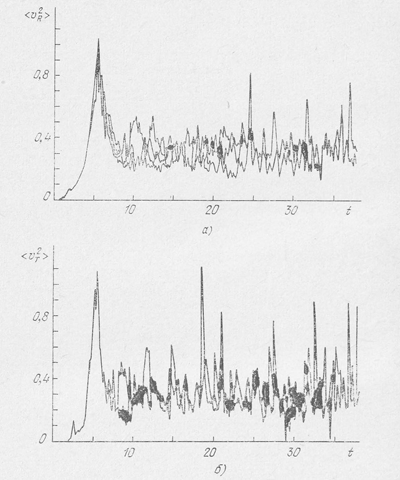
Рис. 28.
Особое внимание в работе Лекара уделялось анализу процесса вылета звезд из скопления. К сожалению, и здесь разные расчеты давали различное число вылетевших звезд - от 1 до 5. Если усреднить результаты всех расчетов, то за время, равное двум характерным временам релаксации, отсчитываемым от начала расчета, скопление потеряло три звезды или 6% от полного числа звезд за одно время релаксации. Эта величина на порядок больше, чем следует из теории (0,74%). Надо также отметить, что в разных расчетах вылетали разные звезды и не было ни одного случая, чтобы одна конкретная звезда вылетела бы в каждом расчете. Чаще всего вылетала конкретная звезда за номером 25 (в восьми расчетах из 11), звезды за номерами 18 и 6 вылетели в шеспи расчетах из 11. Есть звезды, которые вылетели только в одном из 11 расчетов.
Объяснение всех этих расхождений, по крайней мере отчасти, может быть связано с выбором начальных условий, приводящих к быстрому коллапсу скопления. В самом деле, сразу же после начала счета из-за нулевых начальных скоростей скопление быстро сжимается и скорости звезд столь же быстро увеличиваются. Это и отражается на резком увеличении вириального коэффициента. Быстрое увеличение скоростей звезд делает более вероятным вылет звезд из скоплений. Кроме того, уплотнение скопления яа начальном этапе увеличивает обмен энергией между звездами, что также повышает вероятность вылета звезд. Наконец, резкое изменение состояния скопления на начальном этапе, по-видимому, увеличивает и ошибки счета. Для получения более согласованных результатов следовало бы повторить подобную программу одновременного расчета, но с другим выбором начального состояния так, чтобы избежать этого коллапса.
Очень серьезной трудностью численного эксперимента в проблеме N гравитирующих тел является то, что в уравнениях системы (7.1) имеются особые точки rij → 0. При сближениях любой пары звезд соответствующий член в уравнениях (7.1) быстро растет. Это в свою очередь быстро увеличивает ошибки счета. Для сохранения точности приходится уменьшать шаг счета как по координате, так и по времени. Это замедляет численное интегрирование и приводит к большей неоднозначности. Указанный эффект также объясняет расходимость результатов счета в стандартной проблеме 25 тел.
Выходом из этого затруднения может быть модификация потенциала гравитационного взаимодействия на малых расстояниях. В частности, в работе В. И. Алешина и С. А. Каплаяа [20] вместо обычного выражения для потенциальной энергии звезд вида GMiMj / rij было принято выражение
|
|
(7.61) |
где ε - некоторая постоянная, выбранная из соображений удобства счета. Некоторые физические соображения в пользу такого выбора обсуждаются в работе [20]. Здесь же заметим, что использование потенциала (7.61) уменьшает вероятность тесных сближений, а следовательно, и начальное сжатие.
В работе [20] было проведено численное .моделирование эволюции скопления из 25 тел при тех же начальных условиях, что и в стандартной программе Лекара. Благодаря отсутствию тесных сближений расчет эволюции скопления можно провести гораздо дальше по времени. Если в обычной программе Лекара наиболее длинный расчет занимал 10 времен пересечений, то в расчете [20] была прослежена эволюция скопления за 30 времен пересечений. Результаты расчета [20] в общем согласуются с расчетами [19]. Это показывает, что замена действительного потенциала гравитационного взаимодействия на выражение (7.61) не приводит к кардинальным изменениям. На рис. 29 приведен ход вириалшого коэффициента. Существенных отличий от рис. 27 нет.
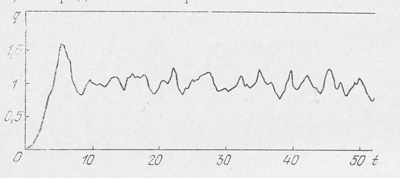
Рис. 29. Вириальный коэффициент в задаче 25 тел с потенциалом взаимодествия, имеющим вид (7.61)
На рис. 30 приведены дисперсия радиальных и тангенциальных компонент скоростей звезд. В принципе этот рисунок мало отличается от рис. 28. Здесь также тангенциальные скорости показывают большие флуктуации, чем радиальные скорости.
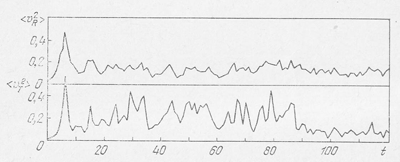
Рис. 30. Дисперсия радиальных (вверху) и тангенциальных (внизу) скоростей звезд в задаче 25 тел с потенциалом взаимодествия, имеющим вид (7.61)
В расчете [20] на стадии, непосредственно следующей за первоначальным коллапсом, вылетало две звезды, в том числе за номером 25, т. е. та звезда, которая чаще всего вылетала и в расчетах [19]. Все это происходило за первые два времени релаксации. В течение последующих примерно 20 времен релаксацией вылетало три звезды. Следовательно, за одно время релаксации квазистационарного состояния вылетаегт 0,6% от полного числа звезд. Это уже ближе к теоретическим оценкам. Получившееся даже более низкое, чем в теории, значение легко объяснить тем, что введение параметра к в (7.61) заметно уменьшает вероятность сближений, а следовательно, и возможность приобретения больших скоростей звездами скопления.
Теперь рассмотрим работы, посвященные численному моделированию звездных скоплений с большим числом звезд (N ≈100-250).
Аарсет [21] исследовал эволюцию скопления из 250 звезд методом численного эксперимента, используя выражение для потенциальной энергии гравитационного взаимодействия двух звезд в виде
|
|
(7.62) |
где ε - также некоторая постоянная величина. Другое отличие этой работы от описанных выше в том, что здесь предполагалось различие масс звезд. Использована следующая функция распределения звезд по массам (табл. 12):

Таблица 12
Расчет эволюции такого скопления был прослежен в течение 28 времен пересечения. Существенной особенностью эволюции этого скопления является образование двойных систем, например, две самые тяжелые звезды с массами 25 единиц быстро образуют двойную систему в центре скопления. Существование этой пары сильно меняет весь характер эволюции, в частности, приводит к более быстрому вылету звезд из скопления.
В результате эволюции в скоплении устанавливается некоторое квазиравновесное распределение концентрации звезд в зависимости от расстояния до центра скопления. Относительное уменьшение звезд в центральной области- скопления объясняется большой ролью вылета звезд из этой области, также обязанной влиянию центральной массивной пары. В среднем по скоплению n ∼ r-3, во внешней части (гало) лучше подходит зависимость n ∼ r-4, что в общем хорошо согласуется с результатами [18]
В работе [21] подробно изучалась я основная задача численного эксперимента со скоплениями - определение числа вылетевших звезд за одно время релаксации. Результаты численного эксперимента [21] показали, что в среднем за одно время релаксации вылетает 3,4% полного числа звезд. Определена также зависимость звезд от их массы. В частности, за одно время релаксации вылетает 2,5% от числа звезд самых малых масс. Интересно, что если за первую половину просчитанного времени эволюции вылетело 44 звезды, то за вторую половину этого времени вылетело всего 24 звезды. Начальная быстрая потеря звезд может быть объяснена сжатием скопления, затем значительное число звезд вылетает в то время, когда образовавшаяся в центре скопления пара звезд с массами в 25 единиц еще имеет большое расстояние между компонентами. Отдавая энергию другим звездам скопления, эта пара становится более тесной, а те звезды, с которыми эта пара взаимодействует, получив большую энергию, вылетают из скопления. После того как центральная тяжелая пара становится достаточно тесной, ее взаимодействие с остальными звездами становится менее эффективным и вылет звезд замедляется. Экстраполяция расчетов показывает, что скопление должно потерять половину звезд примерно за 60 периодов пересечения.
Как уже отмечалось, в данном численном эксперименте получилась слишком большая скорость вылета звезд по сравнению с теоретическим расчетом (3,4% вместо 0,74%). Анализ численного счета показывает, что из 68 вылетевших звезд 45 приобрели параболическую скорость непосредственно вблизи центральной пары, еще 16 звезд ускорились в районе центрального ядра (при г < 1).. Это означает, что процесс вылета звезд в данном случае определяется главным образом тяжелой центральной парой и поэтому полученное высокое значение для скорости вылета нетипично для скопления без таких центральных пар.
Проблема вылета звезд из скопления на основе метода численного интегрирования рассматривалась также Виленом [22]. Изучалась эволюция скопления из 100 звезд, но рассматривались разные модели. Во всех моделях, кроме одной, учитывалась неодинаковость масс со следующей функцией распределения (табл. 13)

Таблица 13
Предполагались различные начальные условия, учитывалось вращение скопления и влияние внешнего гравитационного поля галактики. В этой работе решалась система уравнений (7.1) в ее чистом виде (т. е. с потенциалом, имеющим особенности при rij → 0), и поэтому эволюция каждой модели была прослежена всего на 5-12 времен пересечения. Чтобы получить более уверенные статистические данные о вылете звезд, в работе суммировалось время эволюции моделей. Например, в трех моделях с разными массами звезд за суммарное время эволюции, равное 30 временам пересечения, вылетело 23 звезды. Это значение более или менее соответствует теоретическим оценкам [3, 6, 7]. Однако расчет модели с равными массами при прочих одинаковых условиях, прослеженный на 9,6 времен пересечения, не привел к вылету хотя бы одной звезды. Экстраполируя данные о модели с разными массами и учитывая теоретические оценки, можно было бы ожидать, что за это время вылетит семь звезд. Вероятность того, что случайно не вылетело ни одной звезды, очень мала, всего около 6 × 10-4
Другое расхождение с теорией связано с распределением вылетевших звезд по массам. Теоретически звезды малых масс вылетают заметно чаще, чем звезды средних масс, а в численном эксперименте [22] получилось, что распределение вылетевших звезд по массам примерно соответствует их распределению в самом скоплении. Например, звезд с массой 0,55 в модели скопления в 2,6 раза больше, чем звезд со средней массой 1,1; вылетело звезд с малой массой в 2,5 раза больше, чем звезд со средней массой, а теоретически скопление должно потерять звезд с массой 0,55 примерно в 15 раз больше, чем звезд с массой 1,1.
В работе [22] обсуждаются причины таких расхождений с теорией, но надо отметить, что и теоретические оценки числа и распределения масс вылетевших звезд также неоднозначны. Автор работы [22] считает, что его результаты лучше согласуются с работой [8]. В работе [22] рассматривался также случай, когда в процессе эволюции две самые массивные звезды (с массами 4,4) внезапно теряли свою массу и превращались в малые звезды с массами 0,55. Это приводило к заметному ускорению вылета звезд.
Приведем количественные результаты. Рассматривалось скопление, которое за первые 10 времен пересечений, пока массы звезд 4,4 оставались неизменными, потеряло шесть звезд. Затем сразу же после внезапного уменьшения массы двух тяжелых звезд это скопление практически мгновенно потеряло еще три звезды, а за последующие пять времен пересечений оно потеряло еще семь звезд.
Результаты численного эксперимента Видена [22] наглядно показывают, что еще много предстоит выяснить с целью согласования теории и численного эксперимента.
Как уже отмечалось, основной причиной ошибок счета и главной трудностью в построении численных моделей звездных скоплений 'являются особые точки в уравнениях системы (7.1), появляющиеся при rij → 0, т. е. при тесных сближениях звезд. Для преодоления этой трудности в численных расчетах еще в 1903 г. Леви-Чивита предложил метод регуляризации. Этот метод был обобщен Кустанхеймо и Штифелем [23], а применительно к звездным скоплениям метод обсуждался в [24 - 26]. Метод регуляризации удобнее пояснить на примере одномерного движения (лобового столкновения двух материальных точек). Здесь уравнение движения:
|
|
(7.63) |
где х - расстояние между точками и М - приведенная масса. Из (7.63) следует интеграл энергии
|
|
(7.64) |
где W - полная энерпия, отнесенная к единице массы. При численном решении (7.63) с заданной точностью приходится все время уменьшать шаг по времени по мере уменьшения x, и при x → 0 шаг по времени становится бесконечно малым. Для того чтобы избежать этого, в методе Леви-Чивита вводится редуцированное время τ,
|
|
(7.65) |
с тем, чтобы одновременное уменьшение шага по t и x оставляло шаг по τ конечным. С заменой (7.65) уравнения (7.63) и (7.64) приобретут вид
|
|
(7.66) |
|
|
(7.67) |
Здесь уже нет особенности в нулевой точке, и численное интегрирование (7.66) проводится без затруднений. Собственно, нетрудно получить и аналитическое решение (7.66), но наша цель - показать, как устраняется особенность.
Обобщение Кустанхеймо и Штифеля на трехмерный случай заключается во введении не только редуцированного времени
|
|
(7.68) |
но и редуцированных координат u1, u2, u3 и u4.
|
|
|
|
|
|
|
|
(7.69) |
В переменных (7.68) - (7.69) система уравнений для трехмерного движения двух тел имеет вид
|
|
(7.70) |
где W - по-прежнему величина полной энергии относительного движения, рассчитанная на единицу массы. В старых и новых переменных
![$$
W = \frac{1}{2} \left( \frac{dr}{dt} \right)^{2} - \frac{GM}{r} = \frac{1}{r} \left[ 2 \sum\limits_{i=1}^{4} \left( \frac{du_{i}}{d \tau} \right)^{2} -GM \right]
$$](https://images.astronet.ru/pubd/2013/03/01/0001281314/tex/formula32.gif)
|
(7.71) |
Система (7.70) также не имеет особенностей в нулевой точке и не представляет трудностей для численного интегрирования.
Наконец, обобщение метода регуляризации на случай задачи многих тел сводится к введению редуцированного времени по формуле
|
|
(7.72) |
где, по-прежнему, rij - расстояние между звездами Mi, Mj. Редуцированные координаты вводятся аналогично (7.69)
Здесь также исчезают особенности в нулевых точках, но система уравнений движения звезд в скоплениях становится очень громоздкой. Возможно именно поэтому описанный метод регуляризации еще не нашел широкого применения в численных экспериментах со звездными скоплениями. Чаще все же употребляются простые видоизменения потенциала гравитационного взаимодействия (7.61) или (7.62).
Другой упрощенный метод численного эксперимента со звездными скоплениями предложили Т. А. Агекян и А. С. Баранов [27, 28]. В этом методе уравнения системы (7.1) решаются для небольшого числа звезд, например, для N = 5. Затем средняя концентрация звезд в скоплении в некотором объеме на заданном расстоянии от центра определяется для времени, проводимого всеми звездами в этом объеме. Каждая из N звезд побывает в каждом данном объеме много раз и если время счета достаточно велико, то определенная подобным образом средняя концентрация статистически достоверна. Таким же образом можно определить и средние скорости и дисперсии скоростей. Разумеется, этот метод не позволяет изучать вылет звезд из скопления, хотя и здесь для оценок можно определить долю времени, проводимого звездами на далеких расстояниях от скопления. Этим методом в работах [27, 28] .исследованы структура и распределение скоростей в квазистационарных скоплениях звезд с одинаковыми и разными массами. При решении системы (7.1) принято N = 5.
В заключение этого параграфа отметим, что в работах [29, 30] рассматривался численный эксперимент со скоплениями гравитирующих по закону Ньютона тел, но с учетом изменения их масс. В работе [29] предполагалось, что система тел погружена в плотное тазо-пылевое облако и что имеет место аккреция вещества на эти тела. Определялись функции распределения масс. Результаты численного эксперимента показали, что медленные звезды скопления быстрее набирают массу, что в свою очередь приводит к еще большему их замедлению и к еще более быстрому росту массы. Это означает, что в подобных скоплениях звезд с аккрецией более вероятно образование небольшого числа звезд с большей массой, чем равнораспределение массы по большему числу звезд.
В работе [30] методом численного эксперимента рассмотрено скопление большого числа тел, движущихся под действием взаимного гравитационного притяжения и оказавшихся вблизи друг от друга. Такой расчет может моделировать образование планет и их спутников из протопланетной среды. Здесь также оказалось, что происходит преимущественное образование одного или нескольких тел большой массы, у которых могут оказаться захваченными спутники -тела, оставшиеся с малой массой.
<< § 7.3 Волны плотности во вращающихся галактиках | Оглавление | § 7.5 Численное моделирование плоских вращающихся галактик >>