|
по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу |
Звездные скопления
<< 7.4 Пространственно-кинематические характеристики звездных скоплений и эволюция Галактики | Оглавление | 8.2 Аналитические и численные методы анализа радиального распределения пространственной звездной плотности в скоплениях >>
Глава 8. Строение и размеры звездных скоплений
"И тогда я открыл свою книгу в большом
переплете,
Где на первой странице растения виден
чертеж.
И черна и мертва, протянулась от книги
к природе
То ли правда цветка, то ли в нем заключенная
ложь.
И цветок с удивленьем смотрел на свое
отраженье
И как будто пытался чужую премудрость
понять."
Н. Заболоцкий, Все, что было в душе...
8.1 Видимое распределение звезд в скоплениях. Методы анализа отклонений формы шаровых скоплений от сферической
Большенство шаровых скоплений в проекции на плоскocть, касательную к небесной сфере, имеет эллиптическую форму. Кто означает, что их реальная пространственная форма отклоняется от сферической. Обычно принимают, что шаровые скопления являются сфероидами, т. е. сплюснутыми, а не вытянутыми, эллипсоидами вращения. В дальнейшем мы тоже будем придерживаться этой точки зрения. Однако, поскольку шаровые скопления движутся в общем силовом поле Галактики, нельзя не считаться с возможностью их деформации внешними, например, приливными силами.
Методы анализа отклонений формы шаровых скоплений от сферической совершенствовались постепенно. Первую попытку в этом направлении сделал Бэйли (1916), подсчитавший для 10 скоплений числа звезд в восьми 45-градусных секторах с вершинами в центре скопления. Нанесение этих чисел как ординат против наименований соответствующих секторов, расположенных в порядке возрастания позиционных углов, давало представление о распределении звезд в данном скоплении в зависимости от направления от его центра. Этот способ анализа широко использовался затем Шепли (1930), интерпретировавшим синусоидальную волну на подобном графике как индикатор эллиптичности данного скопления.
Позднее Шевалье (1918), а также X. Шепли и М. Шепли (1919) ввели в употребление полярную диаграмму, на которой по радиусам-векторам откладываются отрезки, пропорциональные числам звезд в соответствующих секторах; концы отрезков последовательно соединяются между собою. Для исследования эллиптичности на разных расстояниях от центра скопления рассматривались числа звезд в последовательных кольцевых зонах различных секторов. Описанные способы позволяли определять направления больших осей эллипсов, но оценка степени эллиптичности оставалась в них чисто качественной. В той же работе X. Шепли и М. Шепли (1919), изучившие эллиптичность 41 шарового скопления, нашли, что непосредственные оценки вида скоплений, па мелкомасштабных снимках, подобных картам Франклин-Адамса, позволяют найти направление большой оси скопления так же определенно, как и подсчеты.
В работе Шепли и Сойер (1927б) степень эллиптичности характеризуется уже более наглядно - десятикратным отношением малой оси b эллипса фотографического изображения скопления к его большой оси а. Эту величину авторы называют эллиптичностью, хотя обычно под эллиптичностью или сжатием понимают величину (а - b)/а Шепли и Сойер приводят оценки эллиптичности 75 шаровых скоплений, но позиционные углы больших осей были определены ими лишь для 37 из них.
Фройндлих и Хейсканен (1923) предложили первый аналитический метод исследования эллиптичности шаровых скоплений, основанный на определении элементов эллипса инерции проекции скопления на небесную сферу. Если звезды скопления в проекции распределены эллиптично, то момент инерции их системы относительно некоторой оси, проходящей в плоскости проекции через центр масс системы (отождествляемый обычно с центром скопления), который равен сумме квадратов расстояний членов скопления от этой оси, будет меняться с изменением направления последней, достигая максимума относительно направления малой оси эллипса проекции скопления и минимума - относительно оси, совпадающей с большой осью эллипса проекции.
Вводя определенные допущения о распределении звезд, можно найти не только направление большой оси эллипса распределения, но и отношение его осей. Однако этот способ анализа мало нагляден и не позволяет анализировать сплюснутость эллипсов на разных расстояниях от центра системы. Он не позволяет также выявить асимметрию системы.
Бруггенкате (1927) в своей монографии развил метод для точного аналитического определения элементов эллипса проекции скопления на небесную сферу. Скопление делится на ряд (n) секторов. В каждом секторе строится соответствующая кривая видимой плотности F(r), показывающая изменение этой плотности с изменением расстояния r от центра системы. Граница скопления в данном направлении определяется значением r, при котором кривая F(r) переходит в плотность звезд фона F0. Вместо этой неуверенной границы можно определять кривую, соответствующую некоторой постоянной видимой плотности F'0, слегка превышающей F0. Эта кривая принимается за эллипс с центром, совпадающим с центром скопления. Бруггенкате пишет уравнение эллипса в прямоугольных координатах в виде
|
(8.1) |
Решая по способу наименьших квадратов систему n таких уравнений, составленную по известным координатам n точек рассматриваемого эллипса, находят коэффициенты A, B и С, по которым затем можно найти полуоси а и b эллипса, эксцентриситет эллипса 
и позиционный угол φ его большой полуоси а.
Бруггенкате применил этот метод для определения ориентации внешних частей восьми скоплений, для которых Пиз и Шепли (1917) опубликовали подсчеты большого числа звезд в находящихся на разных расстояниях от центров скоплений отрезках тридцатиградусных секторов.
Тогда же Кинле (1927), использовав подсчеты Пиза и Шепли в их неопубликованном первоначальном виде (числа звезд в квадратах прямоугольной сетки, наложенной на негатив), впервые опубликовал рисунки кривых равной видимой плотности на разных расстояниях от центра для пяти шаровых скоплений. Однако Кинле не определял элементы эллипсов, аппроксимирующих эти кривые, а ограничился чисто качественными заключениями, так как его интересовали не плавные эллипсообразные кривые, а неправильности на них, которые он интерпретировал как следы спиральной структуры в скоплениях или признаки истечения из них звезд.
Через два года появилась работа Хекмана и Зидентопфа (1929), критикующая выводы Кинле и объясняющая неправильности в кривых постоянной видимой плотности случайными колебаниями подсчетов. Вопрос о признаках спиральной структуры в звездных скоплениях, дискутировавшийся в 20-х годах (см., например, Бруггенкате, 1927, с. 63-68), с тех пор серьезно не возникал, хотя отдельные исследователи время от времени обращают внимание на случайные конфигурации звезд в скоплениях, напоминающие спирали.
В 1928 г. Схилт (1928) на примере скопления ω Cen показал возможность анализа эллиптичности шаровых скоплений на основании измерений распределения интенсивности излучения в их внефокальных изображениях. Эксцентриситеты эллипсов равной плотности в ω Cen уменьшались по мере приближения к центру скопления. Денситометрические измерения диаметров 70 шаровых скоплений, которые провели Шепли и Сэйер (1935), также показали заметные изменения сплюснутости некоторых скоплений с изменением расстояния от их центра.
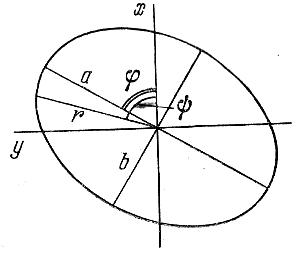
Рис. 115. Схема, поясняющая вывод формул (8.2) и (8.3).
В 1952 г. Холопов (1953а) обработал все опубликованные данные о подсчетах звезд в двадцати шаровых скоплениях по методу, близкому к методу Бруггенкате, определив элементы эллипсов равной видимой плотности звезд разных типов на разных расстояниях от центров рассмотренных скоплений, пользуясь уравнением эллипса, записанным в полярных координатах (рис. 115):
|
(8.2) |
|
(8.3) |
Определив значения А, В, С путем решения по способу наименьших квадратов системы условных уравнений вида (8.2), нетрудно отсюда найти элементы эллипса а, b, φ.
В результате выяснилось, что в шаровых скоплениях, как правило, не существует единой ориентации больших осей кривых постоянной видимой плотности и единых отношений их полуосей η = b/а для подсистем звезд разных типов и для разных расстояний r от центра рассматриваемого скопления. Отношение η заключено в пределах 0,6 ≤ η ≤ 1,0, причем оно может расти и убывать с изменением r.
В некоторых скоплениях, как, например, в М3, М5, М15, некоторые подсистемы входящих в них звезд показывают поворот больших осей эллипсов равной плотности с переходом к менее плотным частям скоплений. Этот поворот происходит, пo-видимому, не постепенно, а скорее скачком, характеризуя переход от одной физически однородной области скопления к другой. Различия в видимом распределении звездной плотности, наблюдаемые при переходе от более плотных центральных областей к менее плотным внешним, очевидно, соответствуют аналогичным реальным различиям в распределении пространственной плотности.
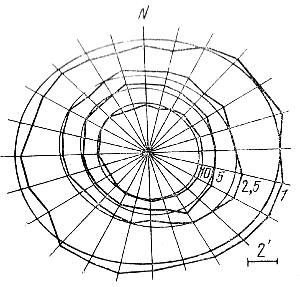
Рис. 116. Кривые равной видимой плотности звезд ярче 16m,8 pv скопления М 3. Числа, стоящие рядом с кривыми, соответствуют числам звезд в 1 кв. минуте дуги.
Для иллюстрации сказанного на рис. 116 приведены кривые paвной видимой плотности ярких звезд скопления МЗ (включая звезды ветви красных гигантов, горизонтальной ветви и верхней части последовательности субгигантов).
Отмеченные выше у некоторых шаровых скоплений факты поворота осей эллипсов равной плотности и изменения отношения их полуосей с расстоянием от центра сходны с явлениями, отмеченными Ивэнсом (1951) у некоторых эллиптических галактик. Поскольку в динамическом отношении шаровые скопления и эллиптические галактики должны быть весьма сходны, то не удивительно, что оба типа объектов обнаруживают сходные явления.
После открытия у изображений ряда шаровых скоплений определенной ориентации на небесной сфере различные авторы (X. Шепли, М. Шепли, 1919; Бруггенка-те, 1927; Шепли, Сойер, 1927б; Джонсон, 1952) безуспешно пытались связать эту ориентацию с какой-либо преимущественной ориентацией осей или плоскостей симметрии рассматриваемых систем в пространстве и установить закономерности изменения их по отношению к плоскости или центру Галактики.
Можно думать, что всякие попытки искать признаки преимущественной ориентации шаровых скоплений по ориентации их внутренних частей (а данные, использованные авторами упомянутых выше работ, относятся именно к "главным телам", или ядрам, скоплений) обречены на неудачу в связи с возможным различием ориентации внутренних, промежуточных и внешних частей скоплений. Скорее можно было бы рассчитывать заметить влияние внешних возмущений на внешние области подсистем более слабых звезд шаровых скоплений. Однако наши данные свидетельствуют об отсутствии роста эллиптичности подсистем слабых звезд с удалением от центров скоплений.
Анализ видимого распределения звездной плотности в рассеянных скоплениях дает менее уверенные результаты в связи с меньшим количеством звезд в этих системах и большим влиянием звезд фона на результаты подсчетов.
С 1966 г. для исследования эллиптичности шаровых скоплений с успехом применяется так называемый метод эквиденсит, основанный на использовании явления соляризации при надлежащей обработке фотоэмульсий, позволяющей выделять на изображении тонкие линии равной плотности (Кадла, 1966б; Систеро, Фуркад, 1970; Хогнер и др., 1972; Кадла и др., 1977).
<< 7.4 Пространственно-кинематические характеристики звездных скоплений и эволюция Галактики | Оглавление | 8.2 Аналитические и численные методы анализа радиального распределения пространственной звездной плотности в скоплениях >>
|
Публикации с ключевыми словами:
звезды - Скопление
Публикации со словами: звезды - Скопление | |
См. также:
Все публикации на ту же тему >> | |
