6.4 Проблема определения расстояний до шаровых скоплений. Проблема субкарликов
При определении расстояний до шаровых скоплений с помощью главных последовательностей этих систем мы, очевидно, сталкиваемся с теми же проблемами, которые уже были рассмотрены ранее в §§ 3.11-3.15 в связи с определением расстояний до скоплений рассеянных. Это проблемы учета эволюционных эффектов, учета различий в содержании тяжелых элементов (а также, возможно, и гелия) и определения начальной главной последовательности для звезд с малым содержанием металлов.
После того как было выяснено, что начальная главная последовательность звезд с низким содержанием металлов на диаграмме MV, В - V после учета покровного эффекта должна совпасть с начальной главной последовательностью звезд с высоким содержанием металлов (последовательностью Гиад), вопрос о выборе начальной главной последовательности звезд шаровых скоплений считался решенным. Для совмещения с нею главных последовательностей шаровых скоплений (после внесения в них поправок зa покровный эффект) оставалось учесть изменение ее формы, обусловленное эволюционными эффектами.
В § 3.11 описан метод Джонсона (1960) определения расстояний до рассеянных скоплений, основанный па использовании кривой эволюционных отклонений. Там же изложены результаты применения этого метода Сэндиджем (1962а) для нахождения расстояний до очень старых рассеянных скоплений. После всего сказанного ясно, что таким же образом можно определять расстояния и до щаровых скоплений. Следует учесть только, что в последнем случае нужно пользоваться не кривой эволюционных отклонений для звезд "типа I" (см. табл. 3.5), а кривой эволюционных отклонений для звезд "типа IIа" (X = 0,99, Y = 0,009) или "IIb" (X = 0,75, Y = 0,249), так как формы этих кривых различны.
Используя кривую эволюционных отклонений для звезд "типа IIa" Сэндидж (1962а, б) определил расстояния до шаровых скоплений M 3, M 5, M13, считая, что избытки цвета этих систем равны нулю. Па рис. 86 (Сэндидж, (1962а) показано расположение основных последовательностей этих скоплений и старых рассеянных скоплений М 67 и NGC 188 на диаграмме MVc, (В - V)c, где индекс с означает, что соответствующие величины исправлены за покровный эффект. Но здесь мы должны обратить внимание на то, что нанесенное на рис. 85 сплошной линией положение главной последовательности Гиад основано на принимавшемся Эггеном и Сэндиджем (1962) значении модуля расстояния Гиад 3m,1. Увеличивая это значение на 0m,2 (см. § 3.14), следует признать, что учет покровного эффекта не может привести положения "экстремальных" субкарликов на рис. 85 на новую начальную главную последовательность звезд с высоким содержанием металлов (см. § 3.15), изображенную на рис. 85, б прерывистой линией, даже если допустить (Эгген, 1971в; 1973), что эти субкарлики за время существования Галактики заметно проэволюционировали и сместились на диаграмме MV, В - V - вправо за счет эволюционных эффектов.
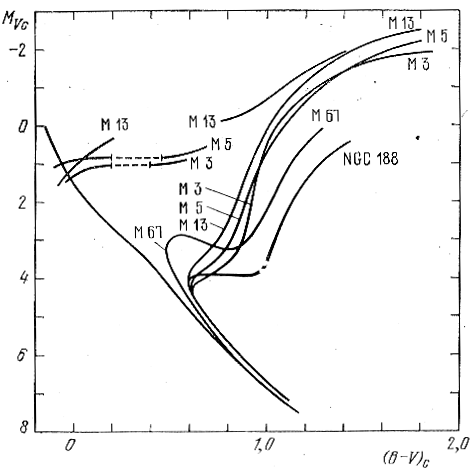
Рис. 86. Положение основных последовательностей старых скоплений М 3, М 5, М 13, М 67 и NGC 188 на диаграмме MVc, (В - V)c с учетом покровного эффекта и эволюционных эффектов (Сэндидж, 1962а).
Еще Фолкнер (1967) показал, что для объяснения наблюдаемой ширины главной последовательности необходимо принять, что у субкарликов в момент их образования Y ≈ 0,20. Таким образом, нужно считать, что начальная главная последовательность на диаграмме Mbol, lgTe обладает заметной шириной, очевидно, потому, что содержание гелия в звездах с малым содержанием металлов больше, чем допускали в свое врем Хазельгров и Хойл (1959). При этом вдоль верхней границы начальной главной последовательности располагаются звезды с высоким содержанием металлов, вдоль нижней - с низким. Учет покровного эффекта, как показывает рис. 85, не устраняет ширины начальной главной последовательности и на диаграмме MV, В - V.
Это обстоятельство значительно усложняет проблему точного определения расстояний до шаровых скоплений. Совершенно очевидно, что теперь мы вынуждены допустить существование целого семейства начальных главных последовательностей на диаграмме MV, В - V, зависящего от содержания гелия Y и содержания металлов Z. С этим семейством должно быть однозначно связано и семейство соответствующих кривых эволюционных отклонений.
К счастью, ширина главной последовательности ΔMV после учета покровного эффекта вряд ли превышает 0m,9 так что применение описанной выше методики все же позволит надеяться па определение модулей расстояния шаровыx скоплений с точностью до нескольких десятых звездной величины. В самом деле, если допустить, например, следуя Эггену и Сэндиджу (1962), что звезды главной последовательности скопления М 13 подобны "экстремальным" субкарликам, изображенным на рис. 85, а, - что правдоподобно, ибо средние значения δ(U - В) для звезд в М 13 и этих субкарликов равны +0m,23 и +0m,21 соответственно, - то можно непосредственно совместить главную последовательность М 13 с последовательностью "экстремальных" субкарликов, принимаемую в данном случае застандартную, не прибегая к процедуре покровного эффекта. Результаты такого совмещения показаны на рис. 87 (Эгген, Сэндидж, 1962). При этом модуль расстояния М 13 оказывается равным 14m,30. Ранее, пользуясь методом, основанным на учете покровного эффекта, Сэндидж (1962а, б) получил для М 13 значение m - M = 14m,43 (см. рис. 86).
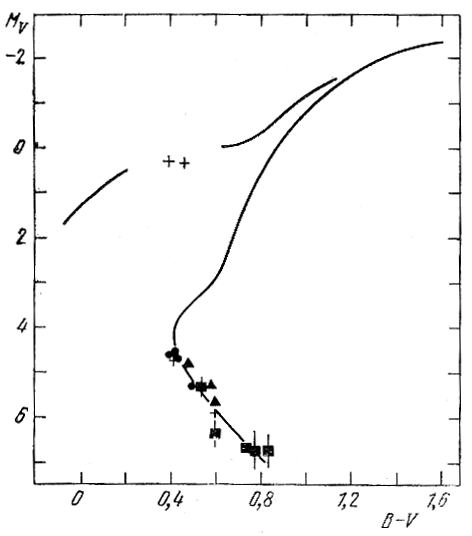
Рис. 87. Совмещение главной последовательности скопления М 13 на диаграмме MV, В - V со "стандартной" главной последовательностью "экстремальных" субкарликов с δ(U - В) ≥ 0m,16 (Эгген, Сэндидж, 1962).
В 1970 г, Сэндидж разработал новый метод определения расстояний до старых звездных скоплений, основанный на использовании зависимости между абсолютными величинами и ультрафиолетовыми избытками δ(U - В) карликов и субкарликов, впервые обнаруженной Эггеном и Сэндиджем (1962). Сэндидж разбил все звезды поля с известными πtr > 0",035 по величине присущего каждой из них значения δ(0,6) па четыре группы (A, B, C, D), принцип образования которых пояснен в табл. 6.2 (Сэндидж, 1970).
| Группа | <δ(0,6)> | <ΔMV> | n |
| A(-0m,05 ≤ δ(0,6) ≤ 0m,05) B(0m,06 ≤ δ(0,6) ≤ 0m,10) C(0m,11 ≤ δ(0,6) ≤ 0m,15) D(δ(0,6) ≥ 0m,16) |
0m,009 0m,076 0m,132 0m,218 |
-0m,06 ± 0m,03 0m,17 ± 0m,04 0m,56 ± 0m,08 1m,22 ± 0m,12 |
56 36 16 9 |
| B - V | MV |
| 0m,45 | 3m,78 |
| 0m,50 | 4m,10 |
| 0m,55 | 4m,45 |
| 0m,60 | 4m,78 |
| 0m,65 | 5m,02 |
| 0m,70 | 5m,32 |
| 0m,75 | 5m,60 |
| 0m,80 | 5m,85 |
| 0m,85 | 6m,10 |
| 0m,90 | 6m,34 |
| 0m,95 | 6m,58 |
Для каждой звезды по известным значениям V и πtr была вычислена абсолютная величина MV, а затем образованы разности ΔMV между MV и абсолютной величиной MV0, В - V точки на некоторой опорной последовательности с показателем цвета В - V, равным показателю цвета данной звезды. В качестве опорной Сэндидж принял главную последовательность звезд, входящих в состав старого населения диска Галактики. Форма этой последовательности, приведенной в табл. 6.3 для практически используемых значений В - V, совпадает со средней формой наблюдаемых главных последовательностей в скоплениях М 3, М 13, М 15 и М 92, освобождая нас от необходимости дополнительного учета эволюционных эффектов. Удивление может вызвать только то обстоятельство, что этот отрезок опорной последовательности совпадает с отрезком начальной главной последовательности Эггена (1965г).
Значения ΔMV коррелируют с δ(0,6). Средние значения <δ(0,6)> , <ΔMV> для групп А, В, С, D приведены в табл. 6.2. В столбце n указано число знеад в каждой группе. Зависимость между <ΔMV> и <δ(0,6)> представлена сплошной линией па рис. 88 (Cэндидж, 1970). О светлом кружке на этом рисунке мы скажем немного позже.
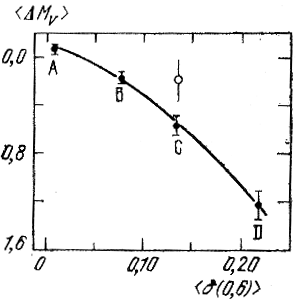
Рис. 88. Зависимость между значениями <ΔMV> и <δ(0,6)> для субкарликов с πtr > 0",035 (Сэндидж, 1970).
Определив для звезд главной последовательности рассматриваемого скопления после учета межзвездного поглощения света средние значения <(В - V)0> и <δ(U - В)>, можно найти по таблице Сэндиджа (1969б) значение <δ(0,6)> этих звезд, а с помощью рис. 88 - соответствующее ему значение <ΔMV> . Искомый модуль расстояния скопления определяется теперь выражением
|
|
(6.2) |
где V(<(В - V)0>) - видимая величина звезд главной последовательности скопления, соответствующая <(В - V)0> .
Для сравнения отметим, что найденный таким образом Сэндиджем (1970) модуль расстояния скопления М 13 оказался равным 14m,52, а средние абсолютные величины <MV> переменных типа RR Лиры в скоплениях М 3, М 15 и М 92 соответственно равными +0m,60, +0m,98 и +0m,91.
Этот метод не зависит от точности определения опорной последовательности (при выборе другой последовательности просто изменятся получаемые значения <ΔMV> . К сожалению, точность его всецело определяется небольшим числом субкарликов поля с δ(0,6) ≥ +0m,11 и πtr > 0",035, а также небольшой точностью определения их параллаксов.
Поскольку полученные описанным методом светимости переменных типа RR Лиры в скоплениях М 15 и М 92, относящихся к II типу Оостерхофа, оказались меньше светимости переменных в М 3 (скопления I типа Оостерхофа), вопреки вере и ожиданиям Сэндиджа (см. § 5.2), Сэндидж решил, что этот метод не может дать точные результаты и отдал предпочтение другому методу, на описании которого мы остановимся позже (см. § 6.9).
Само предположение о непрерывности изменения величины <ΔMV> с изменением δ(0,6) нуждается в проверке. Действительно, вскоре после появления рассмотренной работы Сэндиджа Эгген (1971г; 1973) привел серьезные доводы в пользу существования па диаграммах Mbol, lgTe и MI, R - I не полосы, а опять-таки последовательности субкарликов. Согласно Эггену (1973), для звезд группы С в табл. 6.2 следует принять значение <ΔMV> = +0m,2 ± 0m,1 при <δ(0,6)> = +0m,135 (чему соответствует светлый кружок на рис. 88). В таком случае мы уже не можем пользоваться кривой, изображенной на рис. 88, для определения значений <ΔMV> при δ(0,6), лежащих в интервале от 0m,05 до 0m,2. Может быть, кривая имеет разрыв, и при δ(0,6) ≥ +0m,16 все <ΔMV> = +1m,2.
К 1979 г. данные о величинах звезд главной последовательности в системе B, V были получены лишь для двенадцати шаровых скоплений: М 2 (Арп, 1959в), М 3 (Джонсон, Сэндидж, 1956; Сэндидж, 1970), М 5 (Арп, 1962б), М 13 (Сэндидж, 1970), М 15 (Сэндидж, 1970), М 71 (Арп, Хартвик, 1971), М 92 (Сэндидж, 1970), NGC 5053 (Уокер и др., 1976), NGC 6397 (Вулли и др., 1961), NGC 6752 (Карни, 1979), 47 Тuс (Хессер, Хартвик, 1977) и ω Сеn (Кэннон, Контизас, 1974). Далеко не для всех из них имеются наблюдения и в системе U.
Это обстоятельство наряду с отмеченными выше трудностями локализации главных последовательностей шаровых скоплений на диаграмме MV, В - V, до сих пор затрудняет точное решение проблемы определения расстояний до шаровых скоплений. Прежде чем продолжить описание паллиативных решений этой проблемы, необходимо рассмотреть основные физические характеристики шаровых скоплений и их членов.
<< 6.3 Общий вид диаграмм величина - показатель цвета звезд шаровых скоплений. Звезды главной последовательности в этих системах и субкарлики | Оглавление | 6.5 Спектры ярких звезд шаровых скоплений. Содержание тяжелых элементов в их атмосферах >>
|
Публикации с ключевыми словами:
звезды - Скопление
Публикации со словами: звезды - Скопление | |
См. также:
Все публикации на ту же тему >> | |