Гравитационная постоянная
ГРАВИТАЦИОННАЯ ПОСТОЯННАЯ - коэффициент пропорциональности G в ф-ле, описывающей закон всемирного тяготения Ньютона,
![]()
где F - сила, с к-рой точечные массы m1 и m2, находящиеся на расстоянии r друг от друга, взаимно притягиваются.
Численное значение и размерность Г. п. зависят от выбора единиц массы, длины и времени (табл. 1).
Табл. 1. - Значения гравитационной постоянной
| Наименование и обозначение | Единицы | Численное значение | ||
| длина | масса | время | ||
| Кавендишева Г.п. *, G | м | кг | с | (6,6745+0,0008).10-11м3/(кг.с2) |
| Геоцентрическая Г.п., |
м | масса Земли | с | (398 600,5+0,3).109м3/с2 |
| Гелиоцентрическая Г.п., |
м | масса Солнца | с | (132 712 438+5).1012м3/с2 |
| Селеноцентрическая Г.п., |
м | масса Луны | с | (4902,7+0,1).109м3/с2 |
| Гауссова Г.п., k | а.е. | масса Солнца | эфемеридные сутки | 0,01720209895 |
| Эйнштейнова Г.п., |
м | кг | - | (1,8664+0,0002).10-26м/кг |
| * Значение Г.п. приведено по определениям ГАИШ. | ||||
Г. п. G, имеющую размерность [L]3[M]-1[T]-2, где масса М, длина L и время Т выражены в единицах Международной системы единиц (СИ), иногда называют кавендишевой Г. п. в честь англ. учёного Г. Кавендиша, к-рый в 1798 г. впервые в лабораторном эксперименте с крутильными весами определил значение G. Все лабораторные эксперименты по определению G можно условно разделить на две группы.
В первой группе экспериментов сила гравитац. взаимодействия сравнивается с упругой силой нити горизонтальных крутильных весов. Они представляют собой лёгкое коромысло, на концах к-рого укреплены пробные массы. За середину коромысло подвешено на тонкой упругой нити. Величина гравитац. взаимодействия определяется по углу закручивания нити (статич. метод), вызванному притяжением пробных масс к расположенным вблизи эталонным массам.
Во второй группе сила гравитац. взаимодействия между пробными и эталонными массами сравнивается с силой тяжести, для чего используются рычажные весы. Этим способом Г. п. была впервые определена нем. физиком Ф. Йолли в 1878 г. Впоследствии опыты Кавендиша и Йолли неоднократно повторялись, однако в наше время они представляют лишь исторический интерес.
Значение Г. п., включённое Международным астрономическим союзом (MAC) в Систему астрономических постоянных (САП) 1976 г., к-рым продолжают пользоваться, получено с помощью крутильных весов в 1942 г. П. Хейлом и П. Хржановским (США).
В СССР Г. п. впервые была определена в Государственном астрономическом институте имени П. К. Штернберга (ГАИШ) в 1975-78 гг. Как и в экспериментах Хейла и Хржановского, был применён динамич. метод, сущность к-рого состоит в следующем. Частота крутильных колебаний w горизонтальных весов в гравитац. поле эталонных масс определяется выражением:
![]()
Частота w измеряется в процессе эксперимента, величины m и J могут быть вычислены. Коэфф. m зависит от размеров и плотностей эталонных масс и крутильных весов, а также от их взаимного расположения. Момент инерции крутильных весов J определяется их геометрич. размерами и массой. Остаются два неизвестных параметра - крутильная жесткость t и Г. п. Поэтому для исключения t и определения G нужно иметь два таких ур-ния (т. е. провести измерения w по крайней мере для двух различных положений эталонных масс). Т. о., для определения Г. п. динамич. методом необходимо произвести измерения: 1) геометрич. размеров и плотностей эталонных масс и крутильных весов; 2) положения эталонных масс относительно крутильных весов; 3) частот крутильных колебаний при различных положениях эталонных масс.
 |
|
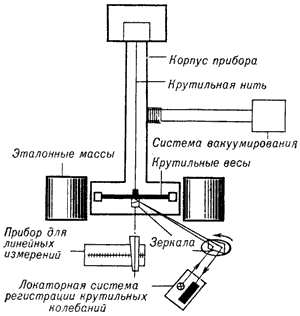
Схема экспериментальной установки |
На рис. приведена схема экспериментальной установки ГАИШ. Т. к. параметры, приведённые в пункте 1), не меняются от эксперимента к эксперименту, то их измерение достаточно провести один раз для всех экспериментов. Измерения остальных параметров должны производиться в каждом эксперименте. Т. о., для получения одного значения Г. п. при разных положениях эталонных масс (перестановка эталонных масс в процессе эксперимента производится автоматически) определяются расстояния между эталонными и пробными массами (с помощью прибора для линейных измерений), а фотоэлектрич. система регистрации измеряет частоту крутильных колебаний. Такие эксперименты повторяются многократно, поэтому для уменьшения случайных погрешностей вычисляют ср. значение Г. п. и его среднеквадратическую погрешность.
Во всех совр. определениях Г. п. (кавендишевой) были использованы крутильные весы. Помимо собственно динамич. метода применялись также его модификации - резонансный и ротационный методы. В резонансном методе эталонные массы вращаются вокруг оси крутильной нити с частотой, равной частоте собственных колебаний весов, что приводит к резонансному возбуждению крутильных колебаний. По изменению амплитуды колебаний можно судить о величине Г. п. В ротационном методе платформа, на к-рой установлены крутильные весы и эталонные массы, вращается вокруг вертикальной оси. Г. п. определяется по измерениям ускорения платформы, а также постоянного угла поворота крутильных весов относительно эталонных масс.
Результаты совр. определений Г. п. приведены в табл. 2. Среднеквадратические погрешности измерений указывают на внутр. сходимость каждого результата. Лучшие из них (три последних результата) не перекрываются между собой в доверительных интервалах. Это связано с тем, что определение кавендишевой Г. п. требует проведения абс. измерений, и поэтому в отдельных результатах возможны систематич. погрешности. Очевидно, значение Г. п. может быть достоверным только при учёте различных определений Г. п., полученных разными методами.
Табл.2. - Результаты современных определений кавендишевой гравитационной постоянной.
| Авторы, место проведения измерений, год публикации | Метод | Значение Г.п., 10-11 м3/(кг.с2) |
| Хейл, Хржановский (США), 1942 | Динамический | 3,373+0,005 |
| Роуз, Паркер, Бимс и др. (США), 1969 | Ротационный | 6,674+0,004 |
| Реннер (Венгрия), 1970 | Динамический | 6,670+0,008 |
| Фаси, Понтикис, Лукас(Франция), 1972 | Резонансный | 6,6714+0,0006 |
| Сагитов, Милюков, Монахов и др. (1978) | Динамический | 6,6745+0,0008 |
| Лютер, Тоулер (США), 1982 | Динамический | 6,6726+0,0005 |
Г. п., выраженные в астрономич. единицах, определяются на основании астрономич. наблюдений и 3-го закона Кеплера, к-рый явл. следствием закона тяготения (1).
Геоцентрическая Г. п. ![]() (равная
произведению кавендишевой Г. п. на массу Земли
(равная
произведению кавендишевой Г. п. на массу Земли
![]() ) используется
при расчётах движения в поле тяготения
Земли небесных тел, как естественных, так и
искусственных. Наиболее точно геоцентрич. Г.
п. определяется по наблюдениям ИСЗ или КА,
направляемых к др. планетам, т. к. на их
движение меньше влияет неоднородность
плотности Земли и неправильность её фигуры.
) используется
при расчётах движения в поле тяготения
Земли небесных тел, как естественных, так и
искусственных. Наиболее точно геоцентрич. Г.
п. определяется по наблюдениям ИСЗ или КА,
направляемых к др. планетам, т. к. на их
движение меньше влияет неоднородность
плотности Земли и неправильность её фигуры.
Аналогично гелиоцентрическая, селеноцентрическая и др. планетоцентрические Г. п. предназначены для расчёта движения в гравитац. полях соответственно Солнца, Луны и планет. В астрономии применяется и иной подход к определению Г. п. Ей априорно приписывается нек-рое фиксированное значение; две из трёх физ. величин (масса и время), задающих размерность Г. п., определяются из наблюдений, тогда ед. длины становится производной величиной. Так вводится гауссова Г. п. k. По мере уточнения массы Солнца (ед. массы) и эфемеридных суток (ед. времени) изменяется величина а. е.
Эйнштейнова Г. п. ![]() используется в
теоретич. физике. Она связана с
кавендишевой Г. п. соотношением:
используется в
теоретич. физике. Она связана с
кавендишевой Г. п. соотношением: ![]() .
.
Как в теории тяготения Ньютона, так и в общей теории относительности (ОТО) А. Эйнштейна Г. п. рассматривается как универсальная константа природы, не изменяющаяся в пространстве и времени и не зависящая от физ. и хим. св-в среды и гравитирующих масс. Существуют варианты теории гравитации, имеющие в слабых полях одинаковый ньютоновский предел, но дающие ряд предсказаний, отличных от предсказаний ОТО, в т. ч. переменность Г. п. Напр., теория П. Дирака, созданная ещё в 1930-е гг., предсказывает изменение Г. п. (DG) со временем на величину ~DG/G » 6.10-11 в год. Нек-рые варианты теории гравитации предполагают зависимость Г. п. от расстояния между притягивающимися телами. Однако имеющиеся наблюдательные данные, а также специально поставленные лабораторные эксперименты пока не позволяют обнаружить это гипотетич. изменение Г. п.
Лит.: Сагитов М. У., Постоянная тяготения и масса Земли, М., 1969; Новое определение кавендишевой гравитационной постоянной, "ДАН СССР", 1979, т. 245, № 3, с. 567-69; Абалакин В. К., Основы афемеридной астрономии, М., 1979.
(В.К. Милюков, М.У. Сагитов)
В.К. Милюков, М. У. Сагитов, "Физика Космоса", 1986
Глоссарий Astronet.ru
|
Публикации с ключевыми словами:
гравитационная постоянная
Публикации со словами: гравитационная постоянная |

|
|
См. также:
| |