Гравитационный коллапс
ГРАВИТАЦИОННЫЙ КОЛЛАПС
Содержание:
1. Введение
2. Условия гидростатического
равновесия звезды н возникновение
гравитационного коллапса
3. Динамика гравитационного
коллапса звёзд с различными массами
железного ядра (![]() ).
).
4. Термоядерный взрыв углеродно-кислородных
звёзд (![]() ) и развитие
гравитационного коллапса
) и развитие
гравитационного коллапса
5. Вспышки сверхновых звёзд,
статистика коллапсирующих звёзд,
возможности наблюдений
Г. к. звезды - катастрофически быстрое её
сжатие под действием собств. сил тяготения -
может произойти после прекращения в центр.
области звезды термоядерных реакций. С
истощением в звезде запасов ядерной
энергии и угасанием центрального источника
энергии непосредственно нарушается её
тепловое, а затем и гидростатическое (механич.)
равновесие. При этом ослабляются силы,
противодействующие тяготению, и возникают
условия для быстрого сжатия звезды. Г. к.
рассматривают как один из возможных путей
завершения эволюции
звёзд (с ![]() ),
приводящей к образованию нейтронных звёзд
или даже (в случае релятивистского Г. к.)
чёрных дыр. Выброс внеш. слоев звезды,
возможный при Г. к. её центр. области,
приводит к появлению сверхновой звезды.
),
приводящей к образованию нейтронных звёзд
или даже (в случае релятивистского Г. к.)
чёрных дыр. Выброс внеш. слоев звезды,
возможный при Г. к. её центр. области,
приводит к появлению сверхновой звезды.
Термоядерные реакции служат источником
энергии звезды и обеспечивают в ней
гидростатич. и тепловое равновесие вплоть
до образования в её центр. области атомных
ядер группы железа. .Эти ядра имеют
наибольшую энергию
связи на нуклон, так что
синтез ядер более тяжёлых, чем ядра железа,
уже не сопровождается выделением энергии, а,
наоборот, требует затрат энергии. Лишённая
с этого момента термоядерных источников
энергии, звезда не может скомпенсировать
потери энергии во внешнее пространство, тем
более что к концу "термоядерного"
этапа эволюции эти потери чрезвычайно
возрастают. К обычным потерям энергии с
поверхности звезды (испусканию фотонов
фотосферой звезды) здесь прибавляются
объёмные потери энергии, обусловленные
интенсивным излучением нейтрино
(v) и антинейтрино (![]() ) центр. областью звезды.
Объёмные потери энергии, как показывают
расчёты эволюции звёзд, становятся
преобладающими над потерями с поверхности
при темп-pax в центре звезды
) центр. областью звезды.
Объёмные потери энергии, как показывают
расчёты эволюции звёзд, становятся
преобладающими над потерями с поверхности
при темп-pax в центре звезды ![]() . Для
поздней стадии ядерной эволюции достаточно
массивной звезды это условие выполняется с
избытком - при синтезе ядер группы железа
темп-pa в центре звезды с
. Для
поздней стадии ядерной эволюции достаточно
массивной звезды это условие выполняется с
избытком - при синтезе ядер группы железа
темп-pa в центре звезды с ![]() достигает 3.109К. У маломассивных звёзд, с
массой около нижнего предела
достигает 3.109К. У маломассивных звёзд, с
массой около нижнего предела ![]() , темп-pa
в центре в конце ядерной эволюции тоже
достигает значения
, темп-pa
в центре в конце ядерной эволюции тоже
достигает значения ![]() и объёмные
потери энергии в виде нейтринного
излучения становятся основными.
и объёмные
потери энергии в виде нейтринного
излучения становятся основными.
Нескомпенсированные потери энергии нарушают равновесие звезды. Создаются условия для сжатия её центр. области под действием собств. сил тяготения. Звезда расходует теперь гравитационную энергию, выделяющуюся при сжатии. Темп-pa в сжимающейся звезде возрастает (см. Вириала теорема). Сначала сжатие звезды идёт медленно, так что условие гидростатич. равновесия ещё выполняется. Наконец, темп-ра достигает таких высоких значений, »(5-10).109К, что ядра группы железа теряют устойчивость. Они распадаются на ядра гелия, нейтроны и протоны (на первом этапе распада 5626Fe ® 1342He + 4n - 124,4 МэВ, а при дальнейшем росте темп-ры распадаются и ядра Не: 42Не ® 2n + 2р - 26,21МэВ). Распад ядер требует значит. затрат энергии, т. к. представляет собой как бы всю цепь термоядерных реакций синтеза от водорода до железа, но идущую в обратном направлении (не с выделением, а с поглощением энергии). Темп-pa в недрах звезды всё же растёт (за счёт гравитац. сжатия), но из-за распада ядер железа, требующего затрат энергии, не так быстро, как это было бы необходимо для приостановления сжатия. В результате потерь энергии на нейтринное излучение и распада ядер происходит своеобразный взрыв звезды - взрыв внутрь (иногда в научной литературе его наз. имплозией, в отличие от эксплозии - взрыва наружу, вызванного быстрым высвобождением энергии). При имплозии вещество центр. области звезды падает к центру со скоростью, близкой к скорости свободного падения. Возникающая при этом гидродинамическая волна разрежения втягивает последовательно в режим падения всё более удалённые от центра слои звезды. Начавшийся Г. к. при определённых условиях может затормозиться или даже остановиться, но в ряде случаев может безостановочно продолжаться, переходя в т. н. релятивистский гравитационный коллапс.
Выяснение всего комплекса условий, приводящих к Г. к.,- задача крайне сложная. Один из важных этапов решения этой задачи - исследование условий гидростатич. равновесия на поздних стадиях эволюции звезды с привлечением ур-ния состояния вещества в звезде.
2. Условия гидростатического равновесия звезды и возникновение гравитационного коллапса
На всём протяжении эволюц. развития
звезды, связанного с термоядерными
реакциями в её центр. области, в звезде за
редким исключением поддерживается
гидростатич. равновесие. Оно заключается в
равенстве (в каждой точке звезды и в любой
момент времени) сил тяготения ![]() и
сил отталкивания частиц вещества,
обусловленных давлением р, F-= -Dр/Dr [здесь
фигурируют абс. величины этих сил, r -
расстояние от центра до рассматриваемой
точки звезды,
и
сил отталкивания частиц вещества,
обусловленных давлением р, F-= -Dр/Dr [здесь
фигурируют абс. величины этих сил, r -
расстояние от центра до рассматриваемой
точки звезды, ![]() - масса внутри сферы
радиуса r, р - плотность вещества, -Dр/Dr -
приближённое выражение радиальной
составляющей градиента давления в
окрестности рассматриваемой точки].
Усреднённое для всей звезды в целом ур-ние
гидростатич. равновесия можно приближённо
записать в виде:
- масса внутри сферы
радиуса r, р - плотность вещества, -Dр/Dr -
приближённое выражение радиальной
составляющей градиента давления в
окрестности рассматриваемой точки].
Усреднённое для всей звезды в целом ур-ние
гидростатич. равновесия можно приближённо
записать в виде:
![]()
где ![]() и R - полная масса и радиус звезды,
rс
и рс - плотность и давление в центре звезды.
Это ур-ние позволяет, в частности, оценить
темп-ру Тс около центра звезды. Если принять,
что вещество там подчиняется ур-нию
состояния идеального газа, то
и R - полная масса и радиус звезды,
rс
и рс - плотность и давление в центре звезды.
Это ур-ние позволяет, в частности, оценить
темп-ру Тс около центра звезды. Если принять,
что вещество там подчиняется ур-нию
состояния идеального газа, то
![]() , где m
- молекулярная масса вещества звезды, R0
- универсальная газовая постоянная. Для
звёзд типа Солнца Тс~107К, для
коллапсирующих (более массивных) звёзд она
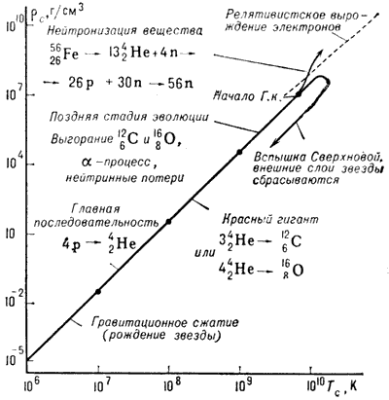
гораздо выше. На рис. 1 показана возможная
схема эволюц. пути массивной звезды (
, где m
- молекулярная масса вещества звезды, R0
- универсальная газовая постоянная. Для
звёзд типа Солнца Тс~107К, для
коллапсирующих (более массивных) звёзд она
гораздо выше. На рис. 1 показана возможная
схема эволюц. пути массивной звезды (![]() ) от момента её рождения из газово-пылевого
облака до момента полного истощения в её
центр. области термоядерного топлива и
наступления Г. к. (точка разветвления).
) от момента её рождения из газово-пылевого
облака до момента полного истощения в её
центр. области термоядерного топлива и
наступления Г. к. (точка разветвления).
 |
|
Рис. 1. Эволюционный путь звезды с |
Эволюция звезды после "выключения" термоядерных источников энергии, строго говоря, может идти двумя путями: при сохранении гидростатич. равновесия и гидродинамич. путём, когда силы тяготения станут существенно преобладающими (F+>F-). Путь, по к-рому пойдёт эволюция звезды, зависит от того, как давление вещества звезды изменяется с изменением темп-ры и плотности, т. е. от ур-ния состояния вещества. Если увеличение плотности при сжатии вещества силами тяготения не сопровождается достаточно интенсивным ростом давления, то в звезде создаются предпосылки для нарушения гидростатич. равновесия и развития Г. к. Связь давления с плотностью в случае быстрого сжатия вещества (имеющего характер адиабатического процесса) имеет вид: рс ~ rgc (g называется показателем адиабаты).
В свою очередь, плотность вещества определяется размерами звезды rc ~ 1/R3. Выражение для сил отталкивания может быть записано, следовательно, в виде:
![]()
Зависимость сил тяготения от радиуса звезды даётся соотношением:
![]()
Из соотношений (2) и (3) видно, что силы тяготения быстрее нарастают с уменьшением радиуса звезды по сравнению с силами давления, если
5 > 1 + 3g или g < 4/3 (4),
При g < 4/3 любое случайное малое гидродинамич. возмущение типа сжатия будет нарастать. Упругость вещества в этом случае недостаточна для предотвращения Г. к. В противном случае (при g > 4/3) гидростатич. равновесие устойчиво: случайно возникшие уплотнения будут рассасываться и затухать. В строгой теории гидростатич. устойчивости звёзд учитывают неодинаковость g для различных слоев звезды. Фактически условия Г. к. наступают, когда в центр. области g < 4/3, а во внеш. слоях ещё выполняется условие g > 4/3. На рис. 2 приведены результаты теоретич. расчётов величины g в зависимости от плотности и темп-ры вещества. Проведённые линии уровня g = 4/3 отчётливо выделяют "овраг неустойчивости" (область с g < 4/3). Когда в процессе эволюции в "овраг неустойчивости" попадает значит. часть центр. области звезды, начинается её Г. к.
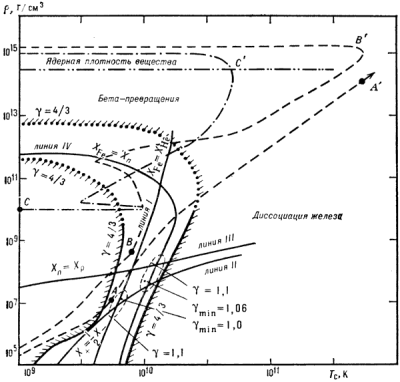 |
Рис. 2. Диаграмма взаимных превращений
различных частиц звёздного вещества и его
упругих свойств в зависимости от плотности
(r) и темп-ры (Тс). Области наименьшей
упругости вещества (с показателем адиабаты gмин = 1 ,0
и 1,06) лежат вблизи пересечения линий равных
весовых концентраций X: I - ядер железа и
гелия (слева от линии преобладают ядра
железа, справа - гелия, на самой линии XFe=XHe); II - электрон-позитронных пар и
атомных электронов (выше этой линии
преобладают электроны); III - нейтронов и
протонов (выше линии преобладают нейтроны);
IV - ядер железа и нейтронов (выше и правее
линии преобладают нейтроны). На диаграмме
изображены пути центральных точек звёзд: с
массой |
3. Динамика гравитационного коллапса
звёзд с различными массами железного ядра
(![]() )
)
Выявление физ. процессов, приводящих к значениям показателя g < 4/3 представляет собой одну из важных проблем теории Г. к. При высоких темп-pax и давлениях, характерных для стадии полного прекращения термоядерных реакций в звезде, плотность вещества в центре звезды превышает в миллионы или даже в миллиарды раз плотность твёрдых тел на поверхности Земли. Несмотря на это, звёздное вещество по св-вам близко к идеальному газу, т. к. кинетич. энергия образующих его частиц значительно превышает потенц. энергию их взаимодействия. От обычного идеального газа вещество центр. области звезды отличается тем, что образующие его разнородные частицы (фотоны, электроны, позитроны, протоны, нейтроны и разнообразные сложные атомные ядра) при взаимодействии могут испытывать различные превращения. При столкновении электрона с позитроном происходит их аннигиляция, и рождаются фотоны. В свою очередь, фотоны высоких энергий при столкновении с др. частицами могут рождать пары электрон - позитрон или путём фотоядерных реакций вызывать диссоциацию сложных ядер. Протоны и нейтроны участвуют в разнообразных ядерных реакциях со сложными ядрами, к-рые также могут взаимодействовать между собой. Нуклоны и ядра испытывают ещё различные бета-превращения (см. Бета-процессы). Подобные взаимные превращения частиц при определённой достаточно высокой темп-ре достигают динамич. равновесия (ядерного статистич. равновесия), и это состояние определяет равновесные концентрации всех частиц и все св-ва звёздного вещества, в т. ч. границы и глубину "оврага неустойчивости".
Наряду с превращениями частиц, к-рые
протекают с равной вероятностью в прямом и
обратном направлениях (так что они
уравновешивают друг друга), в конце
термоядерной стадии эволюции звёзд значит.
интенсивности достигают бета-превращения.
В бета-превращениях обязательно участвуют
нейтрино и антинейтрино, к-рые сразу же
после своего рождения покидают звезду (для
них толща звезды прозрачна). Поэтому бета-превращения
имеют односторонний характер - реакций
взаимодействия нейтрино и антинейтрино с к.-л.
другими частицами (напр., захват нейтрино
протоном) в звезде не происходит.
Односторонний характер бета-превращений
означает, что в звёздном веществе нет
полного термодинамического равновесия.
Количественно вклад бета-превращений
особенно существен в левой верхней части
"оврага неустойчивости", куда могут
попасть менее массивные звёзды, с ![]() .
Из-за отсутствия термодинамич. равновесия
изображённые в этой части рис. 2 линии носят
условный характер (они были фактически
вычислены с использованием весьма грубого
приближения). Строгое определение физ.
условий при существенном вкладе бета-превращений
требует последовательного расчёта их
кинетики, самосогласованного с расчётом
эволюции и Г. к. звезды. Тем не менее могло бы
устанавливаться т. н. кинетич. равновесие, в к-ром уравновешивались бы все бета-превращения,
за исключением тех, к-рые могли бы быть
вызваны свободно улетающими нейтрино и
антинейтрино. При таком равновесии для
быстрых гидродинамических возмущений, за
которыми не поспевают бета-превращения, "овраг
неустойчивости" мелеет и сужается. А это
означает, что могут развиваться только
неустойчивости с характерным временем бета-превращений.
Поэтому у маломассивных звёзд Г. к. должен
развиваться сравнительно медленно. В общем
случае задачу развития Г. к. следует решать
с учётом кинетики всех бета-превращений.
.
Из-за отсутствия термодинамич. равновесия
изображённые в этой части рис. 2 линии носят
условный характер (они были фактически
вычислены с использованием весьма грубого
приближения). Строгое определение физ.
условий при существенном вкладе бета-превращений
требует последовательного расчёта их
кинетики, самосогласованного с расчётом
эволюции и Г. к. звезды. Тем не менее могло бы
устанавливаться т. н. кинетич. равновесие, в к-ром уравновешивались бы все бета-превращения,
за исключением тех, к-рые могли бы быть
вызваны свободно улетающими нейтрино и
антинейтрино. При таком равновесии для
быстрых гидродинамических возмущений, за
которыми не поспевают бета-превращения, "овраг
неустойчивости" мелеет и сужается. А это
означает, что могут развиваться только
неустойчивости с характерным временем бета-превращений.
Поэтому у маломассивных звёзд Г. к. должен
развиваться сравнительно медленно. В общем
случае задачу развития Г. к. следует решать
с учётом кинетики всех бета-превращений.
В любом случае вещество звезды, попадая в
"овраг неустойчивости", теряет
упругость, и звезда, в конечном счёте, не
может противодействовать силам тяготения,
что ведёт к развитию Г. к. Строгие расчёты
для звезды с массой ![]() (масса железного
ядра
(масса железного
ядра ![]() , остальное - кислородная
внеш. оболочка) показывают остановку Г. к.
при достижении в центре звезды плотности rс
~ 1013 г/см3 и темп-ры Тс ~ 1011К. После остановки Г.
к. начинается процесс образования горячей
нейтронной звезды. При этом продолжается
довольно медленное увеличение (вся быстрая
стадия Г. к. до остановки характеризуется
гидродинамич. временем ~0,1 с) центр.
плотности до rс~1015 г/см3 и темп-ры
Тс ~ 1012К (за
время »3с). Затем происходит ещё более
медленный процесс охлаждения горячей
нейтронной звезды, завершающийся
образованием холодной нейтронной звезды,
для к-рой масса
, остальное - кислородная
внеш. оболочка) показывают остановку Г. к.
при достижении в центре звезды плотности rс
~ 1013 г/см3 и темп-ры Тс ~ 1011К. После остановки Г.
к. начинается процесс образования горячей
нейтронной звезды. При этом продолжается
довольно медленное увеличение (вся быстрая
стадия Г. к. до остановки характеризуется
гидродинамич. временем ~0,1 с) центр.
плотности до rс~1015 г/см3 и темп-ры
Тс ~ 1012К (за
время »3с). Затем происходит ещё более
медленный процесс охлаждения горячей
нейтронной звезды, завершающийся
образованием холодной нейтронной звезды,
для к-рой масса ![]() ещё допустима (см.
Нейтронные
звёзды).
ещё допустима (см.
Нейтронные
звёзды).
Такой же расчёт (в рамках той же физ.
модели) Г. к. массивной звезды, с ![]() (из
них масса железного ядра
(из
них масса железного ядра ![]() , остальное
- кислородная внеш. оболочка), приводит к
иному результату. Остановки Г. к. не
получается, и быстрая гидродинамич. стадия
Г. к. продолжается релятивистским Г. к., т. е.
звезда превращается в чёрную дыру. На рис. 2
нанесены траектории центр. точки звезды для
обоих обсуждаемых расчётов Г. к.:
, остальное
- кислородная внеш. оболочка), приводит к
иному результату. Остановки Г. к. не
получается, и быстрая гидродинамич. стадия
Г. к. продолжается релятивистским Г. к., т. е.
звезда превращается в чёрную дыру. На рис. 2
нанесены траектории центр. точки звезды для
обоих обсуждаемых расчётов Г. к.: ![]() (BB`) и
(BB`) и ![]() (АА`). Видно, что остановка Г. к. в случае
BB` происходит после пересечения траектории
центра звезды с правой (внешней) границей
"оврага неустойчивости", где
показатель адиабаты g = 4/3.
В точке остановки
показатель g >> 4/3. В случае АА` траектория
проходит (рис. 2) правее траектории ВВ`, и,
несмотря на то что g > 4/3
после пересечения
"оврага неустойчивости", Г. к. даже не
тормозится. Т. о., при наличии мощного
нейтринного излучения увеличение
упругости звёздного вещества ещё
недостаточно для остановки Г. к.
(АА`). Видно, что остановка Г. к. в случае
BB` происходит после пересечения траектории
центра звезды с правой (внешней) границей
"оврага неустойчивости", где
показатель адиабаты g = 4/3.
В точке остановки
показатель g >> 4/3. В случае АА` траектория
проходит (рис. 2) правее траектории ВВ`, и,
несмотря на то что g > 4/3
после пересечения
"оврага неустойчивости", Г. к. даже не
тормозится. Т. о., при наличии мощного
нейтринного излучения увеличение
упругости звёздного вещества ещё
недостаточно для остановки Г. к.
К физ. причинам, вызывающим остановку Г. к.
в случае ![]() , следует отнести прежде всего
прекращение всех процессов взаимного
превращения частиц, идущих с затратой
энергии, и образование большого числа
нуклонов из ядер группы железа и ядер гелия.
Образовавшийся нуклонный газ (с избытком
частично вырожденных нейтронов)
значительно повышает упругость вещества,
при темн-ре недр Тс > 1010 К (значение
g для
такого газа приближается к 5/3). Не менее
важным фактором следует считать
возникающую на определённом этапе сжатия
непрозрачность толщи звезды для
нейтринного излучения. Нейтрино и
антинейтрино, беспрепятственно уходившие
до этого из звезды, в новых условиях будут
поглощаться веществом звезды. В результате
суммарные потери энергии у звезды
уменьшатся, к тому же одновременно
возникающий перенос энергии нейтринным
излучением из центра звезды в её внеш. слои
может непосредственно затруднить Г. к. внеш.
слоев звезды. Можно считать, что
возникновение нейтринной непрозрачности
на такой стадии Г. к., когда восстановилась
достаточная упругость вещества (g > 4/3),
способствует остановке Г. к. Теория
нейтринных потерь энергии, включая вопросы
непрозрачности и переноса энергии
нейтринным излучением, явл. одной из
главных задач в исследовании Г. к. В
принципе остановке Г. к. могут
содействовать также вращение и магн. поле
звезды, но количественно эти важные эффекты
пока учесть довольно трудно.
, следует отнести прежде всего
прекращение всех процессов взаимного
превращения частиц, идущих с затратой
энергии, и образование большого числа
нуклонов из ядер группы железа и ядер гелия.
Образовавшийся нуклонный газ (с избытком
частично вырожденных нейтронов)
значительно повышает упругость вещества,
при темн-ре недр Тс > 1010 К (значение
g для
такого газа приближается к 5/3). Не менее
важным фактором следует считать
возникающую на определённом этапе сжатия
непрозрачность толщи звезды для
нейтринного излучения. Нейтрино и
антинейтрино, беспрепятственно уходившие
до этого из звезды, в новых условиях будут
поглощаться веществом звезды. В результате
суммарные потери энергии у звезды
уменьшатся, к тому же одновременно
возникающий перенос энергии нейтринным
излучением из центра звезды в её внеш. слои
может непосредственно затруднить Г. к. внеш.
слоев звезды. Можно считать, что
возникновение нейтринной непрозрачности
на такой стадии Г. к., когда восстановилась
достаточная упругость вещества (g > 4/3),
способствует остановке Г. к. Теория
нейтринных потерь энергии, включая вопросы
непрозрачности и переноса энергии
нейтринным излучением, явл. одной из
главных задач в исследовании Г. к. В
принципе остановке Г. к. могут
содействовать также вращение и магн. поле
звезды, но количественно эти важные эффекты
пока учесть довольно трудно.
К моменту остановки Г. к. у звезды
образуется резко выраженная гетерогенная
структура: сильно сжатое ядро с массой ![]() и
сравнительно мало сжавшаяся с начала Г. к.
оболочка, содержащая остальную массу
звезды. Как показывают расчёты, после
остановки Г. к. центральной области звезды
внеш. слои продолжают падать к центру и,
натолкнувшись на плотное ядро, быстро
тормозятся. Торможение падающего, или аккрецирующего (см.
Аккреция),
вещества осуществляется в области ударного
скачка на границе ядра и падающей оболочки.
При достаточно резкой остановке сжатия
ядра этот скачок может преобразоваться в
мощную ударную волну, распространяющуюся
от границы ядра к периферии звезды. На рис. 3,
построенном на основе одного из расчётов Г. к. с очень резкой остановкой
для звезды с
и
сравнительно мало сжавшаяся с начала Г. к.
оболочка, содержащая остальную массу
звезды. Как показывают расчёты, после
остановки Г. к. центральной области звезды
внеш. слои продолжают падать к центру и,
натолкнувшись на плотное ядро, быстро
тормозятся. Торможение падающего, или аккрецирующего (см.
Аккреция),
вещества осуществляется в области ударного
скачка на границе ядра и падающей оболочки.
При достаточно резкой остановке сжатия
ядра этот скачок может преобразоваться в
мощную ударную волну, распространяющуюся
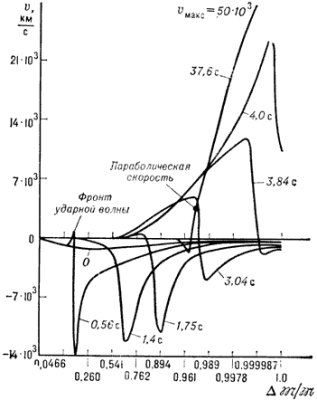
от границы ядра к периферии звезды. На рис. 3,
построенном на основе одного из расчётов Г. к. с очень резкой остановкой
для звезды с
![]() показано, как по мере
распространения ударной волны движение
вещества к центру тормозится и сменяется
разлётом наружу. Первоначально (рис. 3)
ударная волна сформировалась как ударный
скачок при
показано, как по мере
распространения ударной волны движение
вещества к центру тормозится и сменяется
разлётом наружу. Первоначально (рис. 3)
ударная волна сформировалась как ударный
скачок при ![]() в момент 0,56с. Она
продолжает существовать до момента 1,75с в
виде ударного скачка, пока вещество за её
фронтом полностью тормозится. В дальнейшем
происходит распространение ударной волны. Её скорость возрастает с приближением
фронта волны к поверхности звезды, т. к. она
движется из плотных ко всё более
разреженным слоям вещества. Ударная волна
ускоряется также за счёт детонации
ядерного горючего во внеш. слоях звезды. Осн.
процессом такого рода, учитываемым в
расчёте, явл. превращение ядер 2168O
® 3216S
+ 16,54
МэВ. В конце концов ударная волна может
вызвать отрыв части оболочки от звезды.
Примерно так могла бы происходить вспышка
сверхновой звезды.
в момент 0,56с. Она
продолжает существовать до момента 1,75с в
виде ударного скачка, пока вещество за её
фронтом полностью тормозится. В дальнейшем
происходит распространение ударной волны. Её скорость возрастает с приближением
фронта волны к поверхности звезды, т. к. она
движется из плотных ко всё более
разреженным слоям вещества. Ударная волна
ускоряется также за счёт детонации
ядерного горючего во внеш. слоях звезды. Осн.
процессом такого рода, учитываемым в
расчёте, явл. превращение ядер 2168O
® 3216S
+ 16,54
МэВ. В конце концов ударная волна может
вызвать отрыв части оболочки от звезды.
Примерно так могла бы происходить вспышка
сверхновой звезды.
 |
|
Рис. 3. Распределение скоростей и движения
слоев звезды с мaccoй |
Но в более последовательных расчётах Г. к.
с остановкой достаточно мощной ударной
волны со сколько-нибудь значительной
кинетич. энергией разлёта оторвавшихся
слоев не получается. В расчёте Г. к. для
звезды с массой ![]() (случай ВВ` на рис. 2)
вообще не получилось никакого выброса внеш.
слоев, даже с учётом эффекта вращения.
Наблюдения же, напротив, свидетельствуют о
тесной связи нейтронных звёзд-пульсаров и
вспышек сверхновых. С этой точки зрения
особый интерес представляют исследования Г.
к. для звёзд малых масс, приближающихся к т.
н. Чандрасекара пределу (
(случай ВВ` на рис. 2)
вообще не получилось никакого выброса внеш.
слоев, даже с учётом эффекта вращения.
Наблюдения же, напротив, свидетельствуют о
тесной связи нейтронных звёзд-пульсаров и
вспышек сверхновых. С этой точки зрения
особый интерес представляют исследования Г.
к. для звёзд малых масс, приближающихся к т.
н. Чандрасекара пределу (![]() для железной
звезды и
для железной
звезды и ![]() для углеродной). Дело в том,
что в этих исследованиях был обнаружен
весьма эффективный механизм выброса
оболочки звезды (см. раздел 4). На рис. 2
нанесена траектория СС`, изображающая Г. к.
для центра звезды с массой
для углеродной). Дело в том,
что в этих исследованиях был обнаружен
весьма эффективный механизм выброса
оболочки звезды (см. раздел 4). На рис. 2
нанесена траектория СС`, изображающая Г. к.
для центра звезды с массой ![]() к-рый
сопровождается выбросом внеш. слоев (качеств.
сторону этого эффекта поясняет рис. 3).
к-рый
сопровождается выбросом внеш. слоев (качеств.
сторону этого эффекта поясняет рис. 3).
4. Термоядерный взрыв углеродно-кислородных
звёзд (![]() ) и развитие
гравитационного коллапса
) и развитие
гравитационного коллапса
Выше уже говорилось, что главным
механизмом, приводящим к потере гидростатич.
устойчивости маломассивных звёзд, явл. бета-превращения,
а точнее - захват электронов ядрами и
протонами, т. е. нейтронизация вещества.
Ясно, что процесс нейтронизации будет
содействовать Г. к., поскольку при захвате
электронов снижается электронное давление,
а также уносится из звезды в виде нейтрино
определённая энергия. Заметим, что внутри
маломассивной звезды давление вырожденного
газа электронов - осн. часть
давления вещества (см. начало траектории СС`
на рис. 2). Г. к. маломассивных звёзд
отличается от Г. к. массивных звёзд ещё в
одном отношении. После "сгорания"
гелия и образования углеродно-кислородного
ядра звезды (рис. 1) её дальнейшая эволюция
протекает различно в зависимости от массы
образовавшегося ядра. Г. к. массивных звёзд,
с ![]() , развивается (после образования
железного ядра звезды) так, как было описано
на примере Г. к. звёзд с
, развивается (после образования
железного ядра звезды) так, как было описано
на примере Г. к. звёзд с ![]() и с
и с ![]() . В
маломассивных звёздах, с
. В
маломассивных звёздах, с ![]() , Г. к.
может начаться раньше, при выгорании
углерода. Расчёты показывают, что это
выгорание протекает, как правило, бурно, с
нарушением гидростатич. равновесия звезды
и переходит в термоядерный взрыв с большим
выделением энергии.
, Г. к.
может начаться раньше, при выгорании
углерода. Расчёты показывают, что это
выгорание протекает, как правило, бурно, с
нарушением гидростатич. равновесия звезды
и переходит в термоядерный взрыв с большим
выделением энергии.
Однако, несмотря на взрывное горение
углерода и кислорода, этот сложный процесс
в конечном счёте может привести всё-таки к
развитию Г. к., а не к взрыву звезды. Этому
способствуют интенсивная нейтронизация
продуктов горения (ядер группы железа) и
сопровождающие её значит. потери энергии за
счёт нейтринного излучения. Интенсивность
указанных процессов быстро растёт с
увеличением плотности в центре звезды. Из
расчётов следует, что термоядерный взрыв
углеродно-кислородной звезды
действительно переходит в Г. к., если центр.
плотность звезды до начала выгорания
превышает значение rс »1010 г/см3.
Принципиальная возможность Г. к. также
вытекает из сравнения чандрасекаровского
предела для железной звезды (![]() ) н массы
рассматриваемой углеродно-кислородной
звезды (
) н массы
рассматриваемой углеродно-кислородной
звезды (![]() ). Превышение массы последней
над чандрасекаровским пределом явл.
необходимым условием Г. к., а
). Превышение массы последней
над чандрасекаровским пределом явл.
необходимым условием Г. к., а ![]() г/см3 -
достаточным условием.
г/см3 -
достаточным условием.
 |
|
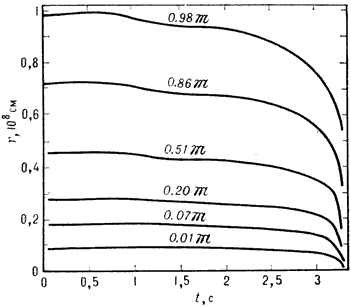
Рис. 4. Изменение со временем радиусов
слоев |
Превращение термоядерного взрыва в Г. к. иллюстрирует рис. 4, где изображено изменение со временем радиусов неск. слоев углеродно-кислородной звезды (траектория её центр, точки СС` дана на рис. 2). В момент времени t = 3,3 с (время отсчитывается от момента, когда темп-pa в центре звезды достигла значения 6.108К, достаточного для развития взрывного термоядерного горения углерода) радиусы всех слоев резко уменьшаются, что и означает переход взрыва в Г. к.
Развивающийся Г. к. сопровождается всё
возрастающим потоком нейтринного излучения, к-рый, частично передавая свою
энергию веществу внеш. слоев звезды,
значительно ускоряет термоядерное горение
остатков углерода в этих слоях. Формируется
мощная детонац. волна с положит. скоростями
вещества позади фронта, достаточными для
отрыва наружной оболочки. Детальный учёт
этого механизма в расчётах и показывает, что
разлетающейся оболочке передаётся энергия
~1050 эрг.
Затем кинетич. энергия оболочки может
увеличиться (но уже в гораздо более
медленном темпе, за 105-106 с) за счёт
эффектов вращения и давления магн. поля до
величины ~1031 эрг, что соответствует энергии
оболочки типичной сверхновой звезды. Если в
углеродно-кислородной звезде центральная
плотность докритическая (![]() г/см3), то
при термоядерном горении в ней может или
спокойно образоваться железное ядро в
результате выгорания части вещества, или
развиться пульсационный режим
термоядерного горения углерода с
последующим взрывом звезды. Теория
эволюции звёзд показывает, что различие в
значениях центр. плотности углеродно-кислородных
звёзд, определяющее их дальнейшую судьбу,
может быть вызвано условиями развития
звёзд в составе тесных двойных систем.
г/см3), то
при термоядерном горении в ней может или
спокойно образоваться железное ядро в
результате выгорания части вещества, или
развиться пульсационный режим
термоядерного горения углерода с
последующим взрывом звезды. Теория
эволюции звёзд показывает, что различие в
значениях центр. плотности углеродно-кислородных
звёзд, определяющее их дальнейшую судьбу,
может быть вызвано условиями развития
звёзд в составе тесных двойных систем.
5. Вспышки сверхновых звёзд, статистика коллапсирующих звёзд, возможности наблюдений
Теория Г. к. приводит, следовательно, к
выводу, что со вспышками сверхновых связан
коллапс маломассивных углеродно-кислородных
звёзд, с массой ок. ![]() . Дополнит. анализ
показывает, что Г. к. с образованием горячей
нейтронной звезды и выбросом (в два этапа)
внеш. оболочки можно отождествить со
сверхновыми I типа. В то же время взрыв
звезды без образования нейтронной звезды
можно поставить в соответствие со
сверхновыми II типа. Следует всё же заметить,
что такие отождествления не вполне
однозначны и не исключают др. вариантов.
Теоретически возможен Г. к. без вспышки
сверхновой, как это было установлено в
расчётах Г. к. массивных железных ядер звёзд.
При этом процессе Г. к. может завершаться
рождением нейтронных звёзд или чёрных дыр.
. Дополнит. анализ
показывает, что Г. к. с образованием горячей
нейтронной звезды и выбросом (в два этапа)
внеш. оболочки можно отождествить со
сверхновыми I типа. В то же время взрыв
звезды без образования нейтронной звезды
можно поставить в соответствие со
сверхновыми II типа. Следует всё же заметить,
что такие отождествления не вполне
однозначны и не исключают др. вариантов.
Теоретически возможен Г. к. без вспышки
сверхновой, как это было установлено в
расчётах Г. к. массивных железных ядер звёзд.
При этом процессе Г. к. может завершаться
рождением нейтронных звёзд или чёрных дыр.
К сожалению, пока трудно сказать что-либо
определённое об относит. частоте различных
исходов эволюции звёзд, и в частности о
частоте Г. к. Существующая статистика звёзд
утверждает, что число звёзд с ![]() ,
оканчивающих свою ядерную эволюцию, растёт
с уменьшением
,
оканчивающих свою ядерную эволюцию, растёт
с уменьшением ![]() как
как ![]() . В Галактике,
согласно этой статистике, для
. В Галактике,
согласно этой статистике, для ![]() число "умирающих" звёзд за год
составляет »1. Но статистика не учитывает
процессов потери массы звёздами в ходе
эволюции, а также ряд др. важных эффектов,
она, вероятнее всего, преувеличивает
частоту Г. к. В то же время вывод о
преобладающем вкладе звёзд малых масс в
число звёзд, завершающих эволюцию гравитац.
коллапсом, кажется правдоподобным. Кроме
того, следует подчеркнуть, что масса звезды,
о к-рой идёт речь в теории поздних стадий
эволюции, на самом деле представляет собой
массу углеродно-кислородного ядра звезды,
имеющей гетерогенную структуру гиганта с
плотным ядром и разреженной оболочкой. Из
расчётов эволюции звёзд известно, что масса
ядра в неск. раз меньше массы всей звезды (напр.,
масса ядра, равная
число "умирающих" звёзд за год
составляет »1. Но статистика не учитывает
процессов потери массы звёздами в ходе
эволюции, а также ряд др. важных эффектов,
она, вероятнее всего, преувеличивает
частоту Г. к. В то же время вывод о
преобладающем вкладе звёзд малых масс в
число звёзд, завершающих эволюцию гравитац.
коллапсом, кажется правдоподобным. Кроме
того, следует подчеркнуть, что масса звезды,
о к-рой идёт речь в теории поздних стадий
эволюции, на самом деле представляет собой
массу углеродно-кислородного ядра звезды,
имеющей гетерогенную структуру гиганта с
плотным ядром и разреженной оболочкой. Из
расчётов эволюции звёзд известно, что масса
ядра в неск. раз меньше массы всей звезды (напр.,
масса ядра, равная ![]() , соответствует
полной массе звезды
, соответствует
полной массе звезды ![]() ). Пока трудно
указать значение наименьшей массы
коллапсирующих звёзд, но оно, очевидно,
должно превышать чандрасекаровский предел
железной звезды (
). Пока трудно
указать значение наименьшей массы
коллапсирующих звёзд, но оно, очевидно,
должно превышать чандрасекаровский предел
железной звезды (![]() ).
).
Если масса горячей нейтронной звезды
![]() такая нейтронная звезда после
короткого периода интенсивного
нейтринного охлаждения (неск. десятков
секунд) не должна испытывать
релятивистской Г. к. и может наблюдаться в
виде источника постепенно ослабевающего
теплового рентг. излучения, а также долгое
время в виде пульсара с излучением в
диапазоне от радиоволн до гамма-лучей.
такая нейтронная звезда после
короткого периода интенсивного
нейтринного охлаждения (неск. десятков
секунд) не должна испытывать
релятивистской Г. к. и может наблюдаться в
виде источника постепенно ослабевающего
теплового рентг. излучения, а также долгое
время в виде пульсара с излучением в
диапазоне от радиоволн до гамма-лучей.
В теории Г. к. особенно интересен вопрос о
нейтринном излучении. В ходе Г. к.
излучаются в виде импульса
продолжительностью 10-30 с нейтрино v и
антинейтрино ![]() с полной энергией »3.1053 эрг. В
первом приближении можно считать, что v и
с полной энергией »3.1053 эрг. В
первом приближении можно считать, что v и
![]() в
этом импульсе представлены в примерно
равных количествах, причём энергия
отдельной частицы в среднем составляет 10-15
МэВ. Расчётная кривая нейтринной
светимости
в
этом импульсе представлены в примерно
равных количествах, причём энергия
отдельной частицы в среднем составляет 10-15
МэВ. Расчётная кривая нейтринной
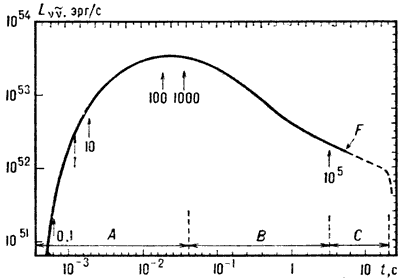
светимости ![]() звезды с массой
звезды с массой ![]() изображена на рис. 5. Начало отсчёта времени
выбрано произвольно, когда ср. оптическая
толща звезды
изображена на рис. 5. Начало отсчёта времени
выбрано произвольно, когда ср. оптическая
толща звезды ![]() . Значения оптич. толщи
. Значения оптич. толщи
![]() указаны около вертикальных стрелок. Осн.
часть кривой нейтринной светимости
соответствует условиям нейтринной
непрозрачности ядра звезды (
указаны около вертикальных стрелок. Осн.
часть кривой нейтринной светимости
соответствует условиям нейтринной
непрозрачности ядра звезды (![]() ). Точка F
указывает момент прекращения гидродинамич.
расчёта Г. к. Буквами А, В и С обозначены
различные фазы Г. к., к-рые характеризуются
следующими данными:
). Точка F
указывает момент прекращения гидродинамич.
расчёта Г. к. Буквами А, В и С обозначены
различные фазы Г. к., к-рые характеризуются
следующими данными:
| A | B | C | |
| 1 | 17 | 30 | |
| 12 | 14 | 15 | |
| Dt, c | 0,04 | 3,1 | 15 |
Здесь ![]() - полная энергия всех сортов
нейтрино, включая электронные и мюонные;
- полная энергия всех сортов
нейтрино, включая электронные и мюонные; ![]() - ср. энергия нейтрино и антинейтрино; Dt
- продолжительность соответствующей фазы Г.
к.
- ср. энергия нейтрино и антинейтрино; Dt
- продолжительность соответствующей фазы Г.
к.
 |
|
Рис. 5. Изменение нейтринной светимости |
Значит. длительность нейтринного свечения объясняется тем, что осн. доля энергии излучается не в процессе быстрой гидродинамич. стадии Г. к., а на последующей стадии аккреции вещества внеш. слоев (фаза В, рис. 5) и охлаждения горячей гидростатически равновесной нейтронной звезды (фаза С). Нейтринный импульс, излучённый коллапсирующей в пределах нашей Галактики звездой, в принципе может быть зарегистрирован на имеющихся уже детекторах нейтринного излучения (см. Нейтринная астрономия). Обнаружение нейтринного импульса стало бы непосредственной наблюдательной проверкой теории Г. к. В частности, оно позволило бы проверить важный вывод теории о возможности Г. к., протекающего без сброса оболочки и, следовательно, без наблюдаемых эффектов типа вспышек сверхновых. Таких процессов в Галактике может происходить, как уже говорилось, »1 в год.
В процессе Г. к. звёздных ядер с массой, не
превышающей массу холодной нейтронной
звезды (![]() ), эффекты общей теории
относительности (ОТО) не очень существенны,
хотя их нужно будет учитывать при
последующем развитии теории Г. к. Однако
эффекты ОТО имеют решающее значение для
релятивистского Г. к., к-рым заканчивается
эволюция массивных звёздных ядер.
), эффекты общей теории
относительности (ОТО) не очень существенны,
хотя их нужно будет учитывать при
последующем развитии теории Г. к. Однако
эффекты ОТО имеют решающее значение для
релятивистского Г. к., к-рым заканчивается
эволюция массивных звёздных ядер.
Лит.: Зельдович Я. Б., Новиков П. Д., Теория тяготения и эволюция звезд, М., 1971; Шкловский И. С., Сверхновые звезды и связанные с ними проблемы, 2 изд., М., 1976, с. 398 и посл.; На переднем крае астрофизики, пер. с англ., М., 1979; Имшенник В. С., Надежин Д. К., Конечные стадии эволюции звезд и вспышки сверхновых, в кн.: Итоги науки н техники. Сер. Астрономия, т. 21, М., 1982.
(В.С. Имшенник)
В. С. Имшенник, "Физика Космоса", 1986
Глоссарий Astronet.ru
|
Публикации с ключевыми словами:
гравитационный коллапс
Публикации со словами: гравитационный коллапс | |
|
См. также:
| |