Астронет > Неустойчивости плазмы

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

На сайте

Астрометрия

Астрономические инструменты

Астрономическое образование

Астрофизика

История астрономии

Космонавтика, исследование космоса

Любительская астрономия

Планеты и Солнечная система

Солнце

Неустойчивости плазмы

1. Введение
2. Магнитогидродинамические неустойчивости
3. Кинетические неустойчивости
4. Параметрические неустойчивости

1. Введение

Одной из наиболее важных особенностей плазмы явл. возможность существования и распространения в ней различных типов колебаний и волн. Можно сказать, что плазма представляет собой не только совокупность большого числа заряженных частиц, но также и ансамбль большого числа осцилляторов - собственных колебаний, характеризующихся определёнными значениями волнового вектора и частоты. В равновесной плазме уровень этих колебаний весьма мал, это т.н. тепловые флуктуации. Резко отличная ситуация имеет место при отклонении состояния плазмы от равновесного (электрич. ток в плазме, пучок быстрых частиц и т.д.), когда становится возможным развитие Н. п., т.е. нарастания малых возмущений в плазме до высокого уровня.

2. Магнитогидродинамические неустойчивости

Наиболее радикальными Н. п., приводящими к макроскопич. перемещениям больших участков плазмы, явл. т.н. магнитогидродинамические (МГД) неустойчивости. В зависимости от того, развиваются ли Н. п. за времена, существенно меньшие или сравнимые с характерным временем между соударениями частиц, говорят об идеальных или диссипативных МГД-неустойчивостях.

Из идеальных наиболее существенными явл. желобковая и винтовая Н. п. Возникновение желобковой Н. п. связано с тем, что плазма, как всякий диамагнетик, стремится перемещаться в сторону более слабых магн. полей. В результате отдельные трубки силовых линий будут "всплывать" вместе с заключённой в них плазмой в сторону более слабого поля. Для того чтобы получить критерий неустойчивости, рассмотрим магн. трубку, образованную тонким пучком силовых линий. Объём этой трубки $V =\oint S\;dl$ , где S - поперечное сечение трубки, а интеграл берётся вдоль силовых линий. Плазма, заполняющая трубку, стремится расшириться, но при всяких перемещениях трубки магнитный поток Ф = SB (В - напряжённость магн. поля) в ней должен сохраняться. Поэтому плазма будет перемещаться в сторону увеличения т.н. удельного объёма магн. трубки $U=\oint dl/B$ . Граница плазмы в магн. поле будет устойчива лишь в том случае, когда при смещении её в область, занятую только магн. полем, выполняется условие $\delta U < 0$ . В противном случае плазма как бы стремится поменяться местами с магн. полем (отсюда другой термин - конвективная, или перестановочная, неустойчивость). Возмущения поверхности плазмы при этой неустойчивости будут иметь вид желобков, ориентированных вдоль силовых линий.

Если в случае желобковой Н. п. освобождается тепловая энергия, заключённая в плазме, то в случае винтовой Н. п. энергетич. резервуаром для развития неустойчивости служит магн. поле. Простейшая конфигурация, в к-рой возможна винтовая Н. п., - это плазменный шнур с винтовыми силовыми линиями магн. ноля. Неустойчивость развивается в результате того, что силовые линии, стремясь сократиться аналогично резиновым жгутам, деформируют шнур таким образом, чтобы их кривизна уменьшалась. Винтовая Н. п. может быть подавлена при наложении достаточно сильного продольного (вдоль шнура) магн. поля.

В условиях, когда винтовая Н. п. подавлена, в плазме с конечной проводимостью развивается диссипативный аналог винтовой Н. п., при к-ром происходит разрыв силовых линий магн. поля. Эта разновидность Н. п. получила название разрывной неустойчивости или тиринг-неустоичивости (от англ. tearing - разрыв). Наиболее важной явл. разрывная неустойчивость в плазме с нейтральным слоем, по обе стороны от к-рого силовые линии магн. поля имеют противоположное направление. Такой скачок магн. поля поддерживается током в слое. Т.к. сила притяжения между отдельными токовыми нитями растёт при их сближении, а связь этих нитей с остальными нитями ослабляется из-за удаления, то плоский токовый слой разбивается на отдельные жгуты. При этом происходит перестройка конфигурации магн. поля: часть магн. силовых линий, направленных первоначально вдоль слоя, перезамыкается вокруг токовых жгутов. Избыток энергии магн. поля передаётся плазме. Перезамыкание возможно при наличии конечной диссипации в плазме, когда нарушается вмороженность магн. поля (см. Магнитогидродинамика). В бесстолкновительной плазме такая диссипация обусловлена черенковским взаимодействием тиринг-моды с резонансными частицами плазмы в нейтральном слое.

Тиринг-неустойчивость - наиболее существенная Н. п. в астрофизике. В частности, она, по-видимому, отвечает за высвобождение энергии магн. поля магнитосферного хвоста Земли.

3. Кинетические неустойчивости

Кроме МГД-неустойчивостей в плазме могут возбуждаться колебания, для к-рых явл. существенным взаимодействие с отдельными группами частиц (резонансные частицы). Такие Н. п. наз. микро- или кинетич. неустойчивостями.

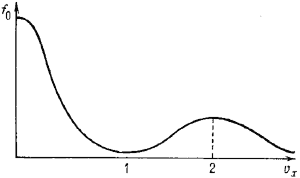
Рис. 1. Функция распределения электронов
плазмы и пучка по составляющей скорости
в направлении движения пучка.

В основе кинетич. Н. п. лежит возбуждение колебаний или волн отдельными группами резонансных частиц, к-рые в неравновесной плазме могут служить энергетич. резервуаром для неустойчивости. Макроскопич. проявления кинетич. неустойчивостей - возбуждение в плазме интенсивных колебаний (чаще всего шумового характера), обусловленная неустойчивостью релаксация неравновесных распределений частиц и, наконец, влияние на процессы переноса в плазме (электрич. ток, диффузию, теплопроводность).

Наиболее простой тип кинетич. Н. п. развивается при взаимодействии с плазмой пучков заряженных частиц. Этот подкласс кинетич. Н. п. получил название пучковых. Проще всего интерпретировать пучковую неустойчивость как обращение эффекта затухания Ландау. При наличии в плазме достаточно интенсивного пучка электронов функция распределения по скоростям f₀ имеет второй максимум при скорости, соответствующей ср. скорости частиц пучка v₀ (точка 2 на рис. 1). В этом случае всегда существует интервал скоростей резонансных частиц между точками 1 и 2 на рис. 1, в к-ром производная $\partial f_0/\partial v_x > 0$ . Волны, фазовые скорости к-рых лежат в этом интервале, будут поглощать энергию пучка, а их амплитуды нарастать со временем (см. Ландау затухание). Т.о., из широкого спектра плазменных колебаний, возникающих вследствие тепловых флуктуации, выделяется узкий спектральный интервал волн, находящихся в резонансе с пучком и поглощающих его энергию. Развитие пучковой Н. п. сопровождается разбиением электронного пучка на сгустки и группировкой его частиц в области тормозящих фаз электрич. поля неустойчивой плазменной волны. Рассмотрим плазменную волну, распространяющуюся в направлении движения пучка и имеющую фазовую скорость v_ф, близкую к его ср. скорости v₀. В системе отсчёта волны электрич. поле, действующее на пучок, квазистационарно и энергия электронов $m_e (v-v_ф)^2/2 - e\varphi$ ( $\varphi$ - электростатич. потенциал в волне) должна сохраняться. Поэтому изменение скорости ( $v=v_0+\delta v$ ) электронов $\delta v\sim e\varphi/m_e (v_0-v_ф)$ . Если волна движется несколько медленнее пучка (v₀ > v_ф), то группировка частиц должна иметь место в той области фаз, где $\partial\varphi/\partial x < 0$ , т.е. сила электрич. 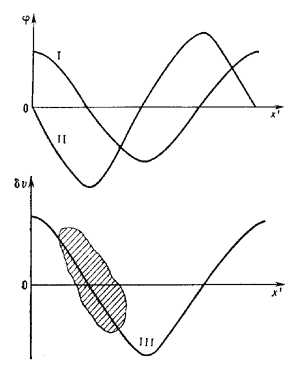поля волны, действующая на электроны пучка $e\partial\varphi/\partial x < 0$ , явл. тормозящей (рис. 2). Электроны, группируясь в области тормозящих фаз поля, отдают энергию волне и тем самым ещё больше усиливают модулирующую их плазменную волну. Развивается пучковая Н. п. - экспоненциально быстрое нарастание плазменных колебаний с теплового уровня, сопровождающееся модуляцией пучка.

Рис. 2. Автомодуляция пучка при пучковой
неустойчивости. I - график
электростатического потенциала в волне
$\varphi=\varphi_0\cos kx'$ ; II - сила, действующая
на электроны пучка $e\partial\varphi/\partial x$ ;
III - изменение скорости электронов
пучка ( $\delta v$ ) в поле волны при v₀ > v_ф.
Графики приведены в системе отсчёта волны:
x' = x - v_фt. Положительное значение
$\delta v$ соответствует движению частиц
вправо, отрицательное - влево. Частицы
скапливаются (группируются) в
заштрихованной области.

Обычно при пучковой Н. п. энергия плазменных колебаний, возбуждаемых пучком, сравнима с его начальной энергией. Однако в случае интенсивных пучков могут стать существенными эффекты нелинейного взаимодействия плазменных волн друг с другом, перекачивающие энергию в область спектра, где эти волны непосредственно с пучком не взаимодействуют. В этом случае стабилизация (прекращение роста) неустойчивости происходит при уровнях энергии плазменных волн, существенно меньших энергии пучка (см. Плазменная турбулентность).

В космич. условиях пучковая Н. п. возникает часто. Напр., образующиеся при вспышках на Солнце быстрые частицы, проходя через солнечную корону, возбуждают в ней плазменные колебания, энергия к-рых затем трансформируется в эл.-магн. волны. Эти волны наблюдаются в виде солнечных радиовсплесков III типа (см. Радиоизлучение Солнца).

Не менее распространённой в космич. условиях явл. циклотронная Н. п., в основе к-рой лежит возбуждение волн резонансными частицами при нормальном и аномальном эффекте Доплера. Условие резонансного взаимодействия волн и частиц при нормальном эффекте Доплера ( $\omega-k_{||}v_{||}=\omega_н$ ) означает, что частота волн со с учётом доплеровского сдвига $\Delta\omega=\omega v_{||}/c=k_{||}v_{||}$ Гц (т.е. в системе K, движущейся вместе с частицей со скоростью v_||) совпадает с циклотронной частотой $\omega_н$ (k_|| - проекция волнового вектора на направление внешнего магн. поля, v_|| - компонент скорости вдоль поля). В этом случае излучение волн происходит за счёт энергии поперечного движения заряженной частицы. При резонансе, связанном с аномальным эффектом Доплера ( $\omega-k_{||}v_{||}=-\omega_н$ ), вектор электрич. поля в волне и частица вращаются в противоположных направлениях. В этом случае резонанс возможен только при достаточно большом доплеровском сдвиге частоты, изменяющем направление вращения электрич. вектора волны (в системе K) на противоположное; излучение происходит за счёт энергии продольного движения частицы.

При циклотронной Н. п. возможно возбуждение эл.-магн. волн, в частности вистлеров, распространяющихся вдоль магн. поля, МГД-волн (альвеновских, магнитозвуковых) и др. Как и пучковая, циклотронная Н. п. сопровождается фазовой группировкой резонансных частиц (происходящей в направлении распространения волны), при к-рой резонансные частицы собираются в основном в области тормозящих фаз и усиливают взаимодействующую с ними волну. Отличие от пучковой Н. п. лишь в том, что в случае циклотронной неустойчивости эл.-магн. волны группировка связана с действием на частицы продольного компонента силы Лоренца $[{\bf v}_\perp {\bf H}_\perp]e/c$ , ${\bf H}_\perp$ - магн. поле волны, ${\bf v}_\perp$ - скорость резонансной частицы поперёк внешнего магн. поля. Циклотронная Н. п. возникает не только при наличии пучка в плазме, но и в том случае, когда резонансные частицы имеют анизотропное распределение по скоростям, т.е. когда их распределение по скоростям вдоль магн. поля не повторяет распределение по поперечным скоростям. Именно такая ситуация имеет место в геомагнитной ловушке, как и в любой ловушке с магн. пробками (см. Магнитосферы планет). Те заряженные частицы, к-рые движутся приблизительно вдоль магн. поля, проходят сквозь пробку и теряются в атмосфере, а частицы с большими поперечными скоростями, т.е. движущиеся под большими "питч-углами" к полю, отражаются от магн. пробки и не достигают атмосферы. В результате в системе оказывается недостаток частиц, движущихся вдоль поля, распределение быстрых частиц но скоростям становится анизотропным и возникают условия для развития циклотронной Н. п.

В плазме с анизотропным распределением по скоростям может развиваться т.н. шланговая неустойчивость. Физ. механизм этой Н. п. легче всего понять, если рассмотреть альвеновские волны в анизотропной плазме. Известно, что альвеновские волны представляют собой колебания упругих нитей - силовых линий магн. поля. Поскольку в бесконечно проводящей плазме частицы привязаны к силовым линиям, то при искривлении силовой линии возникает центробежная сила, пропорциональная энергии продольного (вдоль силовой линии) движения частиц и стремящаяся увеличить искривление. В анизотропной плазме с большой продольной темп-рой $k(T_{||}-T_\perp)> H^2/4\pi n$ - темп-ры, характеризующие движение частиц плазмы вдоль и поперёк магн. поля, n - концентрация заряженных частиц в плазме) эта сила оказывается больше, чем возвращающие силы, связанные с натяжением силовых линий и с диамагнитными св-вами плазмы. В результате силовая линия будет еще больше искривляться по аналогии с поведением шланга, по к-рому подаётся сильная струя воды. Неустойчивость рассматриваемого типа возможна в плазме солнечного ветра, с ней связана диссипация на фронте межпланетных ударных волн.

Наконец, в космич. плазме весьма существенной оказывается токовая Н. п. Относит. движение электронов и ионов при протекании тока сходно с движением пучка через плазму и приводит к развитию неустойчивости, аналогичной пучковой. В результате токовой Н. п. возбуждаются ионно-звуковые, ионно-плазменные колебания, а при токовых скоростях электронов, больших тепловой скорости, - и более высокочастотные волны. Осн. макроскопич. следствие токовой Н. п. - быстрая передача импульса электронов колебаниям и участвующим в колебаниях ионам, т.е. возникновение аномального сопротивления. С аномальным сопротивлением, по-видимому, связано существование двойных слоев - скачков потенциала, возникающих при протекании тока. В таких слоях на расстоянии неск. дебаевских радиусов электроны ускоряются до энергий, существенно превышающих тепловую. Двойные слои неоднократно наблюдались в лабораторной плазме, они возникают также в авроральных областях магнитосферы Земли и существенны при установлении магнитосферно-ионосферных связей. Токовые Н. п. имеют место и на фронтах бесстолкновительных ударных волн, где из-за резкого изменения магн. поля возникает сильное электрич. поле, в к-ром электроны плазмы приобретают большую направленную скорость. В частности, токовая Н. п. и возбуждение плазменных волн должны иметь место на фронтах ударных волн, образованных вспышками на Солнце. Превращение плазменных волн в электромагнитные вызывает солнечные радиовсплески II типа.

4. Параметрические неустойчивости

При распространении в плазме эл.-магн. волны большой амплитуды имеет место периодич. пространственно-временная модуляция параметров плазмы. На фоне такой модуляции возникает параметрич. связь волн малой амплитуды (пробные волны), и амплитуда этих волн нарастает со временем по экспоненциальному закону. Причиной раскачки пробных волн явл. колебания электронов и ионов плазмы в поле эл.-магн. волны большой амплитуды (волны накачки). Неустойчивости такого типа называются параметрическими.

Наиболее простым примером параметрич. Н. п. явл. распадная неустойчивость волн - эффект, в значит. степени аналогичный параметрич. резонансу в механике. Суть её заключается в том, что при наличии в плазме волны накачки $a(t, {\bf r})=a\cos({\bf k_0r}-\omega_0 t)$ с волновым вектором k₀ и частотой $\omega_0$ одновременно нарастают две волны с частотами и волновыми векторами $\omega_1$ , k₁ и $\omega_2$ , k₂, удовлетворяющими следующим условиям параметрич. резонанса (распадным условиям): $\omega_0=\omega_1+\omega_2$ , k₀=k₁ + k₂. Рассматривая колебания плазмы как газ квазичастиц, обладающих энергией $\hbar \omega$ и импульсом $\hbar$ k, можно наглядно интерпретировать распадные условия как законы сохранения энергии и импульса при распаде кванта с энергией $\hbar \omega_0$ и импульсом $\hbar$ k₀ на два других ( $\hbar\omega_1$ , $\hbar$ k₁) и ( $\hbar\omega_2$ , $\hbar$ k₂). Поскольку при распаде энергия передаётся обоим образующимся квантам, то они должны иметь меньшие частоты, чем квант волны накачки: $\omega_0 > \omega_1, \omega_2$ . Если волна накачки и пробные волны принадлежат одной и той же ветви дисперсионной кривой колебаний, то распадные условия выполняются далеко не для всякой зависимости $\omega$ (k) (см. Плазма). Гораздо проще удовлетворить распадным условиям, если в процесс параметрич. неустойчивости вовлечены неск. ветвей колебаний. Так, напр., для ленгмюровской волны накачки выполнение распадных условий возможно при её распаде на ленгмюровскую и ионно-звуковую волны (сокращённо $l\to l'+s$ ). Соответствующая параметрич. неустойчивость стала первым типом распада волн в плазме, предсказанным и исследованным в 1962 г. Р.3. Сагдеевым и В.Н. Ораевским. Механизм связи ленгмюровских и ионно-звуковых колебаний следующий. При наличии в неизотермической ( $T_e\gg T_i$ , где Т_е, Т_i - темп-ры электронов и ионов плазмы) плазме ионно-звуковой волны ленгмюровские колебания происходят на фоне медленных вариаций плотности плазмы, вызванных такой волной. Поскольку число ленгмюровских квантов $\sim W/\omega_p$ [ $W=E^2/4\pi$ - плотность энергии ленгмюровских колебании, Е - амплитуда колебаний электрич. поля в ленгмюровской волне, $\omega_p=(4\pi e^2 n_0/m_e)^{1/2}$ - их частота, n₀ - концентрация электронов] должно сохраняться, то модуляция плотности плазмы сопровождается модуляцией интенсивности ленгмюровских колебаний. Это приводит к возникновению силы высокочастотного давления ленгмюровских колебаний (давление "газа" ленгмюровских квантов), изменяющей плотность плазмы и таким образом осуществляющей их обратную связь с ионно-звуковыми колебаниями. При заданной амплитуде электрич. поля волны накачки E₀= const инкремент нарастания $\gamma_d$ (величина, обратная времени возрастания амплитуды в е раз) амплитуды пробных волн равен:
$\gamma_d=\sqrt{\omega_p\omega_s}\cdot\sqrt{E_0^2\over{64\pi n_0 kT_e}}$
где $\omega_s=k(kT_e/m_i)^{1/2}$ - частота ионно-звуковых колебаний (m_i - масса иона). При наличии диссипации энергии пробных ленгмюровской и ионно-звуковой волн, обусловленной столкновениями или затуханием Ландау, распадная неустойчивость возникает только при амплитудах волны накачки выше пороговой. Порог для возникновения неустойчивости определяется из условия $\gamma_d^2 > \gamma_l \gamma_s$ - декременты затухания (величины, обратные времени уменьшения амплитуды в е раз) ленгмюровской и ионно-звуковой волн. Отличное от нуля пороговое значение амплитуды волны накачки возникает также в неоднородной плазме за счёт конвективного сноса колебаний из области резонансного взаимодействия.

Кроме рассмотренной выше распадной неустойчивости ленгмюровской волны $l\to l'+s$ в плазме возможно большое число др. распадных неустойчивостей, связывающих различные типы колебаний.

Интересная особенность распадной неустойчивости в неравновесной плазме связана с наличием в ней волн с отрицат. энергией. "Отрицательность" энергии волны означает, что возбуждение волны сопровождается уменьшением, а не увеличением волновой энергии среды. Это возможно в плазме с неравновесным распределением частиц по скоростям (пучок в плазме, анизотропия темп-р и др.). Взаимодействие такой волны с волнами положит. энергии приводит к возникновению параметрич. неустойчивости взрывного типа. Причина её состоит в том, что, отдавая в процессе распада свою энергию пробным волнам, волна накачки увеличивает, а не уменьшает свою амплитуду. Развивающаяся при этом "нелинейная" неустойчивость характеризуется тем, что её инкремент тем больше, чем большего уровня достигла амплитуда. Т.о., неустойчивость носит характер взрыва, когда за малое время амплитуда волны нарастает до больших значений.

При достаточно больших амплитудах волны накачки инкремент распадной неустойчивости $l\to l'+s$ $$\omega_l(k)=\omega_p \left(1+{\delta n\over{2n_0}}\right) (D - дебаевский радиус, n0 - невозмущённая плотность плазмы) следует, что в$ превышает частоту ионно-звуковых колебаний. При таких амплитудах align="absmiddle" width="18" height="13" >) частота (энергия) плазмонов - квантов ленгмюровских + {2\over 3} k^2 D^2 \omega_p$" align="absmiddle" width="229" height="30" > 005/01/15/0001202032/tex/formula42.gif" border="0" alt="$\delta n$" align="absmiddle" width="18" height="13" > >). Т.о., области пониженной плотности плазмы играют роль потенциальных

Лит. см. при ст. Ландау затухание.

(В.И. Шевченко)

В. И. Шевченко, "Физика Космоса", 1986
Глоссарий Astronet.ru

А | Б | В | Г | Д | З | И | К | Л | М | Н | О | П | Р | С | Т | У | Ф | Х | Ц | Ч | Ш | Э | Я

Публикации с ключевыми словами: плазменные неустойчивости Публикации со словами: плазменные неустойчивости
См. также: Неустойчивости плазмы

Обсудить эту публикацию

Версия для печати