Ценный дар небесной механики
15.03.2001 16:41 | Л.В. Ксанфомалити/Вселенная и Мы

Недостижимость Солнца в простейшей схеме космического полета представляется достаточно очевидной. Ясно, что если погасить скорость тела, которую ему сообщает орбитальное движение Земли, оно упадет на Солнце. Только чем ее можно

погасить? Орбитальная скорость Земли, 30 км/с, намного превосходит возможности ракет на химических источниках энергии (около 18 км/с). Существуют подобные же ограничения на полет к Меркурию, хотя они и менее суровы. Мне самому часто приходилось объяснять это слушателям в Московском планетарии. Тем не менее, кое-что оказалось для меня новым, когда в 1974 г. автор проекта траектории полета к Меркурию аппарата Маринер-10 Дж. Коломбо приехал в Москву и выступил в Институте космических исследований с докладом.

Плодотворная идея

Два взаимосвязанных аспекта доклада Дж. Коломбо произвели на меня большое впечатление:

использование гравитационного поля Венеры для достижения Меркурия, и то, что без всяких усилий со стороны проектантов орбита Маринера-10 обеспечивает, после сближения с планетой 29 марта 1974 г., систематические возвращения аппарата в точку первого сближения, причем со строгой периодичностью ровно в 2 меркурианских года. (Из-за ограниченных запасов рабочего тела в системе ориентации для исследований удалось использовать только два последующих сближения, 21 сентября 1974 г. и 16 марта 1975 г.). Для самих проектантов это оказалось полной неожиданностью, рассказывал Дж. Коломбо; планировалось лишь одно сближение, а этот странный результат был получен, когда в ответ на вопрос - что будет с аппаратом после сближения - расчетная программа выдала эти удивительные свойства орбиты Маринера-10 , которые вначале даже посчитали ошибкой.

Сейчас ясно, что эти свойства связаны с вековыми резонансами и другими соизмеримостями, которыми насквозь пронизана Солнечная система и которые впервые почувствовал и несколько своеобразно описал еще Иоганн Тициус, профессор Виттенбергского университета, в 1766 г. (Как известно, благодарные потомки присвоили его открытию имя другого Иоганна - Боде). Но вернемся к нашей теме.

Параметры орбиты Маринера-10 определялись тремя планетами: Землей, Меркурием и Венерой. Орбита была сформирована с помощью впервые тогда использованного гравитационного маневра. Для этого запущенный аппарат вначале был направлен к Венере. Это позволило решить проблему сближения с Меркурием, имеющим среднюю орбитальную скорость 48 км/с (и максимальную 54 км/с).

Использование гравитационных маневров - тема настоящей статьи. Они позволяют значительно увеличить научную нагрузку космических аппаратов и очень заметно сократить время достижения цели. Так, длительность широко известной миссии Вояджера-2 с ее многочисленными маневрами, охватившей все планеты-гиганты, составила всего 12 лет, в то время как полет по классической (гомановской) траектории к Нептуну длился бы лет 30. Напомним, что гомановская эллиптическая перелетная траектория строится так, чтобы в гелиоцентрических координатах она касалась Земли, находящейся в перигелии, и планеты-цели - в афелии. Для гравитационных маневров необходимо еще одно тело на пути аппарата. Интересно, что в качестве него можно использовать даже Землю, если в проекте предусмотреть возвращение к ней.

Устройство механизма гравитационных маневров относится к той интересной особой части нашего мировосприятия, где сосредоточены известные, но неочевидные понятия, подсознательно отвергаемые нашей интуицией, знание которых почему-то не приводит к немедленному практическому их использованию. (Это свойство психики далеко не ограничивается гравитационными маневрами, таких примеров много; отвлеку читателя на один из самых ярких из моей коллекции. Сразу после того, как в конце 1978 г. с помощью зондов Венера-11 и Венера-12 мы обнаружили электрическую активность атмосферы Венеры, с таким же сообщением выступил покойный ныне профессор Лос-Анжелесского университета Ф.Скарф, который также зарегистрировал это явление, но не с зонда, а со спутника

Пионер-Венера . Его оппоненты выступили с резкой критикой, указывая, что ионосфера экранирует спутник и регистрация низкочастотных сигналов на нем невозможна. Прекрасному специалисту Ф.Скарфу понадобился почти год, чтобы сообразить, как именно сигнал достигает аппарата, хотя лекции о распространении волны вдоль магнитного поля, в моде вистлера, он сам постоянно читал студентам!).

Механика гравитационных маневров

Рис. 1. Скорости аппарата в планетоцентрических (а) и гелиоцентрических (б) координатах.

 

Гравитационный маневр как природное явление впервые был обнаружен астрономами прошлого, которые поняли, что значительные изменения орбит комет, их периода (а следовательно и их орбитальной скорости) происходят под гравитационным влиянием планет. Так, после перехода короткопериодических комет из пояса Койпера во внутреннюю часть Солнечной системы, значительное преобразование их орбит происходит именно под гравитационным влиянием массивных планет, при обмене с ними угловым моментом, без каких-либо энергетических затрат.

Саму идею использовать гравитационный маневр для целей космического полета разработал Майкл Минович в 60-х годах, когда, будучи студентом, он проходил практику в JPL*. Идея была быстро подхвачена и реализована во многих космических миссиях. Но на первый взгляд, возможность значительно ускорить движение аппарата без затрат энергии кажется странной и требует пояснения.

Часто приходится слышать о захвате астероидов и комет полем планет. Строго говоря, захват без потерь энергии невозможен: если какое-то тело приближается к массивной планете, модуль его скорости сначала возрастает по мере приближения, а затем на столько же уменьшается в процессе его удаления. Но тело все же может перейти на орбиту спутника планеты, если при этом происходит его торможение (например, имеется торможение в верхних слоях атмосферы, если сближение достаточно тесное; или если возникает значительное приливное рассеяние энергии; или, наконец, если происходит разрушение тела внутри предела Роша с различными векторами скорости, приобретенными обломками). На стадии формирования Солнечной системы важным фактором было также торможение тела в газо-пылевой туманности. Что же касается космических аппаратов, то только в случае вывода на орбиту спутника используется торможение в верхних слоях атмосферы (aerobraking). В чистом гравитационном маневре правило равенства модуля скоростей до и после сближения с планетой сохраняется неукоснительно (что и подсказывала интуиция: с чем пришел, с тем и ушел). В чем же выигрыш?

Выигрыш становится очевидным, если от планетоцентрических перейти к гелиоцентрическим координатам, что иллюстрирует рис. 1, за основу которого взята диаграмма из книги В.И.Левантовского Механика космического полета . На рис. 1а показана траектория аппарата, как ее видит наблюдатель на планете P. Скорость v^вх на местной бесконечности по модулю равна v_вых. Все, что заметит наблюдатель, это изменение направления движения аппарата. Однако наблюдатель, находящийся в гелиоцентрических координатах, увидит значительное изменение скорости аппарата. Поскольку сохраняется только модуль скорости аппарата относительно планеты, а он сравним с модулем орбитальной скорости самой планеты, результирующая векторная сумма скоростей может стать как большей, так и меньшей скорости аппарата перед сближением. На рис. 1б показана векторная диаграмма такого

обмена угловыми моментами. Через v_вх и v_вых обозначены равные скорости входа и выхода аппарата относительно планеты, а через V_сбл, V_удал и V_пл - скорости сближения и удаления аппарата и орбитальная скорость планеты в гелиоцентрических координатах. Приращение dV - это тот импульс скорости, который планета сообщила аппарату. Конечно,

совершенно пренебрежим момент, который сам аппарат передает планете.

Угол , на который изменилось направление полета в сближении, определяется массой планеты M, прицельной дальностью d и скоростью v_вх. Таким образом, соответствующим выбором трассы сближения можно не только изменить направление, но и значительно увеличить скорость аппарата без всяких затрат его энергоисточников. На рис. 1 не показано, что вначале скорость резко возрастает, а затем падает до конечной величины. Баллистиков это обычно не заботит, они воспринимают обмен угловыми моментами как гравитационный удар со стороны планеты, длительность которого пренебрежимо

мала по сравнению с полной длительностью полета (рис. 3).

Критическими в гравитационном маневре оказываются три последних из перечисленных параметров, а именно, масса планеты, умноженная на гравитационную постоянную M, прицельная дальность d и скорость v_вх. Чем меньше расстояние d до планеты, в сфере действия которой выполняется маневр, тем эффективнее обмен угловыми моментами. Но одновременно увеличивается угол :

Ограничения на расстояние d накладываются реальными размерами планеты и высотой ее атмосферы. Интересно, что приращение скорости dV

оказывается максимальным, когда v_вх равно круговой скорости у поверхности планеты. При этом угол становится равным 60°. И, конечно, обмен тем эффективнее, чем больше масса планеты. В таблице, также заимствованной из книги Левантовского, приведены теоретические максимально возможные приращения скорости аппарата при сближении с планетами и Луной.

Таким образом, наиболее выгодны маневры у планет-гигантов, причем они заметнo сокращают длительность полета. Используются также маневры у Земли и Венеры, но это значительно увеличивает длительность космического путешествия. Все приведенные в таблице данные относятся к пассивному маневру. Но в некоторых случаях в перицентре облетной гиперболы аппарату, с помощью его двигательной установки, сообщают небольшой реактивный импульс, что дает существенный дополнительный выигрыш.

Максимально возможные приращения скорости, км/с

 

В полете аппарату часто требуется не ускорение, а замедление. Из рис. 1 видно, что легко выбрать такую геометрию сближения, когда скорость аппарата в гелиоцентрических координатах упадет. Это зависит от положения векторов скоростей при обмене угловыми моментами. Упрощая задачу, можно сказать, что сближение аппарата с планетой с внутренней стороны ее орбиты приводит к тому, что аппарат отдает планете часть своего углового момента и замедляется; и наоборот, сближение с внешней стороны орбиты приводит к увеличению момента и скорости аппарата. Интересно, что никакими акселерометрами на борту зарегистрировать изменение скорости аппарата в маневрах невозможно, - они постоянно регистрируют состояние невесомости.

Преимущества гравитационного маневра по сравнению с гомановским перелетом к планетам-гигантам получаются настолько большими, что полезную нагрузку аппарата можно увеличить вдвое. Как уже говорилось, время достижения цели при гравитационном маневре у массивных планет-гигантов сокращается очень значительно. Разработка принципов маневра показала, что можно использовать и менее массивные тела (Землю, Венеру и, в особых случаях, даже Луну). Только масса в каком-то смысле разменивается на время полета, что заставляет исследователей ждать 2-3 лишних года. Однако стремление сократить расходы на дорогостоящие космические программы заставляет смириться с такой потерей времени. Теперь выбор трассы полета делается, как правило, многоцелевым, охватывающим несколько планет. В 1986 году гравитационный маневр у Венеры позволил обеспечить встречи советских аппаратов ВЕГА-1 и ВЕГА-2

с кометой Галлея.

Вояджер , Галилей и Кассини"

Рис. 2. Спутник Урана Миранда. Снимок аппарата Вояджер-2 .

Исключительно успешной была миссия аппаратов Вояджер , выполненная с использованием гравитационных маневров. Основные результаты исследований планет-гигантов и их спутников получены именно с помощью Вояджеров . На рис. 2 приведен снимок одного из самых необычных тел в Солнечной системе - спутника Урана Миранды, сделанный Вояджером-2 в январе 1986 г. Аппараты были запущены в США осенью 1977 г. и достигли первой цели миссии, планеты Юпитер, в 1979 г. После выполнения исследовательской программы у Юпитера и подробных исследований его спутников аппараты совершили гравитационный маневр (с использованием поля тяготения Юпитера), что позволило направить их по несколько различающимся траекториям к Сатурну, которого они достигли в 1980 и 1981 гг. соответственно. Здесь также изучались спутники и сама планета, но программа Вояджера-2 в последний момент была несколько сокращена из-за неполадок на борту. Далее Вояджер-1 выполнил сложный маневр, чтобы пройти на расстоянии всего 5000 км от Титана, спутника Сатурна, а затем оказался на траектории ухода из Солнечной системы. Вояджер-2 также проделал еще один гравитационный маневр и, несмотря на некоторые возникшие технические проблемы, был направлен к седьмой планете, Урану. Неисправности в ходе полета удалось, если не устранить, то обойти. Встреча с Ураном состоялась в начале 1986 г. После исследования Урана и его спутников Вояджер-2 сохранил работоспособность, чему значительно способствовало перепрограммирование его управляющих систем. Перепрограммирование было выполнено уже после запуска аппарата в результате большой работы специалистов, а также общего прогресса в прикладной математике, и осуществлялось с помощью радиокоманд. После сближения с Ураном снова был выполнен гравитационный маневр в его поле, и Вояджер-2 был направлен к Нептуну. Здесь гравитационный маневр позволил после Нептуна сблизиться достаточно тесно с его спутником Тритоном. Встречей с Нептуном в 1989 г. аппарат завершил планетную часть своей миссии. Теперь Вояджер-2 покидает Солнечную систему. Такой последовательный облет за сравнительно короткое время стал возможным благодаря гравитационным маневрам и случайному расположению планет-гигантов в относительно узком секторе неба. Повторение примерно такой же конфигурации произойдет лишь через 175 лет.

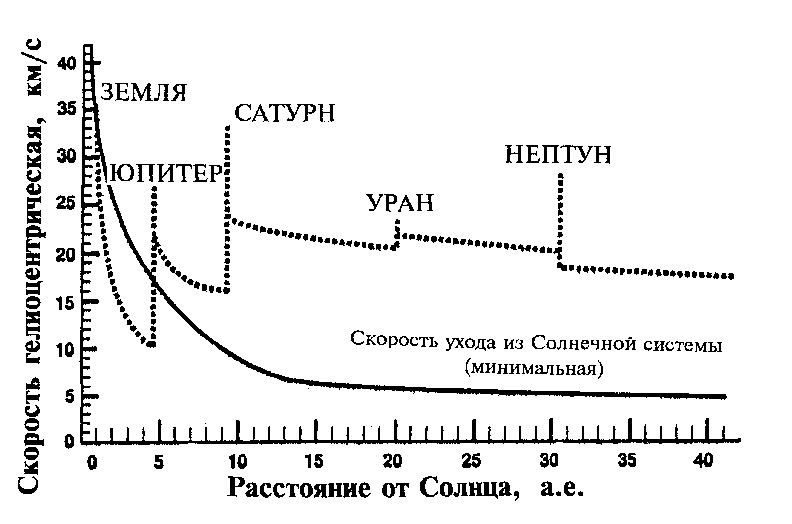
Рис. 3. Изменения скорости аппарата Вояджер-2 в ходе гравитационных маневров у планет-гигантов.

На рис. 3 показана вся динамика изменения скоростей аппарата Вояджер-2 . Сплошная линия показывает, как падает скорость аппарата без использования последовательности гравитационных маневров, пунктирная - реальные скорости аппарата. В случае Нептуна маневр был использован для уменьшения скорости, что понадобилось для достижения Тритона. На рисунке показаны также упоминавшиеся всплески скорости в сближениях. Как можно видеть, произошел выигрыш примерно в четыре раза в скорости за счет использования гравитационных маневров.

Рис. 4. Астероид Ида со спутником Дактиль. Снимок аппарата Галилей .

В самом конце 1995 г. Юпитера достиг новый аппарат, Галилей , трасса полета которого была выбрана как цепь гравитационных маневров в полях тяготения Земли и Венеры. Это позволило аппарату за 6 лет дважды посетить пояс астероидов и сблизиться с довольно крупными телами Гаспрой и Идой, да еще дважды вернуться к Земле. Схема полета аппарата Галилей показана на рис. 5. После запуска в США осенью 1989 г. аппарат был направлен к Венере, с которой сблизился в феврале 1990 г., а затем в декабре 1990 г. вернулся к Земле. Снова был выполнен гравитационный маневр, и аппарат ушел к внутренней части пояса астероидов, где в октябре 1991 г. провел съемку малой планеты Гаспра. Чтобы достичь Юпитера, в декабре 1992 г. Галилей снова вернулся к Земле и, наконец, лег на курс полета к Юпитеру. Во внешней части пояса астероидов в августе 1993 г. аппарат исследовал малую планету Ида (которая показана на рис. 4). Полет Галилея - пока самая сложная цепь гравитационных маневров. Выполнение планетной программы миссии Галилей несколько осложнилось техническими проблемами на борту аппарата, из-за чего передача информации возможна лишь в медленном режиме. Тем не менее, программа успешно выполняется. На рис. 6 показан сделанный Галилеем крупным планом снимок поверхности спутника Юпитера Европа.

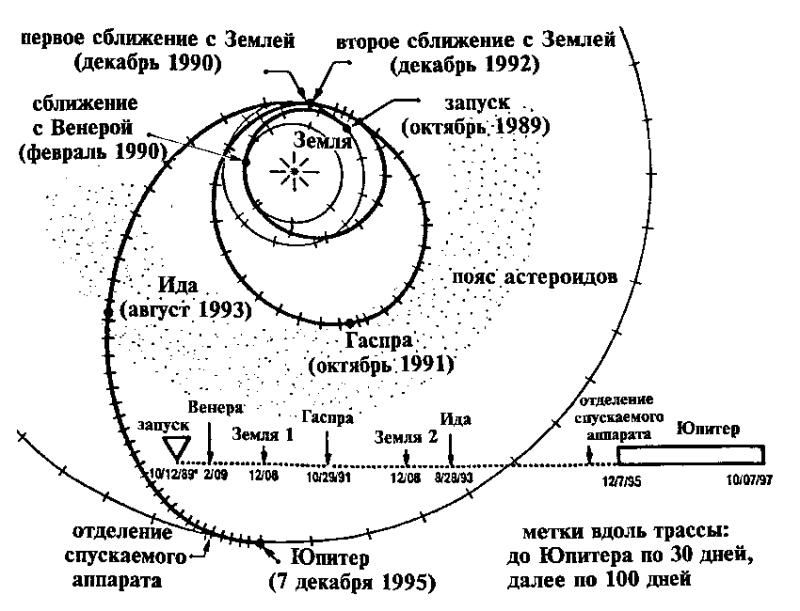
Рис. 5. Схема полета аппарата Галилей с большим числом гравитационных маневров.

В октябре 1997 г., также в США, к Сатурну был запущен аппарат Кассини . Программа его полета предусматривает четыре гравитационных маневра, два у Венеры и по одному у Земли и Юпитера (рис. 7). После первого маневра в сближении с Венерой (в апреле 1998 г.) аппарат уходит к орбите Марса и снова (без участия Марса) возвращается к Венере. Второй маневр у Венеры (июнь 1999 г.) возвращает Кассини к Земле. Здесь также выполняется гравитационный маневр (август 1999 г.). Так аппарат набирает достаточную скорость для быстрого полета к Юпитеру, где в конце декабря 2000 г. выполняется следующий, последний, маневр на пути к Сатурну. Цели аппарат должен достичь в июле 2004 г.

Рис. 6. Поверхность спутника Юпитера Европа.

Снимок аппарата Галилей .

 

Вероятно, в будущем использование гравитационных маневров станет еще более сложным. Как энтузиаст многократного использования гравитационных маневров выступает В.Г.Сурдин. Он считает, что достаточно сложная серия таких маневров позволит так разогнать космический аппарат, что его можно отправить за пределы Солнечной системы, к звездам, причем проект не потребует немыслимых затрат. Что же касается многих десятков или даже сотен лет, необходимых только на разгон, то по сравнению с длительностью самого полета это пренебрежимо малая величина. Добавим, что звездная миссия стала бы подарком от нас нашим очень далеким потомкам: только они могли бы воспользоваться результатами такого проекта, если бы он оказался успешным. Ныне аппараты Пионер-10 , Пионер-Сатурн , Вояджер-1 и Вояджер-2 навсегда уходят из Солнечной системы. Ожидается, что в 8571 году аппарат Вояджер-2 будет на расстоянии 0.42 светового года от Солнца и в 4 световых годах от звезды Барнарда. В 20 319 году он пройдет на минимальном расстоянии 3.5 световых года от звезды Проксима Центавра. А в 296 036 году он приблизится к Сириусу на расстояние 3.5 световых года...

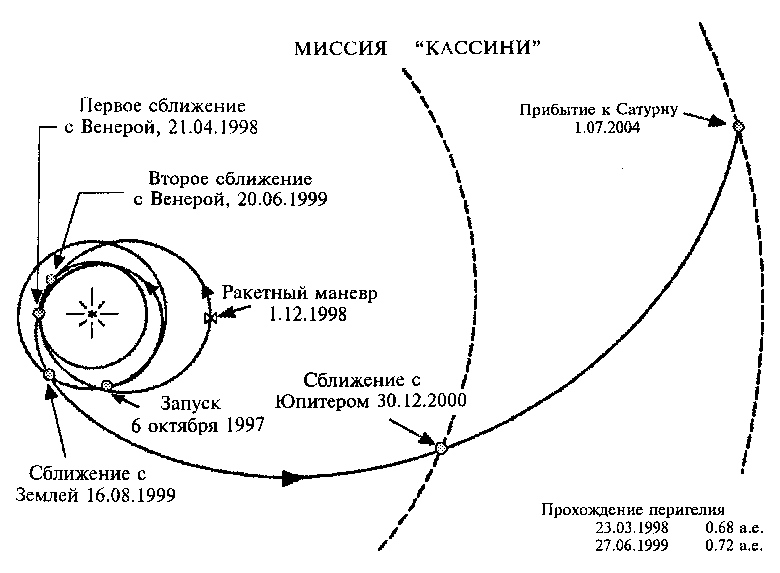
Рис. 7. Схема полета аппарата Кассини , запущенного к Сатурну в 1997 г.