 Они танцуют на орбитах
Они танцуют на орбитах12.03.2003 19:00 | М. Е. Прохоров/ГАИШ, Москва
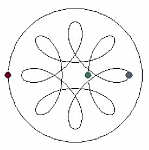
Классическая ньютоновская задача 3-тел еще не решена. Что уже говорить о более общей задаче n-тел в небесной механике. Одним из интересных и красивых направлений их исследования является поиск периодических решений - ситуаций, когда каждое из тел движется по замкнутой траектории и спустя некоторое время все они одновременно возвращаются в исходные точки.
Астрономы хорошо знают два семейства периодических Лагранжевых решений для системы из 3 тел - линейные, когда все тела расположены на одной прямой и треугольные - когда они в каждый момент времени образуют правильный треугольник. А какие конфигурации вы знаете еще?
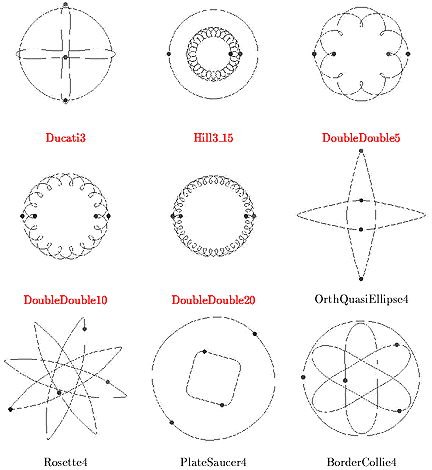
Роберт Вандербей (Robert Vanderbei) предложил способ поиска таких траекторий (см. astro-ph/0303153). Вот некоторые из них: названия конфигураций носят "мнемонический" характер, цифра в конце в большинстве случаев указывает на число тел. Красным цветом выделены названия устойчивых систем.
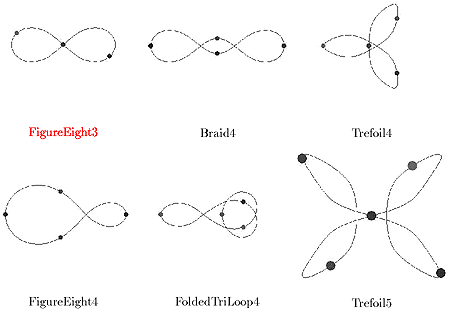
Частным случаем подобных орбит являются так называемые хореографии - конфигурации в которых все тела движутся по одной и той же траектории и равномерно распределены на ней. Таких конфигураций также удалось найти достаточно много, но устойчивой среди них оказалась только одна (и только для 3 тел равной массы) - известная ранее FigureEight3.
Кое-что еще по данной теме вы сможете найти на домашней странице автора статьи.
|
Публикации с ключевыми словами:
Небесная механика - задача n-тел
Публикации со словами: Небесная механика - задача n-тел | |
См. также:
Все публикации на ту же тему >> | |