Клод Шеннон: Математическая теория связи
<< Титульный лист | Оглавление | Часть 1. Дискретные системы без шума >>
Введение
Недавнее развитие различных методов модуляции, таких как PCM или PPM, основанных на улучшении пропускной способности за счет уменьшения отношения ``сигнал-шум'', привело к возрастанию интереса к общей теории связи. Основы такой теории заложены в важных статьях Найквиста (Nyquist, H., ``Certain Factors Affecting Telegraph Speed,'' Bell System Technical Journal, April 1924, p. 324; ``Certain Topics in Telegraph Transmission Theory,'' A.I.E.E. Trans., v. 47, April 1928, p. 617.) и Хартли(Hartley, R. V. L., ``Transmission of Information,'' Bell System Technical Journal, July 1928, p. 535.). В настоящей статье мы расширим эту теорию, учтя некоторое количество новых факторов, в частности - наличие шума в канале, а также статистическую структуру исходного сигнала и природу конечного приемника информации.
Основной задачей связи является восстановление (точное или приближенное) в данной точке сигнала, отправленного в другой. Часто сигнал имеет некое значение, то есть соотносится или коррелирует с заданными состояниями некоторой системы. Однако эти семантические аспекты связи не имеют отношения к инженерной задаче, важно лишь то, что сообщение выбирается из некоторого набора возможных. Система связи должна одинаково хорошо работать со всеми возможными вариантами сообщения, а не только с тем, который будет выбран в действительности - на этапе разработки системы это еще неизвестно.
Если набор содержит конечное число сообщений, то само это число или любая его монотонная функция может служить мерой информации, получаемой при выборе одного из них, если мы примем все варианты равновероятными. Как было отмечено Хартли, наиболее естественно выбрать логарифмическую функцию. И хотя это определение должно быть существенно обобщено на случаи неравновероятных сообщений и их непрерывных множеств, мы во всех случаях будем использовать именно логарифмические меры.
Логарифмическая мера удобна по следующим причинам:
- Она удобна практически. Параметры, важные в инженерных приложениях, такие как время, пропускная способность, число переключателей и так далее обычно меняются линейно при логарифмическом изменении числа возможных вариантов. К примеру, добавление одного переключателя удваивает число возможных состояний их группы, увеличивая на единицу его логарифм по основанию 2. Увеличение в два раза времени приводит к квадратичному росту числа сообщений, или удвоению их логарифма, и так далее.
- Она близка к нашему интуитивному представлению о такой мере. Это тесно связано с предыдущим пунктом, так как мы интуитивно измеряем величины, линейно сравнивая их со стандартами. Так, нам кажется, что на двух перфокартах можно разместить в два раза больше информации, а по двум одинаковым каналам - передать ее в два раза больше.
- Она удобна математически. Многие предельные переходы просты в логарифмах, в то время как в терминах числа вариантов они достаточно нетривиальны.
Выбор основания логарифма соответствует выбору единицы измерения информации.
Если взять основание 2, то полученные единицы можно назвать ``двоичными цифрами'',
или битами (binary digits -> bits, слово предложено Дж.В.Таки, J.W.Tukey)
Устройство с двумя устойчивыми состояниями, такое как переключатель или
триггер, способно хранить один бит информации, 
таких устройств
- бит, так как полное число состояний 
и
. При использовании же основания 10 единицы можно
назвать ``десятичными цифрами''. Так как ,
десятичная цифра примерно соответствует 
бит. Цифровое
колесо арифмометра имеет 10 устойчивых состояний, и потому может хранить одну
десятичную цифру информации. В аналитических расчетах, при проведении дифференцирования
и интегрирования, бывает полезно использовать натуральный логарифм, то есть
основание 
. Соответствующие единицы информации можно назвать
натуральными. Переход от основания 
к 
сводится
к умножению на 
.
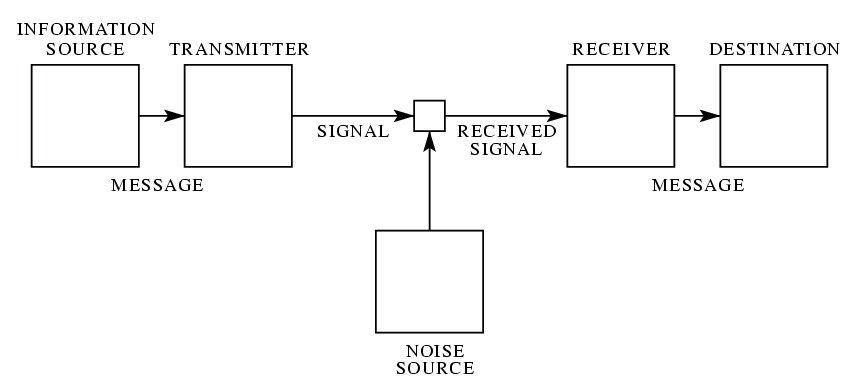
Рис. 1. Схематическое изображение общей системы связи.
Под системой связи мы будем понимать систему типа изображенной на рис.1. Такая система состоит из 5 частей:
-
Источника информации, испускающего сообщение или серию сообщений для
связи с приемной станцией. Сообщения могут быть различных типов: (а)
последовательностью букв, как в телеграфной системе, (б) некоторой
функцией времени
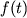, как в системе телефонной связи, (в)
функцией времени и других переменных, как в телевизионных системах - такое
сообщение можно рассматривать как функцию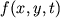 
двух пространственных
координат и времени, представляющую интенсивность излучения в точке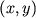 
в момент времени 
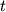на фотокатоде; (г) двумя или более
функциями времени, к примеру ,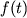 
, 
,
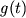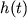как в случае передачи ``трехмерного звука'' или просто нескольких сигналов одновременно;
(д) несколькими функциями нескольких переменных - при передаче цветного телевизионного
сигнала мы имеем дело с тремя функциями ,
, 
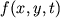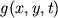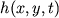, определенными на трехмерном
множестве (мы можем рассматривать три этих функции также как компоненты
трехмерного векторного поля в пространстве); кроме того, различные виды
сигналов могут возникать при передаче телевизионного изображения совместно со звуком
каналом.
- Передатчика, преобразующего неким образом сигнал и делающего его пригодным для передачи по линии связи. В телефонии это сводится главным образом к преобразованию давления звука в пропорциональный электрический сигнал. В случае телеграфа процесс кодирования сигнала преобразует его в последовательность точек, тире и пробелов в линии связи. В многоканальной PCM-системе различные функции различных голосов должны быть дискретизованы, сжаты, закодированы и, наконец, сведены надлежащим образом в один сигнал. Вокодеры (устройства цифрового кодирования речи), телевидение и частотная модуляция - другие примеры сложных преобразований, которым может быть подвергнуто сообщение при формировании сигнала.
- Канала, представляющего собой среду, используемую для передачи сигнала от передатчика к приемнику. Он может быть парой проводов, коаксиальным кабелем, радиоволнами определенной частоты, лучом света и т.д.
- Приемника, выполняющего задачи, противоположные выполняемым передатчиком, а именно - восстановления сообщения из сигнала.
- Пункта назначения - человека (или устройство), для которого сообщение предназначено.
Мы хотели бы рассмотреть некоторые общие задачи, имеющие отношение к системам связи. Для этого необходимо сначала представить различные вышеупомянутые элементы математическими величинами, отвлекаясь от их физической сущности. Системы связи можно грубо разделить на три категории: дискретные, непрерывные и смешанные. Под дискретной системой будем понимать такую, в которой и сообщение, и сигнал являются последовательностями дискретных символов. Типичным примером такой системы является телеграфия, в которой и сообщение, и сигнал являются последовательностями точек, тире и промежутков между ними. Непрерывная система - такая, в которой и сообщение, и сигнал рассматриваются как непрерывные функции, например, в радио или телевидении. В смешанной системе, соответственно, фигурируют как непрерывные, так и дискретные величины, как, например, в PCM-системе передачи речи.
Рассмотрим вначале дискретный случай. Он имеет приложения не только в теории связи, но также и в теории вычислительных машин и так далее. Вдобавок дискретные системы являются основой для рассмотрения непрерывных и смешанных, которые разбираются во второй половине статьи.
<< Титульный лист | Оглавление | Часть 1. Дискретные системы без шума >>
|
Публикации с ключевыми словами:
математика - информация - Шеннон
Публикации со словами: математика - информация - Шеннон | |
См. также:
Все публикации на ту же тему >> | |
