<< Суперсимметричные струны | Оглавление | Дуальность >>
Дополнительные измерения
Суперструны существуют в 10-мерном пространстве-времени, в то время как мы живем в 4-мерном. И если суперструны описывают нашу Вселенную, нам необходимо как-то связать между собой два эти пространства. Для этого свернем 6 измерений до очень маленького размера. Если при этом размер компактного измерения окажется порядка размера струн (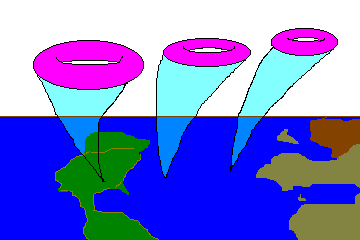
), то мы
из-за малости этого измерения попросту не сможем никак его напрямую увидеть. В конечном итоге мы получим наше
(3+1)-мерное пространство, в котором каждой точке нашей 4-мерной Вселенной отвечает крохотное
6-мерное пространство. Очень схематично это представлено на картинке снизу:
На самом деле это довольно старая идея, которая восходит к работам Калуцы (Kaluza) и Клейна (Klein) 1920-х годов. При этом описанный выше механизм называют теорией Калуцы-Клейна или компактификацией. В самой работе Калуцы показано, что если мы возьмем теорию относительности в 5-мерном пространстве-времени, затем свернем одно измерение в окружность, то получим 4-мерное пространство-время с теорией относительности плюс электромагнетизм ! А так получается из-за того, что электромагнетизм это U(1) калибровочная теория. U(1) это группа вращений вокруг точки на плоскости. Механизм Калуцы-Клейна дает простую геометрическую интерпретацию этой окружности - это то самое свернутое пятое измерение. Хотя свернутые измерения и малы для прямого детектирования, тем не менее они могут иметь глубокий физический смысл. [Совершенно случайно просочившись в прессу, работа Калуцы и Клейна вызвала много разговоров по поводу пятого измерения.]
Как мы сможем узнать, есть ли на самом деле дополнительные измерения и как мы сможем их
"почуствовать", имея ускорители с достаточно высокими энергиями ? Из квантовой механики известно,
что если пространство периодично, то импульс квантован: 
, тогда как
если пространство неограниченно, то спектр значений импульса непрерывен. Если уменьшать радиус
компактификации (размер дополнительных измерений), то диапазон дозволенных значений импульса будет
увеличиваться. Так получают башню состояний импульса - башню Калуцы Клейна.
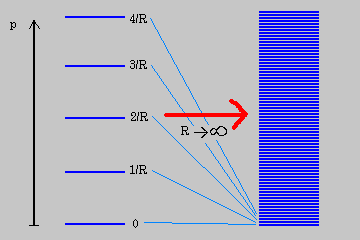
А если радиус окружности взять очень большим ("декомпактифицируем" измерение), то диапазон возможных значений импульса будет довольно узким, но будет "почти-непрерывным". Такой спектр будет похож на спектр масс мира без компактификаций. Например, безмассовые в большем числе измерений состояния в меньшем числе измерений будут выглядеть именно как описанная выше башня состояний. Тогда должен наблюдаться "набор" частиц с массами, равноотстоящими друг от друга. Правда, для того, чтобы "увидеть" самые массивные частицы, необходимы ускорители, значительно лучшие тех, которыми мы сейчас располагаем.
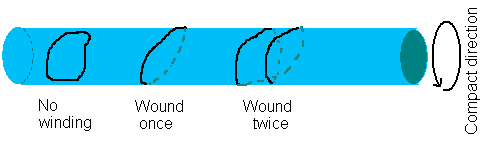
У струн есть еще одно замечательное свойство - они могут "наматываться" на компактифицированное
измерение, что приводит к появлению оборотных мод в спектре масс. Замкнутая струна может
обернуться вокруг компактифицированного измерения целое число раз. Аналогично случаю Калуцы-Клейна
они дают вклад в импульс как 
. Существенная разница состоит как раз
в другой связи с радиусом компактификации 
. В этом случае для малых размеров
дополнительных измерений оборотные моды становятся очень легкими !
Теперь нам необходимо перейти к нашему 4-мерному пространству. Для этого нам нужна 10-мерная суперструнная теория на 6-мерном компактном многообразии. Естественно, что при этом описанная выше картина становится более сложной. Проще всего положить, что все эти 6 измерений - 6 окружностей, таким образом все они представляют собой 6-мерный тор. Более того, такая схема позволяет сохранить суперсимметрию. Считается, что некоторая суперсимметрия существует и в нашем 4-мерном пространстве на энергетических масштабах порядка 1 ТэВ (именно на этих энергиях последнее время и ищут суперсимметрию на современных ускорителях). Для того, чтобы сохранить минимальную суперсимметрию, N=1 в 4-мерии, компактифицировать надо на специальном 6-мерном многообразии, именуемом многообразием Калаби-Йо (Calabi-Yau manifold).
Свойства многообразий Калаби-Йо могут иметь важные приложения к физике низких энергий - к частицам, которые мы наблюдаем, их массам и квантовым числам, а также к числу поколений частиц. Проблемой тут является то, что, вообще говоря, существует огромное множество многообразий Калаби-Йо, и мы не знаем, какое из них надо использовать. В этом смысле, имея фактически одну 10-мерную струнную теорию мы получаем, что 4-мерная теория становится совсем не единственно возможной, по крайней мере, на нашем (еще неполном) уровне понимания. "Струнные люди" (ученые, работающие в области струнных теорий) возлагают надежды на то, что обладая полной непертурбативной теорией струн (теорией, НЕ построенной на возмущениях, описанных несколько выше), мы сможем объяснить, как Вселенная перешла от 10-мерной физики, которая, возможно, имела место в течении высокоэнергетического периода сразу после Большого Взрыва, к 4-мерной, с которой мы имеем дело сейчас. [Иными словами, что мы найдем единственное многообразие Калаби-Йо.] Андрей Стромингер (Andrew Strominger) показал, что многообразия Калаби-Йо можно непрерывно связать друг с другом посредством конических преобразований (conifold transitions) и, таким образом, можно двигаться между различными многообразиями Калаби-Йо, меняя параметры теории. Но это предполагает возможность того, что различные 4-мерные теории, возникающие от различных многообразий Калаби-Йо, являются различными фазами одной теории.
<< Суперсимметричные струны | Оглавление | Дуальность >>
|
Публикации с ключевыми словами:
суперструны - супергравитация - квантовая гравитация - квантовая теория поля
Публикации со словами: суперструны - супергравитация - квантовая гравитация - квантовая теория поля | |
См. также:
Все публикации на ту же тему >> | |
