1.6. Трудный выбор системы координат
Земная опорная система координат закреплена набором прямоугольных координат сети
станций наблюдений, заданных на какую-либо дату. Геодезические широта ![]() , долгота
, долгота ![]() и высота пункта
и высота пункта ![]() с помощью экваториального радиуса Земли
с помощью экваториального радиуса Земли
![]() метров и сжатия Земли
метров и сжатия Земли
![]() связаны с координатами
связаны с координатами ![]() ,
, ![]() ,
, ![]() формулами
формулами
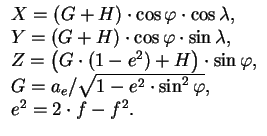
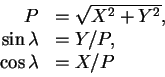
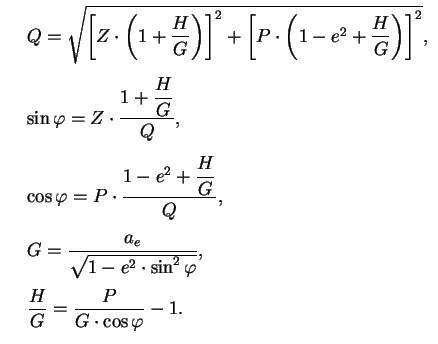
Небесная опорная система координат (ICRS) построена на основе высокоточных экваториальных положений 608 внегалактических радиоисточников.
Преобразование из земной системы на момент наблюдений![]() в небесную
выполняется по формуле
в небесную
выполняется по формуле
где ![]() и
и
![]() - векторы в земной и небесной опорной системах,
- векторы в земной и небесной опорной системах, ![]() -
матрица прецессии,
-
матрица прецессии,
![]() - матрица нутации,
- матрица нутации,
![]() - гринвичское истинное звездное
время,
- гринвичское истинное звездное
время, ![]() ,
, ![]() - координаты полюса. Верхний штрих означает транспонирование матрицы.
Обозначения
- координаты полюса. Верхний штрих означает транспонирование матрицы.
Обозначения
![]() ,
,
![]() ,
,
![]() введены для матриц поворота против часовой
стрелки на угол
введены для матриц поворота против часовой
стрелки на угол ![]() вокруг осей
вокруг осей ![]() ,
, ![]() ,
, ![]() .
.
Первой части формулы преобразования, произведению транспонированных матриц прецессии и нутации, соответствует движение Небесного Эфемеридного полюса, второй части соответсвуют вращение Земли и явление движения полюсов.
Представляется весьма естественным формулировать и решать задачи спутниковой геодинамики в системе истинного экватора даты: с земной опорной системой она связана второй частью формулы преобразования координат, а с небесной опорной системой - первой частью.
Это неинерциальная система отсчета, вращающаяся с переменной угловой скоростью
![]() , поэтому в уравнениях движения ИСЗ появятся силы инерции.
, поэтому в уравнениях движения ИСЗ появятся силы инерции.
С точностью до
первых степеней малых величин запишем
В выбранной системе будут вычисляться как координаты космических объектов, так и положения обсерваторий на моменты наблюдений. К этой же системе координат надо преобразовать выражения для возмущающих функций от всех действующих факторов.
В выражении для геопотенциала, например, необходимо учесть поправку к координате ![]()
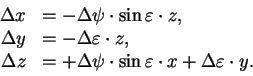
Преобразование от системы истинного экватора к горизонтальной системе после переноса начала
координат из центра Земли в пункт наблюдений выполняется с помощью двух поворотов: вокруг оси ![]() на угол
на угол
![]() , и вокруг оси
, и вокруг оси ![]() на угол
на угол
![]() . Геодезический азимут
отсчитывается от точки севера по часовой стрелке.
. Геодезический азимут
отсчитывается от точки севера по часовой стрелке.
<< 1.5. Метод чрезвычайно прост | Оглавление | 1.7. Параметры, которые определяют >>
|
Публикации с ключевыми словами:
астрометрия - лазерная локация
Публикации со словами: астрометрия - лазерная локация | |
См. также:
Все публикации на ту же тему >> | |