ИНФОРМАЦИЯ, ТЕРМОДИНАМИКА И КОНСТРУКЦИЯ БИОЛОГИЧЕСКИХ СИСТЕМ
Л.А.Блюменфельд (МГУ им. М.В.Ломоносова)Опубликовано в Соросовском образовательном журнале, N 7, 1996 г. Содержание
ИНФОРМАЦИЯ И ЭНТРОПИЯ
За 20 лет до появления работ Шеннона анализом информации занимался венгерский физик Сциллард [Szillard L., 1929] в связи с решением одного термодинамического парадокса, предложенного Максвеллом еще в прошлом веке [Maxwell J.C., 1971]. Смысл парадокса Максвелла заключается в следующем (рис. 1). Изолированная система, состоящая из разделенного на две части резервуара с газом и с дверцей в перегородке, содержит также "демона" (существо или автомат), наделенного способностью отличать быстрые молекулы от медленных. Демон открывает дверцу только в том случае, если к ней справа подлетает быстрая молекула. Поэтому газ в левой части резервуара будет нагреваться, а в правой - остывать. Таким образом, в изолированной системе тепло будет переходить от холодного тела к горячему с понижением энтропии системы в противоречии со вторым законом термодинамики.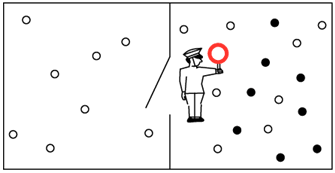 |
| Рис. 1. Демон Максвелла. |
| (3) |
где размерная постоянная Больцмана k = 1,38*10-16 эрг/град или 3,31*10-24 эе (эе - энтропийная единица, 1 эе = 1 кал/град). Рассчитаем, какое количество информации надо получить о системе, находящейся в данном макросостоянии, чтобы однозначно определить ее микросостояние. Иначе говоря, какого количества информации недостает для полного описания системы в заданном макросостоянии? Пусть микросостояние определено путем измерений или расчетов (на самом деле сделать это нельзя). До определения вероятность того, что макроскопическая система находилась именно в этом микросостоянии, была равна 1/W, а после определения стала равной единице. Полученное количество информации
| (4) |
Формулы (3) и (4) совпадают с точностью до постоянного размерного множителя. Величины I и S существенно идентичны. Ситуация здесь та же, что и для соотношения между массой и энергией: E = mc2, где роль размерного множителя играет с2. Аналогична ситуация и в случае соотношения между частотой и энергией кванта света, где размерным множителем является постоянная Планка:
| (5) |
|
Публикации с ключевыми словами:
информация - энтропия - термодинамика
Публикации со словами: информация - энтропия - термодинамика | |
|
См. также:
| |
Астрометрия
-
Астрономические инструменты
-
Астрономическое образование
-
Астрофизика
-
История астрономии
-
Космонавтика, исследование космоса
-
Любительская астрономия
-
Планеты и Солнечная система
-
Солнце