<< 1. Введение | Оглавление | 3. Системы небесных координат >>
2. Элементы геометрии на небесной сфере
Одной из важнейших астрономических задач, без которой невозможно решение всех остальных задач астрономии, является определение положения небесного светила на небесной сфере.
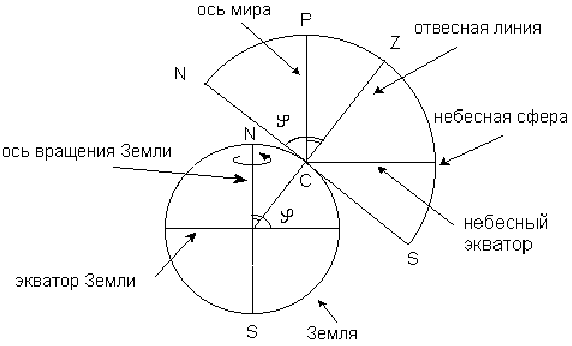
Небесная сфера - это воображаемая сфера произвольного радиуса, описанная из глаза наблюдателя, как из центра. На эту сферу мы проектируем положение всех небесных светил. Расстояния на небесной сфере можно измерять только в угловых единицах, в градусах, минутах, секундах или радианах. Например, угловые диаметры Луны и Солнца равны примерно 0.o5.
Одним из основных направлений, относительно которого определяется положение
наблюдаемого небесного светила, является отвесная линия. Отвесная
линия в любом месте земного шара направлена к центру тяжести Земли.
Угол между отвесной линией и плоскостью земного экватора называется
астрономической широтой ![]() .
.
В каждой точке Земли наблюдатель видит половину сферы, плавно вращающейся с востока на запад вместе с будто прикрепленными к ней звездами. Это видимое вращение небесной сферы объясняется равномерным вращением Земли вокруг своей оси с запада на восток.
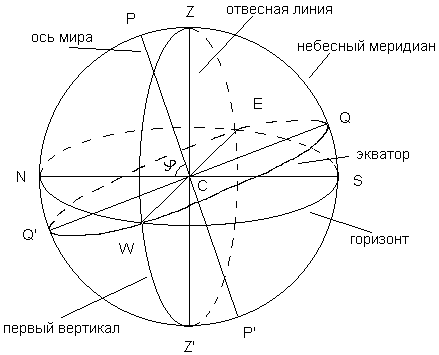
Отвесная линия пересекает небесную сферу в точке зенита, Z и в точке надира, Z'.
Большой круг небесной сферы, по которому горизонтальная плоскость, проходящая через глаз наблюдателя (точка С на рис.2), пересекается с небесной сферой, называется истинным горизонтом. Напомним, что большим кругом небесной сферы является круг, проходящий через центр небесной сферы. Круги, образованные пересечением небесной сферы с плоскостями, не проходящими через ее центр, называются малыми кругами.Линия, параллельная земной оси и проходящая через центр небесной сферы, называется осью мира. Она пересекает небесную сферу в северном полюсе мира, P, и в южном полюсе мира P'.
Из рис. 1 видно, что ось мира наклонена к плоскости истинного горизонта под
углом ![]() . Видимое вращение небесной сферы происходит вокруг оси мира
с востока на запад, в направлении, противоположном истинному вращению Земли,
которая вращается с запада на восток.
. Видимое вращение небесной сферы происходит вокруг оси мира
с востока на запад, в направлении, противоположном истинному вращению Земли,
которая вращается с запада на восток.
Большой круг небесной сферы, плоскость которого перпендикулярна оси мира, называется небесным экватором. Небесный экватор делит небесную сферу на две части: северную и южную. Небесный экватор параллелен экватору Земли.
Плоскость, проходящая через отвесную линию и ось мира, пересекает небесную сферу по линии небесного меридиана. Небесный меридиан пересекается с истинным горизонтом в точках севера, N , и юга, S. А плоскости этих кругов пересекаются по полуденной линии. Небесный меридиан является проекцией на небесную сферу земного меридиана, на котором находится наблюдатель. Поэтому на небесной сфере есть только один меридиан, ведь наблюдатель не может находиться на двух меридианах одновременно!
Небесный экватор пересекается с истинным горизонтом в точках востока, E , и запада, W. Линия EW перпендикулярна полуденной. Точка Q - верхняя точка экватора, а Q' - нижняя точка экватора.
Большие круги, плоскости которых проходят через отвесную линию, называются вертикалами. Вертикал, проходящий через точки W и E, называется первым вертикалом.
Большие круги, плоскости которых проходят через ось мира, называются кругами склонения или часовыми кругами.
Малые круги небесной сферы, плоскости которых параллельны небесному экватору, называются небесными или суточными параллелями. Суточными они называются потому, что по ним происходит суточное движение небесных светил. Экватор также является суточной параллелью.
Малый круг небесной сферы, плоскость которого параллельна плоскости горизонта, называется альмукантаратом.
Вопросы
1. Есть ли место на Земле, где вращение небесной сферы происходит вокруг отвесной линии?
Задачи
1. Изобразить на чертеже небесную сферу в проекции на плоскость горизонта.
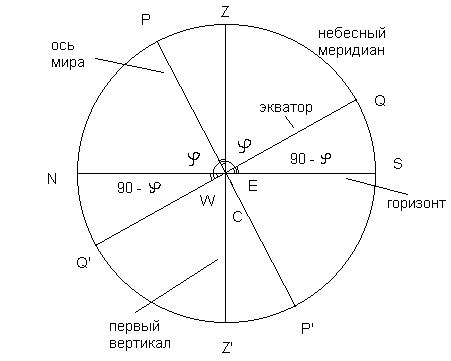
Решение: Как известно, проекцией какой-либо точки А на какую-либо плоскость является точка пересечения плоскости и перпендикуляра, опущенного из точки А к плоскости. Проекцией отрезка, перпендикулярного к плоскости, является точка. Проекцией круга, параллельного плоскости, является такой же круг на плоскости, проекцией круга, перпендикулярного к плоскости, является отрезок, а проекцией круга, наклоненного к плоскости, является эллипс, тем более сплюснутый, чем ближе угол наклона к 90o. Таким образом, для того, чтобы начертить проекцию небесной сферы на какую-либо плоскость, надо опустить на эту плоскость перпендикуляры из всех точек небесной сферы. Последовательность действий следующая. Прежде всего, необходимо начертить круг, лежащий в плоскости проекции, в данном случае это будет горизонт. Затем нанести все точки и линии, лежащие в плоскости горизонта. В данном случае это будет центр небесной сферы C, и точки юга S, севера N, востока E и запада W, а также полуденная линия NS. Далее опускаем перпендикуляры на плоскость горизонта из остальных точек небесной сферы и получаем, что проекцией зенита Z, надира Z' и отвесной линии ZZ' на плоскость горизонта является точка, совпадающая с центром небесной сферы C (см. рис. 3). Проекцией первого вертикала является отрезок EW, проекция небесного меридиана совпадает с полуденной линией NS. Точки, лежащие на небесном меридиане: полюса P и P', а также верхняя и нижняя точки экватора Q и Q' проецируются поэтому на полуденную линию тоже. Экватор является большим кругом небесной сферы, наклоненным к плоскости горизонта, поэтому его проекция - это эллипс, проходящий через точки востока E, запада W, и проекции точек Q и Q'.
2. Изобразить на чертеже небесную сферу в проекции на плоскость небесного меридиана.
Решение: Представлено на рис.4
3. Изобразить на чертеже небесную сферу в проекции на плоскость небесного экватора.
4. Изобразить на чертеже небесную сферу в проекции на плоскость первого вертикала.
<< 1. Введение | Оглавление | 3. Системы небесных координат >>
|
Публикации с ключевыми словами:
задача - общая астрономия - Небесная сфера - системы координат - суточное вращение - рефракция - Сумерки - время - движение планет - расстояние - звезды - галактика
Публикации со словами: задача - общая астрономия - Небесная сфера - системы координат - суточное вращение - рефракция - Сумерки - время - движение планет - расстояние - звезды - галактика | |
См. также:
Все публикации на ту же тему >> | |