Астронет > Механика сплошных сред

по текстам по ключевым словам в глоссарии по сайтам перевод по каталогу

Механика сплошных сред

Лекция 3

Стационарное течение жидкости. Уравнение Бернулли и его следствия. Понятие о дивергенции вектора. Условие несжимаемости. Уравнения Эйлера. Течение сжимаемых газов. Критерий несжимаемости. Распространение возмущений. Скорость звука. Сверхзвуковые потоки.

Стационарное одномерное течение несжимаемой жидкости.

Равновесие жидкостей и особенно газов, рассмотренное в предыдущей лекции, соответствует идеальным внешним условиям и поэтому на практике реализуется крайне редко. Обычно жидкости при внешнем воздействии приходят в движение, при этом давление и скорость ее частиц, вообще говоря, могут сложным образом меняться от точки к точке внутри объема текущей жидкости. Поясним сказанное примером. Подключим горизонтальную стеклянную трубку переменного сечения при помощи резинового шланга к водопроводному крану (рис. 3.1). Если напор воды остается постоянным, то течение воды можно считать установившимся (или стационарным). В этом случае масса воды M, протекающая в единицу времени через сечения с площадями S₁ и S₂ будет одинаковой, поэтому имеет место равенство

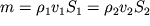$m = \rho_1 v_1 S_1 = \rho_2 v_2 S_2$

(3.1)

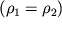
где ( $\rho$ и v - плотность и скорость жидкости в этих сечениях. Если жидкость несжимаема $(\rho_1 = \rho_2)$ , то условие (3.1) переходит в условие постоянства объема жидкости (условие несжимаемости), протекающего через сечения S₁ и S₂:

V = v₁S₁ = v₂S₂

(3.2)

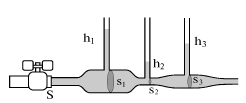Рис. 3.1.

Следует отметить, что условия постоянства массы (3.1) и несжимаемости жидкости (3.2) записаны для случая, когда скорости всех частиц жидкости одинаковы в поперечном сечении трубки. Для графического изображения течения жидкости удобно использовать линии тока - линии, касательная к которым в каждой точке совпадает с вектором скорости частицы (рис. 3.2). Легко видеть, что в сечении S скорости частиц различны, и объем протекающей жидкости через это сечение не может быть записан в виде (3.2).

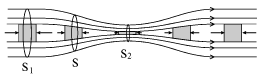Рис. 3.2.

Далее отметим, что по мере приближения к узкому сечению S₂ частица, деформируясь, ускоряется (в силу 3.2), а при удалении от S₂ - замедляется. Эти ускорения могут обеспечить лишь силы давления f_i = - p_in, показанные на рис. 3.2 маленькими стрелками. Из рисунка ясно, что давление в жидкости по мере приближения к S₂ падает. А затем возрастает. Это легко проверить, если сравнить уровни h₁ и h₂ жидкости в манометрических стеклянных трубках, впаянных в горизонтальную трубку вблизи сечений S₁ и S₂. 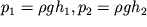Поскольку $p_1 = \rho g h_1, p_2 = \rho g h_2$ , то p₁ > p₂, т.к. h₁> ;h₂. На рис. 3.3 качественно изображено распределение скоростей и давлений вдоль оси трубки (см. рис. 3.2).

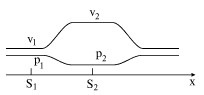Рис. 3.3.

Для количественного описания течения жидкости разобьем поток жидкости по трубе на элементарные потоки по воображаемым трубкам тока, образуемых семейством линий тока. В поперечном сечении трубки тока скорость частиц приблизительно одинакова, и это обстоятельство существенно облегчаем анализ течения жидкости. Найдем количественную связь между скоростью и давлением, качественно отображенную на рис. 3.3. При прямолинейном течении частиц воды вдоль осевой трубки тока сумма сил, приложенных к единице объема (см. 2.5), обеспечивают его ускорение. В соответствии со 2-м законом Ньютона можно записать

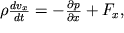$\rho\frac{dv_x}{dt} = -\frac{\partial p}{\partial x} + F_x,$

(3.3)

где F_x - плотность, имеющая размерность Н/м³. Отметим, что в уравнение (3.3) не входят силы вязкости, зависящие от скорости движения элемента жидкости. Впоследствии мы учтем их влияние и выясним условия, при которых ими можно пренебречь. Изменение скорости частицы dv_x и связанное с ним ускорение может происходить как вследствие стационарного движения частицы от широкого к узкому (или наоборот) сечению, так и при нестационарном изменении скорости течения во времени (например, при медленном увеличении или ослаблении напора воды с помощью крана). Поэтому в общем случае скорость частиц является функцией не только координаты x, но и времени t:

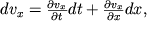$dv_x = \frac{\partial v_x}{\partial t}dt + \frac{\partial v_x}{\partial x}dx,$

(3.4)

где dx=v_xdt - расстояние, пройденное частицей за время dt. Подставляя (3.4) в (3.3), приходим к уравнению Эйлера

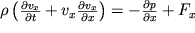$\rho \left( \frac{\partial v_x}{\partial t} + v_x \frac{\partial v_x}{\partial x}\right) = -\frac{\partial p}{\partial x} + F_x$

(3.5)

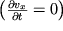
описывающее одномерное течение несжимаемой невязкой жидкости. При стационарном течении жидкости по горизонтальной трубе скорость не зависит от времени $\left( \frac{\partial v_x}{\partial t} =0 \right)$ , внешние силы F_x=0, и уравнение Эйлера принимает простой вид

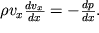
$\rho v_x \frac{dv_x}{dx}=-\frac{dp}{dx}.$

(3.6)

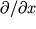
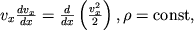
Здесь вместо $\partial / \partial x$ используется символ полной производной d/dx. Учитывая, что $v_x \frac{dv_x}{dx}=\frac{d}{dx}\left( \frac{v_x^2}{2} \right), \rho = {\rm const},$ перепишем (3.6) в виде

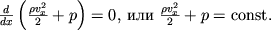
$\frac{d}{dx}\left( \frac{\rho v_x^2}{2} + p \right)=0$, или $\frac{\rho v_x^2}{2} + p = {\rm const}.$

(3.7)

Равенство (3.7), устанавливающее связь между давлением и скоростью, является частным случаем уравнения Бернулли. Константа, входящая в это уравнение, определяется из значений давления и скорости в каком-либо сечении трубки тока. Используя это уравнение, определим массу воды (расход), проходящую за единицу времени через сечение трубки, изображенной на рис. 3.2. В соответствии с уравнением (3.7) давления и скорости в сечениях S₁ и S₂ связаны соотношением

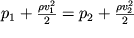
$p_1 + \frac{\rho v_1^2}{2}=p_2 + \frac{\rho v_2^2}{2}$

(3.8)

Помимо этого, искомый расход воды определяется равенством (3.1):

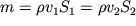
$m=\rho v_1 S_1= \rho v_2 S_2$

(3.9)

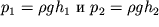
Поскольку давление $p_1 = \rho g h_1$ и $p_2 = \rho g h_2$ и определяются по показаниям h₁ и h₂ манометрических трубок, то решая систему уравнений (3.8) и (3.9) относительно m, находим

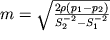
$m=\sqrt{\frac{2\rho (p_1 - p_2)}{S_2^{-2} - S_1^{-2}}}$

(3.10)

Для измерения расхода воды на практике применяются водомеры, основу которых составляет труба переменного сечения, оснащенная манометрами для измерения давлений p₁ и p₂ в известных сечениях S₁ и S₂.

Течение жидкости в поле силы тяжести. Уравнение Бернулли.

Рассмотрим задачу о течении жидкости вдоль произвольных трубок тока, могущих составлять произвольный переменный угол с горизонтом. Одна из наших криволинейных трубок показана на рис. 3.4. Если ввести криволинейную координату $\ell$ , совпадающую с осью трубки тока, то при стационарном течении жидкости ее скорость и давление являются функциями этой координаты. Проектируя силу тяжести на ось $\ell$ , запишем уравнение Эйлера (3.5) в виде:

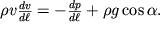
$\rho v \frac{dv}{d\ell}=- \frac{dp}{d\ell}+ \rho g \cos \alpha.$

(3.11)

Здесь v - скорость частиц, направленная вдоль оси трубки.

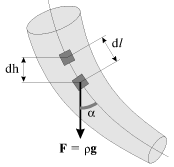Рис. 3.4.

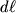
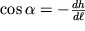
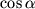
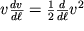
Если элемент жидкости сместился вниз на расстояние $d\ell$ , то он сместился (опустился) на высоту dh<0, при этом $\cos \alpha= - \frac{dh}{d\ell}$ . Подставляя значение $\cos \alpha$ в (3.11) и используя тождество $v\frac{dv}{d\ell}=\frac{1}{2}\frac{d}{d\ell}v^2$ , находим

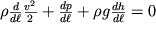
$\rho \frac{d}{d\ell}\frac{v^2}{2}+\frac{dp}{d\ell}+\rho g \frac{dh}{d\ell} =0$

(3.12)

Для несжимаемой жидкости $\rho$ =const, и последнее равенство трансформируется к виду

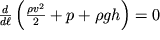
$\frac{d}{d\ell}\left(\frac{\rho v^2}{2} +p + \rho gh \right) =0$

(3.13)

Интегрируя (3.13) вдоль трубки тока, получаем уравнение Бернулли

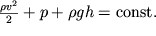
$\frac{\rho v^2}{2}+p+\rho gh = {\rm const}.$

(3.14)

Это уравнение описывает стационарное течение несжимаемой жидкости (иногда употребляют термин "идеальной жидкости"), и играет фундаментальную роль в гидродинамических исследованиях. Если нам известно давление p₁, скорость v₁ в некотором сечении трубки тока, находящемся на высоте h₁, то в любом другом сечении на высоте h величины p и v связаны соотношением

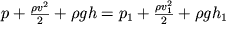
$p+\frac{\rho v^2}{2}+\rho gh = p_1+ \frac{\rho v_1^2}{2}+\rho gh_1$

(3.15)

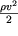
Давление p - это статическое давление, которое получит манометр, находящийся в жидкости и движущийся вместе с нею, $\frac{\rho v^2}{2}$ - это динамическое давление, смысл которого будет раскрыт позднее. Заметим, что в покоящейся жидкости равенство (3.15) описывает гидростатическое распределение давлений. Уравнение Бернулли может быть получено с использованием закона сохранения энергии. В отсутствие сил вязкости, приращение суммарной (потенциальной и кинетической) энергии массы воды, находящейся в трубке тока между сечениями S₁ и S₂ (рис. 3.5) равно работе сил давления. 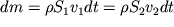Из рисунка видно, что за время dt течение жидкости эквивалентно по конечному результату перемещению элемента массой $dm=\rho S_1 v_1 dt= \rho S_2 v_2 dt$ с высоты h₁ на высоту h₂ и одновременному повышению его скорости от величины v₁ до величины v₂.

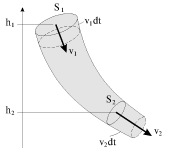Рис. 3.5.

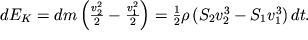
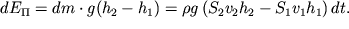
Приращение кинетической энергии равно: $dE_K=dm \left(\frac{v_2^2}{2} - \frac{v_1^2}{2}\right)=\frac{1}{2} \rho \left( S_2 v_2^3 -S_1 v_1^3 \right) dt.$ Приращение потенциальной энергии $dE_П=dm \cdot g (h_2 - h_1) = \rho g \left( S_2 v_2 h_2 -S_1 v_1 h_1\right) dt.$ Работа сил давления dA=p₁S₁v₁dt - p₂S₂v₂dt. Записывая уравнения энергетического баланса в виде dE_K+dE_П=dA, получаем уравнение Бернулли:

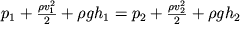
$p_1+\frac{\rho v_1^2}{2}+\rho gh_1 = p_2+ \frac{\rho v_2^2}{2}+\rho gh_2$

(3.16)

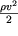
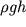
Проведенный энергетический вывод уравнения Бернулли делает более понятным физический смысл входящих в него членов. Так, статическое давление p численно равно работе сил давления, совершаемых над единичным объемом жидкости; динамическое давление $\frac{\rho v^2}{2}$ есть кинетическая энергия единицы объема, а величина $\rho gh$ является потенциальной энергией единичного объема в поле силы тяжести. Применим уравнение Бернулли к расчету течения жидкости в ряде интересных физических задач.

Назад | Вперед

Публикации с ключевыми словами: механика - гидродинамика - газодинамика - упругость Публикации со словами: механика - гидродинамика - газодинамика - упругость
См. также: Д'Аламбера-Эйлера парадокс Механика твердого тела. Лекции. Число Маха Вариационные принципы механики Конус Маха Бернулли уравнение Баротропное явление Все публикации на ту же тему >>

Мнения читателей [4]

Версия для печати

Астрометрия - Астрономические инструменты - Астрономическое образование - Астрофизика - История астрономии - Космонавтика, исследование космоса - Любительская астрономия - Планеты и Солнечная система - Солнце